Patterson, Bailey - Solid State Physics Introduction to theory

478 8 Superconductivity

The ac Josephson effect occurs if we apply a voltage difference V across the junction, so that qV with q = 2e is the energy change across the junction. The relevant equations become

Again, J0 is the maximum current carried by Cooper pairs. Additional current is carried by single-particle excitations producing the voltage V. The idea is shown later in Fig. 8.18. Therefore, since V is voltage in units of , the current oscillates with frequency (see (8.85))

For the dc Josephson effect one can say that for low enough currents there is a current across the insulator in the absence of applied voltage. In effect because of the coherence of Cooper pairs, the insulator becomes a superconductor. Above a critical voltage, Vc, one has single electrons and the material becomes ohmic rather than superconducting. The junction then has resistance, but the current also has a component that oscillates with frequency ωJ as above. One understands this by saying that above Vc one has single particles as well as Cooper pairs. The

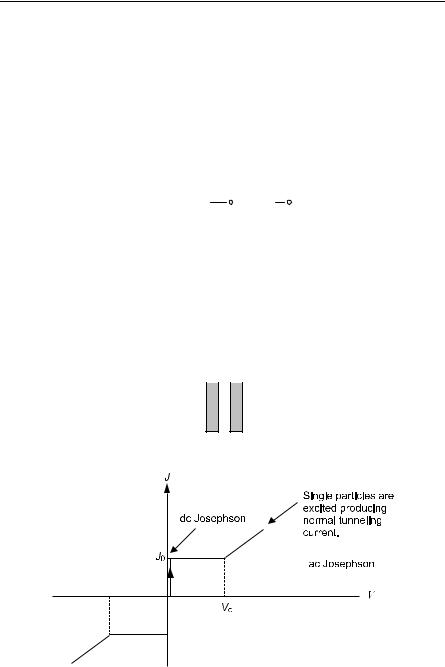
8.4 SQUID: Superconducting Quantum Interference (EE) 479

Cooper pairs change their energy by 2eV = ωJ as they cross the energy gap causing radiation at this frequency. The ac Josephson effect, which occurs when

is satisfied, is even more interesting. With q = 2e (for a Cooper pair), (8.87) is believed to be exact. Thus, the ac Josephson effect can be used for a precise determination of e/ . Parker, Taylor, and Langenberg6 have done this. They used their new value of e/ to determine a new and better value of the fine structure constant α. Their new value of α removed a discrepancy between the quantumelectrodynamics calculation and the experimental value of the hyperfine splitting of atomic hydrogen in the ground state. These experiments have also contributed to better accuracy in the determination of the fundamental constants. There have been many other important developments connected with the Josephson effects, but they will not be presented here. Reference [8.20] is a good source for further discussion. See also Fig. 8.18 for a summary.

Finally, it is worth pointing out another reason why the Josephson effects are so interesting. They represent a quantum effect operating on a macroscopic scale. We can play with words a little, and perhaps convince ourselves that we understand this statement. In order to see quantum effects on a macroscopic scale, we must have many particles in the same state. For example, photons are bosons, and so, we can obtain a large number of them in the same state (which is necessary to see the quantum effects of electrons on a large scale). Electrons are fermions and must obey the Pauli principle. It would appear, then, to be impossible to see the quantum effects of electrons on a macroscopic scale. However, in a certain sense, the Cooper pairs having total spin zero, do act like bosons (but not entirely; the Cooper pairs overlap so much that their motion is highly correlated, and this causes their motion to be different from bosons interacting by a two-boson potential). Hence, we can obtain many electrons in the same state, and we can see the quantum effects of superconductivity on a macroscopic scale.

8.4 SQUID: Superconducting Quantum Interference (EE)

A Josephson junction is shown in Fig. 8.17 below. It is basically a superconduc- tor–insulator–superconductor or a superconducting “sandwich”. We now show how flux, due to B, threading the circuit can have profound effects. Using (8.4) with φ the Ginzburg–Landau phase, we have

6 See [8.24].

480 8 Superconductivity

Fig. 8.17. A Josephson junction

Fig. 8.18. Schematic of current density across junction versus V. The Josephson current 0 < J < J0 occurs with no voltage. When J > J0 at Vc Eg/e, where Eg is the energy gap, one also has single-particle current

482 8 Superconductivity

A. If the insulator is much thinner than the coherence length, the superconducting pairs of electrons tunnel right through, and the insulator does not interfere with them–it is just one superconductor.

Q2. What is the simplest way to understand the ac Josephson effect (a current with a component of frequency 2eV/ , where V is the applied voltage)?

A. The Cooper pairs have charge q = 2e, and when they tunnel across the insulator, they drop in energy by qV. Thus they radiate with frequency qV/ . This radiation is linked to the ac current.

8.5 The Theory of Superconductivity 7 (A)

8.5.1Assumed Second Quantized Hamiltonian for Electrons and Phonons in Interaction (A)

As has already been mentioned, in many materials the superconducting state can be accounted for by an attractive electron–electron interaction due to the virtual exchange of phonons. See, e.g., Fig. 8.19. Thus, if we are going to try to understand the theory of superconductivity from a microscopic viewpoint, then we must examine, in detail, the nature of the electron–phonon interaction. There is no completely rigorous road to the BCS Hamiltonian. The arguments given below are intended to show how the physical origins of the BCS Hamiltonian could arise. It is not claimed that this is the way it must arise. However, given the BCS Hamiltonian, it is fair to say that the way it describes superconductivity is well understood.

One could draw an analogy to the Heisenberg Hamiltonian. The road to this Hamiltonian is also not rigorous for real materials, but there seems to be no doubt that it well describes magnetic phenomena in at least certain materials. The phenomena of superconductivity and ferromagnetism are exact, but the road to a quantitative description is not.

We thus start out with the Hamiltonian, which represents the interaction of electrons and phonons. As before, an intuitive approach suggests

We have already discussed this Hamiltonian in Chap. 4, which the reader should refer to, if needed. By the theory of lattice vibrations, we also know that (see Chaps. 2 and 4)

7 See Bardeen et al [8.6].

484 8 Superconductivity

We can now write the total Hamiltonian for interacting electrons and phonons (with = 1, and neglecting the zero-point energy of the lattice vibrations):

where the first two terms are the unperturbed Hamiltonian H0.

The first term is the Hamiltonian for phonons only (with nq = a†qaq as the phonon occupation number operator). The second term is the Hamiltonian for electrons only (with nk = C†kCk as the electron occupation number operator). The third term represents the interaction of phonons and electrons. We have in mind that the second term really deals with quasielectrons. We can assign an effective mass to the quasielectrons in such a manner as partially to take into account the electron– electron interactions, electron interactions with the lattice, and at least partially any other interactions that may be important but only lead to a “renormalization” of the electron mass. Compare Sects. 3.1.4, 3.2.2, and 4.3, as well as the introduction in Chap. 4. We should also include a screened Coulomb repulsion between electrons (see Sect. 9.5.3), but we neglect this here (or better, absorb it in Vk,k′—to be defined later).

Various experiments and calculations indicate that the energy per atom between the normal and superconducting states is of order 10−7 eV. This energy is very small compared to the accuracy with which we can hope to calculate the absolute energy. Thus, a frontal attack is doomed to failure. So, we will concentrate on those terms leading to the energy difference. The rest of the terms can then be pushed aside. The results are nonrigorous, and their main justification is the agreement we get with experiment. The method for separating the important terms is by no means obvious. It took many years to find. All that will be done here is to present a technique for doing the separation.

The technique for separating out the important terms involves making a canonical transformation to eliminate off-diagonal terms of O(Bq) in the Hamiltonian. Before doing this, however, it is convenient to prove several useful results. First, we derive an expansion for

486 8 Superconductivity

From XHep + [H0,S] = 0, we can calculate S. This is especially easy if we use a representation in which H0 is diagonal. In such a representation

The above equation determines the matrix elements of S and, hence, defines the operator S (for Em ≠ En).

8.5.2Elimination of Phonon Variables and Separation of Electron– Electron Attraction Term Due to Virtual Exchange of Phonons

(A)

Let us now connect the results we have just derived with the problem of superconductivity. Let XHep be the interaction Hamiltonian for the electron–phonon system. Any operator that we present for S that satisfies

is good enough. In the above equation, |m means both electron and phonon states. However, let us take matrix elements with respect to phonon states only and select S so that if we were to take electronic matrix elements, the above equation would be satisfied. This procedure is done because the behavior of phonons, except insofar as it affects the electrons, is of no interest. The point of this Section is then to find an effective Hamiltonian for the electrons.

We begin with these ideas. Taking phonon matrix elements, we have