
Теорія ймовірності - high_math
.pdfD( X ) = M (X 2 ) − [M (X )]2 . |
(2.17) |
Квадрат випадкової величини X , заданої рядом розподілу (2.1), |
|
є випадкова величина X 2 , яка набуває можливих значень xi2 |
з імо- |
вірностями pi ( i = 1, 2, ..., n ), оскільки, як тільки випадкова величина X набуває певного можливого значення, наприклад x1 , величина
X 2 набуває можливого значення x12 . Тому для обчислення дисперсії дискретної випадкової величини X , крім формули (2.15), застосовують формулу:
n
D(X ) = ∑ xi2 pi − [M (X )]2
i=1
і, відповідно, для неперервної випадкової величини, крім формули
(2.16), формулу:
b |
|
D(X ) = ∫ x2 f (x)dx − [M (X )]2 . |
(2.18) |
a
Якщо неперервна випадкова величина задана щільністю ймовірності f (x) при x (−∞;∞) , то
∞
D(X ) = ∫ x2 f (x)dx − [M (X )]2 .
−∞
Приклад 2.8. Випадкова величина X — кількість надійних приладів у системі, розглянута в прикладі 2.1, має такий ряд розподілу:
Х |
0 |
1 |
2 |
3 |
|
|
|
|
|
Р |
0,006 |
0,092 |
0,398 |
0,504 |
Знайти дисперсію D(X ).
Розв’язання. За означенням математичного сподівання маємо:
M (X ) = 1 0,092 + 2 0,398 + 3 0,504 = 2,4,
M (X 2 ) = 1 0,092 + 4 0,398 + 9 0,504 = 6,22 .
За формулою (2.17) дістаємо:
D(X ) = 6,22 − (2,4)2 = 0,46 .
81

Приклад 2.9. Неперервну випадкову величину X задано щільні-
стю ймовірності |
|
x (1; e); |
ln x |
ï ðè |
|
f (x) = {0 |
ï ðè |
x (1; e). |
Знайти дисперсію D(X ) .
Розв’язання. Знову застосуємо формулу (2.17). Математичне сподівання випадкової величини Х та її квадрата знаходимо за формулою (2.12), інтегруючи частинами:
M (X ) = ∫e |
x ln xdx = |
1 |
(e2 |
+ 1) |
, M (X 2 ) = ∫e |
x2 ln xdx = |
2e3 + 1 |
. |
||||||
4 |
9 |
|||||||||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тоді |
|
|
2e3 + 1 |
|
|
|
|
|
|
|
|
|||
|
D(X ) = |
|
− |
|
1 |
(e2 |
+ 1)2 ≈ 0,176 . |
|
|
|||||
|
|
|
16 |
|
|
|||||||||
|
|
|
|
9 |
|
|
|
|
|
|
|
|||
Наведемо властивості дисперсії.
1.Дисперсія сталої величини C дорівнює нулю: D(C) = 0.
2.Сталу величину C можна виносити за знак дисперсії, піднося-
чи її до квадрата: D(CX ) = C2 D( X ) .
3.Дисперсія суми n незалежних випадкових величин X1, X2 , ..., Xn дорівнює сумі їхніх дисперсій:
D( X1 + X2 + ... + Xn ) = D( X1 ) + D( X2 ) + ... + D( Xn ).
4.Дисперсія суми випадкової величини X і сталої величини C дорівнює дисперсії випадкової величини X : D(X + C) = D(X ).
5.Дисперсія різниці двох незалежних випадкових величин X і Y дорівнює сумі їхніх дисперсій: D(X − Y ) = D(X ) + D(Y ).
Зауваження. Поширення властивостей 3 і 5 дисперсії на залежні випадкові величини буде виконано у темі4 цього модуля.
Ще однією характеристикою розсіяння випадкової величини є
середнє квадратичне відхилення. Оскільки за означенням диспер-
сія має розмірність квадрата випадкової величини, то для характеристики розсіяння зручніше застосовувати арифметичне значення квадратного кореня з дисперсії. Ця величина називається
82

середнім квадратичним відхиленням випадкової величини і по-
значається σ(X ) :
σ(X ) = D(X ).
Приклад 2.10. Дискретну випадкову величину задано таким рядом розподілу:
|
Х |
– 0,1 |
x2 |
|
0,2 |
0,4 |
|
|
|
|
|
|
|
|
|
|
Р |
0,3 |
0,1 |
|
p3 |
p4 |
|
Знайти x2 , p3 , |
p4 , якщо відомі математичне сподівання М(Х) = 0,13 |
||||||
і дисперсія D(X ) = 0,0341. Скласти функцію розподілу F(х) випадко-
вої величини Х та знайти ймовірність потрапляння цієї випадкової величиниу проміжок(–0,05; 0,2].
Розв’язання. За умовою (2.2) для ряду розподілу: 0,3 + 0,1+ p3 + p4 = 1 або p4 = 0,6 − p3.
За означенням математичного сподівання:
M (X ) = −0,03 + 0,1x2 + 0,2 p3 + 0,4(0,6 − p3 ) = 0,13,
звідки дістаємо перше рівняння для знаходження x2 і p3 :
0,1x2 − 0,2 p3 = −0,08 .
За формулою (2.17) для дисперсії
D(X ) = 0,003 + 0,1x22 + 0,04 p3 + 0,16(0,6 − p3 )− (0,13)2 = 0,0341,
звідки дістаємо друге рівняння:
0,1x22 − 0,12 p3 = −0,048.
Система рівнянь |
0,1x |
|
− 0,2 p |
|
= −0,08, |
||
|
2 |
|
|
3 |
|
= −0,048 |
|
|
0,1x |
2 |
− 0,12 p |
3 |
|||
|
|
2 |
|
|
|
|
|
має розв’язки: x2 = 0, p3 = 0,4 і x2 |
2 |
= 0,6, p3 = 0,7, другий із яких не |
|||||
1 |
1 |
|
|
|
|
2 |
|
задовольняє умову задачі, оскільки не виконується обов’язкова вимога (2.2). Тому остаточно x2 = 0, p3 = 0,4, p4 = 0,2, і ряд розподілу набирає вигляду:
83
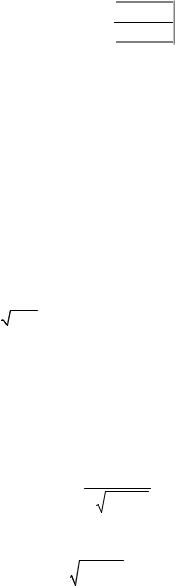
Х |
– 0,1 |
0 |
0,2 |
|
0,4 |
Р |
0,3 |
0,1 |
0,4 |
|
0,2 |
Функцію розподілу F (x) складемо згідно з формулою (2.4):
0,0,3,
F (x) = 0,4,
0,8,
1,
x ≤ −0,1, −0,1 < x ≤ 0, 0 < x ≤ 0,2, 0,2 < x ≤ 0,4, x > 0,4.
Імовірність того, що Х у результаті випробування набуде можливого значення з проміжку (–0,05; 0,2] обчислимо безпосередньо з ряду розподілу:
P{−0,05 < X ≤ 0,2} = P{ X = 0} + P{ X = 0,2} = 0,5.
Приклад 2.11. Неперервну випадкову величину Х задано функцією розподілу:
0, |
|
|
x ≤ 1, |
|
3 |
x − 1, |
1 < x ≤ 9, |
F (x) = A |
|
||
|
|
|
x > 9. |
1, |
|
|
Знайти: а) параметр А; б) щільність імовірності f (x); в) числові характеристики M(X), D(X), σ(X) ; г) імовірність того, що випадкова
величина Х у результаті випробування набуде можливого значення з інтервалу (1; 3).
Розв’язання. а) За властивістю 4 функції розподілу F(9) = 2A = 1,
звідки А = 1/2. |
1 |
|
|
|
б) Щільність імовірності: f (x) = F ′(x) = |
, |
x (1; 9). |
||
6 3 (x − 1)2 |
в) Математичне сподівання обчислюємо за формулою (2.12):
9 |
|
9 |
xdx |
|
|
M ( X ) = ∫ xf (x)dx = 1 |
∫ |
. |
|||
|
|||||
1 |
6 |
1 |
3 (x − 1)2 |
||
Виконавши заміну x − 1 = t 3 , перейдемо до змінної інтегрування
2 |
(t3 |
+ 1)dt = 3. |
t (0; 2): M ( X ) = 12 ∫0 |
||
84 |
|
|
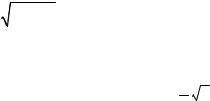
Дисперсію обчислюємо за формулою (2.18), знову застосовуючи при інтегруванні заміну змінної x − 1 = t3 :
D( X ) = |
1 9 |
x2dx |
− 9 = |
1 |
2 |
(t |
3 |
+ 1) |
2 |
dt − 9 |
≈ 5,143, |
σ ( X ) ≈ 2,268. |
6 1∫ |
|
2 |
∫0 |
|
|
|||||||
3 (x − 1)2 |
|
|
г) Імовірність того, що в результаті випробування Х набуде можливого значення з інтервалу (0; 1), знайдемо за формулою (2.5):
P{1 < X < 3}= F(3)− F(1) = 12 3 2 ≈ 0,63.
1.5.3. Початкові і центральні моменти випадкової величини та зв’язок між ними
Крім розглянутих характериcтик випадкової величини застосовуються й інші, які характеризують той чи інший бік розподілу випадкової величини. До них належать початкові і центральні моменти різних порядків.
Початковим моментом k-го порядку νk (X ) випадкової величини
X називається математичне сподівання k-го степеня цієї величини:
νk (X ) = M (X k ) .
Для дискретної випадкової величини, заданої рядом розподілу (2.1), початковий момент k-го порядку згідно з означенням математичного сподівання обчислюється за формулою:
n |
|
νk (X ) = ∑ xik pi . |
(2.19) |
i=1 |
|
Для неперервної випадкової величини X , |
що має щільність роз- |
поділу f (x) при x (−∞; ∞), початковий момент k-го порядку згідно з формулою (2.12) виражається інтегралом
|
∞ |
|
νk (X ) = |
∫ xk f (x)dx. |
(2.20) |
−∞
Розглянемо вирази для початкових моментів першого і другого порядків, що дасть змогу пов’язати початкові моменти з основними
85
числовими характеристиками випадкової величини — математичним сподіванням і дисперсією:
ν1 (X ) = M (X ), |
(2.21) |
|||
ν2 (X ) = M (X 2 ), |
||||
|
||||
отже, за формулою (2.17): |
|
|
|
|
D(X ) = ν |
2 |
(X ) − ν2 (X ) . |
(2.22) |
|
|
1 |
|
||
Центральним моментом k-го порядку μk (X ) |
випадкової вели- |
|||
чини X називається математичне сподівання k-го степеня її відхилення від математичного сподівання:
μk (X ) = M{[X − M (X )]k } .
Для дискретної випадкової величини з рядом розподілу (2.1)
n
μk (X ) = ∑[xi − M (X )]k pi , (2.23)
i=1
для неперервної випадкової величини зі щільністю розподілу f (x) при x (−∞;∞)
∞ |
|
μk (X ) = ∫ [x − M (X )]k f (x)dx. |
(2.24) |
−∞
Зауважимо, що відхилення X − M (X ) — також випадкова величина, але приведена до центру (середнього значення) можливих значень випадкової величини X . Тому величину X = X − M (X ) нази-
вають ще центрованою випадковою величиною, звідки походить назва центральних моментів.
Розглянемо центральні моменти 1-го, 2-го, 3-го і 4-го порядків, найчастіше застосовувані на практиці, і встановимо їхній зв’язок із початковими моментами.
За властивістю 5 математичного сподівання:
μ1 (X ) = M[X − M (X )] = 0 , |
(2.25) |
а за означенням дисперсії: |
|
μ2 (X ) = M{[X − M (X )]2} = D(X ) , |
(2.26) |
86
звідки за формулою (2.17)
μ2 (X ) = ν2 (X ) − ν12 (X ) .
Розкриваючи степінь [X − M (X )]3 , дістаємо вираз центрального момента 3-го порядку через початкові моменти:
μ3 (X ) = M{[X − M (X )]3} = |
|
|||||
= ν |
(X ) − 3ν |
2 |
(X )ν (X ) + 2ν3 |
(X ). |
(2.27) |
|
3 |
|
1 |
1 |
|
|
|
Аналогічно, розкривши степінь [X − M (X )]4 , дістанемо вираз центрального момента 4-го порядку через початкові моменти:
μ4 (X ) = ν4 ( X ) − 4ν3 (X )ν1 (X ) + 6ν2 (X )ν12 (X ) − 3ν14 (X ) . (2.28)
Приклад 2.12. Знайти початкові і центральні моменти 1-го, 2-го, 3-го і 4-го порядків дискретної випадкової величини X — кількості надійних приладів у системі, ряд розподілу якої побудовано у прикладі 2.1.
Розв’язання. Математичні сподівання випадкової величини X та її квадрата обчислено у прикладі 2.8: M (X ) = 2,4 , M (X 2 ) = 6,22 .
Отже, за формулами (2.21)
ν1 (X ) = 2, 4; ν2 (X ) = 6,22.
Далі за означенням початкових моментів:
ν3 (X ) = M (X 3 ) = 0,092 + 8 0,398 + 27 0,504 = 16,884;
ν4 (X ) = M (X 4 ) = 0,092 + 16 0,398 + 81 0,504 = 47,284.
Отже, початкові моменти до 4-го порядку заданої випадкової величини мають значення:
ν1 (X ) = 2,4; ν2 (X ) = 6,22; ν3 (X ) = 16,884; ν4 (X ) = 47,284.
Обчислимо центральні моменти, використовуючи формули (2.25)— (2.28).
Дисперсію знайдено в прикладі 2.8: D(X ) = 0,46 , тому:
μ1 (X ) = 0; μ2 (X ) = 0,46;
μ3 (X ) = 16,884 − 3 6,22 2,4 + 2 (2,4)3 = −0,252;
μ4 (X ) = 47,284 − 4 16,884 2,4 + 6 6,22 (2,4)2 − 3 (2,4)4 = 0,628.
87

Таким чином,
μ1 (X ) = 0; μ2 (X ) = 0,46; μ3 (X ) = −0,252; μ4 (X ) = 0,628.
Приклад 2.13. Неперервна випадкова величина X , розглянута в прикладі 2.9, має щільність розподілу
ln x |
ï ðè |
x (1; e); |
f (x) = {0 |
ï ðè |
x (1; e). |
Знайти початкові і центральні моменти 1-го, 2-го, 3-го і 4-го порядків цієї величини.
Розв’язання. За формулою (2.12) та формулою для інтеграла
e |
nen+1 +1 |
|
||
∫ xn ln xdx = |
|
|
|
, |
(n +1) |
2 |
|
||
1 |
|
|
|
|
яку легко дістати інтегруванням частинами, маємо такі значення початкових моментів:
ν (X ) = e2 + 1 |
≈ 2,1; |
ν |
2 |
(X ) = 2e3 + 1 |
≈ 4,57; |
||||
|
1 |
4 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
||
ν3 |
(X ) = 3e4 + 1 |
≈ 10,3; |
ν4 |
(X ) = 4e5 + 1 |
≈ 23,79. |
||||
|
|
16 |
|
|
|
|
25 |
|
|
Центральні моменти обчислюються за формулами (2.25)—(2.28). Дисперсію D(X ) знайдено у прикладі 2.9: D(X ) = 0,46 , тому
μ1 (X ) = 0; μ2 (X ) = 0,46;
μ3 (X ) = 10,3 − 3 4,57 2,1+ 2 (2,1)3 = 0,031;
μ4 (X ) = 23,79 − 4 10,3 2,1+ 6 4,57 (2,1)2 − 3 (2,1)4 = −0,152.
Зауваження. Якщо випадкова величина X має розподіл, симетричний відносно моди Mo(X ), то всі центральні моменти
непарних порядків дорівнюють нулю, оскільки при непарному k для дискретної випадкової величини у формулі (2.23) кожному додатному члену відповідає такий, що дорівнює йому за абсолютною величиною, від’ємний, а для неперервної випадкової величини у формулі (2.24) обчислюється інтеграл у симетричних межах від непарної функції.
88

|
|
Т.1 |
ВПРАВИ ДЛЯ АУДИТОРНОЇ |
||||||
|
|
ТА САМОСТІЙНОЇ РОБОТИ |
|
|
|||||
1. Дискретна випадкова величина Х має ряд розподілу: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Х |
– 1 |
|
0 |
1 |
|
2 |
|
|
|
Р |
0,1 |
|
2а |
0,2 |
|
5а |
|
|
1) Знайти ймовірності |
p2 і p4 можливих значень Х = 0 і Х= 2 ви- |
||||||||
падкової величини; 2) знайти вираз функції розподілу F (x) та по-
будувати її графік; 3) обчислити ймовірності попадання Х у проміж-
ки: а) [–1; 1]; б) (–1; 0,5).
2. Дискретна випадкова величина Х має функцію розподілу:
0, |
x ≤ −3, |
0,6, |
−3 < x ≤ 1, |
|
1 < x ≤ 2, |
F (x) = 0,8, |
|
|
2 < x ≤ 2,5, |
0,9, |
|
1, |
x > 2,5. |
Побудувати ряд розподілу величини Х і обчислити ймовірності випадкових подій: а) X > 1; б) X ≤ 2; в) 0 ≤ X ≤ 2,5.
3.Для випадкової величини Х, заданої рядом розподілу в задачі 1, знайти математичне сподівання, дисперсію, середнє квадратичне відхилення і моду.
4.Для випадкової величини Х, заданої функцією розподілу в задачі 2, знайти математичне сподівання, дисперсію, середнє квадратичне відхилення і моду.
5.Дискретну випадкову величину Х задано рядом розподілу:
Х |
– 0,1 |
0,2 |
0,4 |
Р |
p1 |
p2 |
p3 |
Знайти p1, p2 , p3, якщо відомі математичне сподівання M ( X ) = 0,21 і дисперсія D( X ) = 0,0469, побудувати функцію розподілу F (x) та
обчислити ймовірність того, що величина Х у результаті випробування набуде можливого значення з проміжку [0; 0,2].
89

6. Дискретну випадкову величину Х задано рядом розподілу:
|
Х |
– 2 |
|
x2 |
|
x3 |
|
|
4 |
|
|
|
Р |
p1 |
|
0,3 |
|
0,2 |
|
0,1 |
|
||
|
|
|
|
|
|||||||
Знайти x2 , x3 , p1 , якщо x2 < x3 |
і відомі математичне сподівання |
||||||||||
M (X )= −0,7 та дисперсія |
D(X ) |
= 3,01 , |
побудувати функцію роз- |
||||||||
поділу F (x) , обчислити імовірність того, |
що величина Х у ре- |
||||||||||
зультаті випробування набуде можливого значення з проміжку
[–2; 0].
7.Авіакомпанія виконує щоденно 2 рейси. Імовірність затримки першого рейсу за метеоумовами дорівнює 0,05, другого — 0,1. Скласти ряд розподілу випадкової величини Х — кількості затриманих рейсів та знайти математичне сподівання, дисперсію, середнє квадратичне відхилення і моду цієї випадкової величини.
8.Три контролери оцінюють якість виробу. Імовірність приймання виробу першим контролером дорівнює 0,6, другим — 0,5, третім — 0,4. Скласти ряд розподілу випадкової величини Х — кількості контролерів, які прийняли виріб, знайти математичне сподівання, дисперсію, середнє квадратичне відхилення і моду цієї випадкової величини.
9.Неперервна випадкова величина Х має щільність імовірності:
0,
f (x)= A2 x −0,
x3 , 4
x ≤ 0,
0 < x ≤ 2,
x > 2.
Знайти параметр А, математичне сподівання, дисперсію, середнє квадратичне відхилення, моду і медіану цієї випадкової величини.
10. Неперервна випадкова величина Х має щільність імовірності:
0, |
x ≤ 2, |
f (x)= A |
(− x2 + 6x − 8), 2 < x ≤ 4, |
|
x > 4. |
0, |
Знайти параметр А, математичне сподівання, дисперсію, середнє квадратичне відхилення, моду і медіану цієї випадкової величини.
90
