Теорія ймовірності - high_math

Тема 3. ДВОВИМІРНИЙ РОЗПОДІЛ.

СТАТИСТИЧНІ ГІПОТЕЗИ. ЕЛЕМЕНТИ КОРЕЛЯЦІЙНОГО ТА РЕГРЕСІЙНОГО АНАЛІЗУ

Вибірка, двовимірний статистичний розподіл, парний статистичний розподіл. Статистичні оцінки параметрів системи. Перевірка гіпотези про незалежність системи двох випадкових величин. Перевірка гіпотези про однорідність вибірок. Рівняння лінійної регресії. Нелінійна регресія. Метод найменших квадратів.

Література: [3, розділ 1, § 1.3]; [8, розділ 4, тема 12, п. 4, 5]; [9, розділ 3, § 3, 5]

Т.3 ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ТА ТИПОВІ ПРИКЛАДИ

3.1. Вибірка. Статистичний розподіл вибірки

Нехай над системою випадкових величин ( X , Y ) в однакових умовах проведено n незалежних випробувань. Вибіркою обсягом n

221

є послідовність ( x1, y1 ); ( x2 , y2 ); … ( xn , yn ) пар значень, яких набу-

вають складові X та Y системи в цих випробуваннях. Попереднє уявлення про залежність між X та Y можна дістати, якщо нанести

елементи вибірки ( xi , yi ), i = 1, 2, 3 ... n у вигляді точок на площині

у вибраній системі координат. Таке подання вибірки системи двох випадкових величин називається діаграмою розсіювання.

Якщо у вибірці обсягом n елемент xj спостерігається nj раз, а елемент yi – ni раз, то послідовність пар {(xj ,nj ); ( yi , ni )} називають

статистичним рядом. При цьому ∑ ni = n i ∑ nj = n .

i j

Перелік варіант Y = yi , X = xj та відповідних їм частот nij спільної

їх появиутворюють двовимірнийстатистичнийрозподіл вибірки.

У табличній формі цей розподіл має такий вигляд:

їм частот при фіксованому значенні X .

Y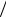 X = xj

222

k

Тут ∑ nij = nx j .

i=1

m

Тут ∑ nij = nyi .

j=1

Якщо частота спільної появи ознак X і Y nij = 1 для всіх варі-

ант, то в цьому разі двовимірний статистичний розподіл набирає такого вигляду:

Його називають парним статистичним розподілом вибірки.

Для системи двох та більшої кількості випадкових величин, як і для однієї випадкової величини, розглядають таке поняття, як інтервальний статистичний ряд розподілу, будують полігон і гістограму частот (для кожної випадкової величини, що входить у систему).

3.2. Статистичні оцінки параметрів системи

Система випадкових величин (X,Y) характеризується такими параметрами: математичними сподіваннями M(X) i M(Y) випадкових величин, що визначають положення центра розподілу (M(X), M(Y)); дисперсіями D(X) i D(Y), що визначають розсіювання розподілу від-

носно центра; кореляційним моментом K XY , який крім розсіювання випадкових величин X та Y може характеризувати взаємозв’язок цих

223

Якщо для системи випадкових величин побудовано інтервальний статистичний розподіл, точкові оцінки невідомих математичних сподівань, дисперсії, кореляційного момента також знаходять за фо-

рмулами (3.12) — (3.18), в які замість xi та yi підставляються середини (центри) xi* та yi* відповідних інтервалів.

Приклад 3.13. За даним двовимірним статистичним розподілом вибірки ознак X i Y

знайти статистичні оцінки параметрів.

+(4 − 5,8) 10 + (6 − 5,8) 5 + (8 − 5,8) 15) + (20 − 24)((2 − 5,8) 2 +

+(4 − 5,8) 8 + (6 − 5,8) 10 + (8 − 5,8) 0) + (30 − 24)((2 − 5,8) 4 +

+(4 − 5,8) 6 + (6 − 5,8) 5 + (8 − 5,8) 15) + (40 − 24)((2 − 5,8) 4 +

+(4 − 5,8) 6 + (6 − 5,8) 0 + (8 − 5,8) 10)] = 991 [(−14) (−18 + 1+ 33) − − 4 (−7,6 − 14, 4 + 2) + 6 (−15, 2 − 10,8 + 1+ 33) + 16 (−15,2 −

−10,8 + 22)] = 991 (−224 + 80 + 48 − 64) ≈ −1,62.

Оскільки KXY = −1,62, то це свідчить про те, що між ознаками X

i Y існує від’ємний кореляційний зв’язок.

Для вимірювання тісноти цього зв’язку обчислимо вибірковий

Тіснота кореляційного зв’язку між ознаками X i Y є слабкою.

226

3.3. Перевірка гіпотези про незалежність системи двох випадкових величин

Гіпотезу про незалежність двох випадкових величин Х та Y можна перевірити за критерієм χ2 . У цьому випадку величина χ2 визначається формулою

де nij — кількість випадків, коли одночасно спостерігались значення

ni0 , n0 j — загальна кількість випадків, коли спостерігались відповідно значення X = xi , Y = y j , l та m — кількість значень, що їх на-

бувають відповідно величини X та Y за умови, що обсяг вибірки дорівнює n.

Гіпотеза H0 про незалежність випадкових величин X та Y приймається на рівні значущості α, якщо χ2 ≤ χα2 , де значення χα2 береться з таблиць розподілу χ2 з k = (n − 1)(m − 1) ступенями свободи (дод. 3). Інакше кажучи, гіпотеза Н0 відхіляється на рівні значущості

α, якщо χ2 ≥ χ2−α .

1

Для обчислення вибіркового значення статистики (3.19) критерію

Результати перевірки гіпотези можна подати у вигляді таблиці спряженості ознак l × m (табл. 3.11), яка являє собою сукупний результат послідовності повторень випадкового експерименту (прицьому результати класифікуються за двома змінними ознаками).

Нехай є k різних експериментів, що складаються з n1, n2 , ..., nk одиничних спостережень, тобто k різних вибірок обсягу n1,

n2 , ..., nk .

Потрібно перевірити гіпотезу про те, що k вибірок вибрано з однієї і тієї самої сукупності або, інакше кажучи, гіпотезу про те, що ці вибірки однорідні.

227

У кожному екперименті спостерігається деяка змінна ознака і результати кожного зі спостережень розбиваються за значеннями цієї

ознаки на l груп. Кількість результатів спостережень в i-й групі j-го ряду позначимо nij . Тоді всі дані розміщуються в таблиці такого са-

мого вигляду, як і таблиця 3.11, причому суми за стовпцями в ній дорівнюють n j .

Проте в цьому випадку таблиця є результатом спостережень не однієї послідовності, як у випадку табл. 3.11, а k незалежних спостережень, кожному з яких відповідає один стовпець. Для перевірки гіпотези про однорідність використовують той самий критерій, що й для перевірки незалежності двох ознак.

Приклад 3.14. У 20 рейсах при різних погодних умовах здійснювались вимірювання максимальної швидкості і висоти польоту. Відхилення від розрахункових (у м/с і відповідно в м) наведено в табл. 3.12.

Таблиця 3.12

Закінчення табл. 3.12

228

а) Скласти інтервальний статистичний ряд розподілу системи (X, Y); б) знайти точкові оцінки математичного сподівання, дисперсії,

кореляційного момента та коефіцієнта кореляції; в) перевірити гіпотезу про незалежність цих випадкових величин

на рівні значущості α = 0,05.

Розв’язання.

а) Випишемо різні значення варіант, які потрапили у вибірку, у порядку їх зростання. Дістанемо дискретний варіаційний ряд:

Визначаємо за обсягом вибірки n = 20 орієнтовну кількість m = 5 частинних інтервалів в інтервальному статистичному розподілі. За формулами

hx = (xmax − xmin ) / m та hy = ( ymax − ymin ) / m

обчислюємо крок інтервалів

hx = (20 + 16) / 5 = 7,2; hy = (62 + 32) / 5 = 18,8.

Підсумуємо частоти варіант, які потрапили в кожний із частинних інтервалів, при цьому частоти варіант, які збіглися з межами інтервалів, поділимо порівну між суміжними інтервалами.

Тоді інтервальний статистичний розподіл вибірки можна подати у вигляді табл. 3.13.

yB = 201 (−32 − 30 − 15 − 10 2 − 8 2 − 2 + 2 + 3 2 + 5 + 8 + +10 + 18 + 22 2 + 28 + 55 + 62) = 6,15,

sX2 = 191 ((−16 − 1, 2)2 + (−12 − 1,2)2 + (−11− 1, 2)2 +

+(−10 − 1,2)2 + (−8 − 1,2)2 + (−2 − 1, 2)2 2 + (−1− 1,2)2 2 +

+(1− 1,2)2 + (2 − 1,2)2 + (4 − 1,2)2 2 + (6 − 1, 2)2 2 +

+(8 − 1, 2)2 + (10 − 1, 2)2 + (12 − 1, 2)2 +

+(14 − 1, 2)2 + (20 − 1,2)2 ) = 88,38,

sY2 = 191 ((−32 − 6,15)2 + (−30 − 6,15)2 + (−15 − 6,15)2 +

+(−10 − 6,15)2 2 + (−8 − 6,15)2 2 + (−2 − 6,15)2 + (2 − 6,15)2 +

+(3 − 6,15)2 2 + (5 − 6,15)2 + (8 − 6,15)2 + (10 − 6,15)2 +

+(18 − 6,15)2 + (22 − 6,15)2 2 + (28 − 6,15)2 + (55 − 6,15)2 +

+(62 − 6,15)2 ) = 572,66.

KXY = 191 [(−10 − 1,2)(−8 − 6,15) + (−2 − 1, 2)(−10 − 6,15) +

+(4 − 1,2)(22 − 6,15) + (10 − 1,2)(55 − 6,15) +

+(−1− 1, 2)(2 − 6,15) + (−16 − 1,2)(−30 − 6,15) +

+(−8 − 1,2)(−15 − 6,15) + (−2 − 1,2)(5 − 6,15) +

+(6 − 1,2)(10 − 6,15) + (8 − 1,2)(18 − 6,15) +

+(−1− 1,2)(3 − 6,15) + (4 − 1, 2)(−2 − 6,15) +

+(12 − 1, 2)(28 − 6,15) + (20 − 1, 2)(62 − 6,15) +

+(−11− 1,2)(−10 − 6,15) + (2 − 1,2)(−8 − 6,15) +

+(14 − 1, 2)(22 − 6,15) + (6 − 1,2)(3 − 6,15) +

+(−12 − 1, 2)(−32 − 6,15) + (1− 1, 2)(8 − 6,15)] = 197,86.

Для обчислення коефіцієнта кореляції застосуємо формулу

230