
Теорія ймовірності - high_math
.pdf
|
0, |
|
|
|
x ≤ −1, |
|
|||||
1.2.13. F (x)= |
A |
|
x + 1, |
−1 < x ≤ 3, |
|||||||
|
|
1, |
|
|
|
x > 3. |
|
||||
|
|
|
|
|
|
||||||
|
0, |
(− x2 + 4x) |
|
|
|
|
x ≤ 0, |
||||
1.2.14. F (x)= |
A |
, |
|
|
|
0 < x ≤ 2, |
|||||
|
|
1, |
|
|
|
|
|
|
|
x > 2. |
|
|
|
|
|
|
|
|
|
|
|||
|
0, |
|
|
|
|
|
|
|
|
x ≤ −2, |
|
|
|
|
|
π |
|
x |
|
|
|||
1.2.15. |
F (x)= |
A |
|
4 |
+ arctg |
|
|
|
, |
−2 < x ≤ 2, |
|
|
|
||||||||||
|
|
|
|
|
2 |
|
x > 2. |
||||
|
1, |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
x ≤ −2, |
|
|
|
|
|
π |
|
|
x |
|
|
||
1.2.16. |
F (x)= |
A |
|
|
+ arcsin |
|
|
|
, |
−2 < x ≤ 2, |
|
2 |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
x > 2. |
|||
|
1, |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
x ≤ − π 2, |
||
1.2.17. F (x)= |
A(sin x + 1), |
|
|
|
|
− π 2 < x ≤ π 2, |
|||||
|
|
1, |
|
|
|
|
|
|
|
x > π 2. |
|
|
|
|
|
|
|
|
|
|
|||
|
0, |
|
|
|
|
|
|
|
x ≤ 0, |
||
1.2.18. F (x)= |
A(1− cos x), |
|
|
|
|
0 < x ≤ π , |
|||||
|
|
1, |
|
|
|
|
|
|
|
x > π. |
|
|
|
|
|
|
|
|
|
|
|||
|
0, |
|
|
|
|
|
|
x ≤ −1, |
|||
1.2.19. |
f (x) = |
Aln (2 + x), |
|
|
|
|
−1 < x ≤ 1, |
||||
|
|
0, |
|
|
|
|
|
|
x > 1. |
||
|
|
|
|
|
|
|
|
||||
|
0, |
|
|
x ≤ 3π / 4, |
|||||||
1.2.20. |
f (x) = |
Asin 2x, 3π / 4 < x ≤ π, |
|||||||||
|
|
0, |
|
|
x > π. |
|
|||||
|
|
|
|
|
|||||||
|
0, |
|
|
|
|
|
|
|
|
x ≤ 0, |
|
1.2.21. F (x)= |
A(x + 0,5sin 2x), |
0 < x ≤ π / 2, |
|||||||||
|
|
1, |
|
|
|
|
|
|
|
|
x > π / 2. |
|
|
|
|
|
|
|
|
|
|
||
(0; 2).
(0; 1).
(0; 233 ).
(–1; 1).
(− π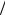 3; π
3; π 3).
3).
(0; π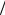 2).
2).
(0; 2).
(5π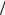 6; π).
6; π).
(π 6; π
6; π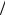 3).
3).
101
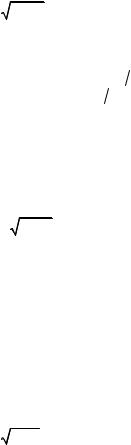
0, |
x ≤ −1, |
|
1.2.22. F (x)= |
A(2arcsin x + π), |
−1 < x ≤ 1, |
|
1, |
x > 1. |
|
||
|
0, |
|
|
|
|
|
|
||
1.2.23. |
f (x) = |
|
|
A |
|
, |
|
|
|
|
|
|
2 |
||||||
|
|
1+ x |
|
|
|
|
|||
|
|
0, |
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
1.2.24. |
f (x) = |
|
|
|
|
|
, |
||
|
|
|
|
|
|
|
|||
|
|
|
1+ x2 |
||||||
|
0, |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
||
1.2.25. |
f (x) = |
|
Acos2 x, |
||||||
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0, |
|
|
|
|
|
|
|
1.2.26. |
f (x) = |
|
Ax |
, |
|
||||
|
2 |
||||||||
|
|
1+ x |
|
|
|
|
|||
|
|
0, |
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
||
1.2.27. |
f (x) = |
|
A 1− x2 , |
||||||
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0, |
|
|
|
|
|
|
|
1.2.28. |
f (x) = |
|
Asin2 x, |
||||||
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.2.29. |
f (x) = |
0, |
|
− x |
, |
|
|
||
|
Axe |
|
|
|
|
||||
|
|
0, |
|
|
|
|
|
|
|
1.2.30. |
f (x) = |
A |
|
|
, |
||||
|
|
x + |
3 |
||||||
|
|
|
|
|
|
||||
|
0, |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
x ≤ 0,
0 < x ≤ 1, x > 1.
x ≤ −1, −1 < x ≤ 1,
x> 1.
x≤ 0,
0 < x ≤ π 2, x > π 2.
x ≤ 0,
0 < x ≤ 3, x > 3.
x ≤ 0,
0 < x ≤ 1,
x> 1.
x≤ 0,
0 < x ≤ π, x > π.
x ≤ 0,
0 < x < ∞.
x ≤ −3, −3 < x ≤ 1,
x > 1.
(0; 0,5).
(0; 2).
(0; 1).
(− π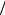 4; π
4; π 4).
4).
(0; 1).
(–1/2; 1/2).
(− π 4; π
4; π 2) .
2) .
(0; 1).
(–1; 1).
102

Тема 2. ОСНОВНІ РОЗПОДІЛИ ДИСКРЕТНИХ
ВИПАДКОВИХ ВЕЛИЧИН
Імовірнісна твірна функція. Біноміальний розподіл дискретної випадкової величини. Розподіл Пуассона. Геометричний розподіл. Гіпергеометричний розподіл. Числові характеристики дискретних випадкових величин, розподілених за основними законами.
Література: [1, глава5, п. 5.9], [2, глава5], [4, глава6, § 4—5], [7, тема 9].
Т.2 ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ТА ТИПОВІ ПРИКЛАДИ
2.1. Імовірнісна твірна функція та її застосування для знаходження числових характеристик дискретних розподілів
Нехай дискретна випадкова величина X набуває можливих зна-
чень k з імовірностями pk |
(k = 0, 1, 2, ..., n, ...) . |
|
Твірною функцією ϕ(z) |
для такої випадкової величини назива- |
|
ється функція |
|
|
|
∞ |
|
|
ϕ(z) = ∑ pk zk , |
(2.29) |
|
k =0 |
|
де z — довільний параметр (0 < z < 1) .
Якщо випадкова величина має скінченну множину можливих значень n, то твірна функція набирає вигляду
n
ϕ(z) = ∑ pk zk .
k =0
Через значення похідних твірної функції при z = 1 виражаються основні числові характеристики дискретної випадкової величини з розглядуваним розподілом.
Зокрема, перша похідна твірної функції
∞
ϕ′(z) = ∑ kpk zk −1
k =0
103
при z = 1 дорівнює математичному сподіванню величини X :
∞
ϕ′(1) = ∑ kpk = M (X ) = ν1 (X ). (2.30)
k =0
Друга похідна твірної функції
∞
ϕ′′(z) = ∑ k(k − 1) pk zk −2
k =0
при z = 1 виражається через початкові моменти першого і другого порядків:
∞ |
∞ |
∞ |
(X ) − ν1 (X ). |
ϕ′′(1) = ∑ k(k − 1) pk = ∑ k2 pk − ∑ kpk = ν2 |
|||
k =0 |
k =0 |
k =0 |
|
Шляхом нескладних перетворень у формулі (2.22) через значення похідних твірної функції при z = 1 виражається дисперсія випадкової величини:
D(X ) = ν2 (X ) − ν12 (X ) = ν2 (X ) − ν1 (X ) + ν1 (X ) − ν12 ( X ) = (2.31) = ϕ′′(1) + ϕ′(1) − [ϕ′(1)]2 .
Формули (2.30) і (2.31) застосовуються для знаходження основних числових характеристик дискретних випадкових величин з найбільш поширеними законами розподілу.
2.2. Розподіли цілочисельної дискретної випадкової величини
2.2.1. Біноміальний розподіл
Біноміальний закон розподілу виникає у схемі Бернуллі, коли проводиться n незалежних випробувань, у кожному з яких випад-
кова подія A може або відбутися зі сталою ймовірністю |
p, або не |
||||
відбутися з імовірністю |
q = 1 − p , а випадкова величина |
X — кіль- |
|||
кість появ події A в цих n випробуваннях. |
|
||||
Дискретна величина |
|
X |
набуває цілих невід’ємних значень k |
||
(k = 0, 1, 2, ..., n) з імовірностями |
pk , які обчислюються за форму- |
||||
лою Бернуллі (1.23): |
|
|
|
|
|
p |
k |
= P (k) = C k pk qn−k , |
|
||
|
|
n |
n |
|
|
104

тобто величина X має ряд розподілу
X |
0 |
1 |
2 |
... |
k |
... |
n |
|
|
|
|
|
|
|
|
P |
qn |
Cn1 pqn−1 |
Cn2 p2qn− 2 |
... |
Cnk pk qn− k |
... |
pn |
|
|
|
|
|
|
|
|
Імовірності pk дорівнюють відповідним членам розкладу |
n -го |
||||
степеня бінома |
|
|
|
|
|
(q + p)n = qn + Cn1qn−1 p + Cn2qn− 2 p2 + ... + |
|
(2.32) |
|||
|
n |
|
|
|
|
+ Cnk qn− k pk + ... + pn = ∑ Cnk qn−k pk , |
|
|
|||
|
k =0 |
|
|
|
|
звідки походить назва цього розподілу. |
|
|
M (X ), |
D(X ), |
σ(X ) |
Для знаходження основних характеристик |
|||||
біноміального розподілу використовується твірна функція |
|
||||
n |
|
|
|
|
|
ϕ(z) = ∑ Cnk pk qn−k zk , |
|
|
|
||
k =0 |
|
|
|
|
|
яка згідно з формулою (2.32) набирає вигляду: |
|
|
|
||
ϕ(z) = (q + pz)n . |
|
|
|
|
|
′ |
+ pz) |
n−1 |
p при |
z = 1 набуває |
|
Її перша похідна за z ϕ (z) = n(q |
|
||||
значення |
|
|
|
|
|
ϕ′(1) = n(q + p)n−1 p = np , |
|
|
|||
яке, згідно з формулою (2.30), дорівнює М(Х), тобто |
|
|
|||
М(Х) = np. |
|
|
|
(2.33) |
|
Друга похідна твірної функції ϕ′′(z) = n(n − 1)(q + pz)n−2 p2 при z = 1 набуває значення
ϕ′′(1) = n(n − 1)(q + p)n− 2 p2 = n(n − 1) p2 ,
тому за формулою (2.31) маємо дисперсію
D(X ) = n(n − 1) p2 + np − n2 p2 = np(1− p) = npq |
(2.34) |
і, відповідно, середнє квадратичне відхилення
σ(X ) = npq.
105
Приклад 2.14. За метеорологічних умов, що склалися в аеропорту, імовірність своєчасного відправлення кожного рейсу дорівнює 0,6. Випадкова величина X — кількість своєчасно відправлених рейсів з трьох передбачених розкладом. Скласти ряд розподілу і
знайти M (X ) і σ ( X ) цієї випадкової величини.
Розв’язання. Випадкова величина X набуває можливих значень 0,1, 2, 3 , а відповідні ймовірності обчислюються за формулою Бер-
нуллі при n = 3; p = 0,6; q = 0,4 :
p0 = P3 (0) = 0,43 = 0,064;
p1 = P3 (1) = C31 0,6 0,42 = 0,288; p2 = P3 (2) = C31 0,62 0,4 = 0,432; p3 = P3 (3) = 0,63 = 0,216.
Отже, випадкова величина має ряд розподілу
X |
0 |
1 |
2 |
3 |
P |
0,064 |
0,288 |
0,432 |
0,216 |
Математичне сподівання і дисперсію обчислено за формулами
(2.33) і (2.34):
M (X ) = np = 1,8; D( X ) = npq = 0,72; σ(X ) ≈ 0,85.
2.2.2. Розподіл Пуассона
Розподіл Пуассона виникає в схемі Бернуллі, коли кількість n виконуваних незалежних випробувань велика, імовірність p появи
події A в кожному випробуванні мала, а випадкова величина X — кількість появ події A в цих n випробуваннях.
У цьому випадку масових |
рідкісних подій випадкова величина |
X набуває цілих невід’ємних |
значень k (k = 0, 1, 2, ..., n) з імовір- |
ностями pk , які обчислюються за формулою Пуассона (1.29):
p |
= P (k) ≈ λk |
e− λ |
(λ = np) , |
|
k |
n |
k! |
|
|
|
|
|
|
|
106
тобто величина X має ряд розподілу
X |
0 |
1 |
|
2 |
... |
|
k |
... |
|
n |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
e− λ |
λe− λ |
λ2 |
|
e− λ |
... |
λk |
|
e− λ |
... |
λn |
|
e− λ |
|
|
|
2! |
|
|
k! |
|
|
n! |
|
|||
Для знаходження основних числових характеристик M (X ), D( X ) і σ ( X ) розподілу Пуассона застосовують твірну функцію
ϕ(z) = ∑ |
λ |
e |
|
zk = e− λ ∑ |
(λz) |
. |
n |
k |
|
− λ |
n |
|
k |
k =0 |
k! |
k =0 |
k! |
|
||
Оскільки n велике, то, використовуючи відомий розклад функції ex у степеневий ряд
|
x |
∞ |
xk |
|
e |
|
= ∑ |
|
, |
|
k! |
|||
|
|
k =0 |
|
можна подати твірну функцію у вигляді:
ϕ(z) = e− λ eλz = eλ ( z−1) .
Її перша похідна ϕ′(z) = λeλ ( z−1) , тому за формулою (2.30):
M (X ) = ϕ′(1) = λ .
Друга похідна твірної функції
ϕ′′(z) = λ2eλ ( z−1) ,
тому за формулою (2.31) дисперсія набуває значення:
D(X ) = ϕ′′(1) + ϕ′(1) − [ϕ′(1)]2 = λ2 + λ − λ2 = λ
і, відповідно, середнє квадратичне відхилення
σ(X ) = λ .
Отже, характерною особливістю розподілу Пуассона є те, що його математичне сподівання збігається з дисперсією. Це робить його простим, але й більш обмеженим за можливостями.
107
Приклад 2.15. Система бронювання та продажу авіаційних квитків має 1000 периферійних пультів. Імовірність надходження запиту з кожного пульта протягом однієї хвилини дорівнює 0,002. Знайти: а) закон розподілу випадкової величини X — кількості запитів, що надійдуть до системи протягом однієї хвилини; б) середню кількість запитів; в) імовірність надходження протягом однієї хвилини принаймні двох запитів.
Розв’язання. а) |
За умовою n = 1000, |
p = 0,002, |
тому λ = 2, от- |
||||||||||||||||||
же, ряд розподілу має вигляд |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
0 |
|
|
1 |
|
|
2 |
|
3 |
|
|
... |
|
1000 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
P |
|
1 |
|
|
|
2 |
|
|
|
22 |
|
|
23 |
|
|
... |
|
21000 |
|
|
|
|
e2 |
|
|
e2 |
|
|
2!e2 |
|
3!e2 |
|
|
1000!e2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
X |
0 |
|
|
1 |
|
|
2 |
|
3 |
|
|
... |
|
1000 |
|
|
||||
|
P |
0,135 |
|
0,271 |
|
0,271 |
0,180 |
|
... |
|
0,000 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Середня кількість (математичне сподівання) запитів, що надійде до системи протягом однієї хвилини, M (X ) = 2 .
в) Імовірність надходження протягом однієї хвилини принаймні двох запитів
P{2 ≤ X ≤ 1000} = 1− P(0) − P(1) = 0,594.
2.2.3. Геометричний розподіл
Геометричний розподіл виникає, коли незалежні випробування, у кожному з яких подія A може відбутися зі сталою ймовірністю p ,
проводяться до першого «невдалого» випробування (подія A не відбулась) і далі припиняються, а випадкова величина X — кількість проведених «вдалих» випробувань.
Дискретна величина X набуває цілих невід’ємних значень k
(k = 0, 1, |
2, ...) з імовірностями pk = pk q , оскільки X набуває зна- |
чень k , |
якщо в k випробуваннях подія A відбулась (імовірність |
pk ), а в наступному — не відбулась (імовірність q ).
108

Отже, X має такий нескінченний ряд розподілу:
X |
0 |
1 |
2 |
... |
k |
... |
|
|
|
|
|
|
|
P |
q |
pq |
p2q |
... |
pk q |
... |
|
|
|
|
|
|
|
Для знаходження числових характеристик M (X ), D(X ), σ ( X ) |
|
застосовують твірну функцію |
|
∞ |
∞ |
ϕ(z) = ∑ pk qzk = q ∑ ( pz)k , |
|
k =0 |
k =0 |
доданки якої 1, pz, ( pz)2 , ... є членами нескінченної спадної геометричної прогресії з першим членом u1 = 1 і знаменником b = pz < 1. Сума членів такої геометричної прогресії обчислюється за формулою
S = |
u1 |
= |
1 |
|
, тому ϕ(z) = |
q |
||||
|
|
|
|
|
. |
|||||
1 − b |
|
1 − pz |
|
1− pz |
||||||
Перша похідна твірної функції |
|
|
|
|||||||
|
|
|
ϕ′(z) = |
|
pq |
, |
|
|
||
|
|
|
|
(1− pz)2 |
|
|
||||
тому за формулою (2.30) математичне сподівання набуває значення:
|
M (X ) = ϕ′(1) = |
|
|
|
pq |
|
|
= |
|
p |
. |
|
|
|
|
(2.35) |
|||||||||||
|
(1 |
− p)2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|||||||||
Друга похідна твірної функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ϕ′′(z) = |
|
|
|
2 p2q |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
(1− pz)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
тому за формулою (2.31) дисперсія набуває значення: |
|
|
|
||||||||||||||||||||||||
D(X ) = |
|
2 p2q |
+ |
p |
|
− |
p2 |
|
= 2 |
p2 |
+ |
|
p |
|
− |
p2 |
= |
p |
(2.36) |
||||||||
|
(1− p)3 |
q |
q2 |
q2 |
|
|
q |
q2 |
q2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
і, відповідно, середнє квадратичне відхилення |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
σ(X ) = |
|
|
|
p |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.37) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
109

Зауваження. Практичне застосування має також розподіл випадкової величини X1 — кількості взагалі проведених випробувань. Ця величина набуває натуральних можливих значень
k (k = 1, 2, 3,...) |
з імовірностями |
p |
= pk −1q, |
тобто X |
1 |
має ряд |
|||||||
розподілу |
|
|
|
|
k |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 |
1 |
|
2 |
3 |
... |
|
k |
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
q |
|
pq |
p2q |
... |
|
pk −1q |
|
... |
|
|
|
Розподіл випадкової величини X1 є зміщеним на 1 відносно гео-
метричного розподілу, тому її основні числові характеристики обчислюються за формулами:
M (X1 ) = M (X + 1) = M (X ) + 1 = qp + 1 = 1q ;
D( X1 ) = D(X + 1) = D(X ) = qp2 ; σ(X1 ) = qp .
Знайдені формули мають місце у випадку нескінченного ряду розподілу. Проте в деяких задачах умови випробувань передбачають обмеження ряду розподілу, тобто геометрично розподілена випадкова величина X набуває можливих значень 0, 1, 2, ..., k . У цьому
випадку X набуває значень k , |
якщо в k-му випробуванні подія A |
|||||||||
не відбулась |
(імовірність |
pk q ) |
або відбулась |
(імовірність pk +1 ), |
||||||
тобто за теоремою додавання ймовірностей несумісних подій: |
||||||||||
|
|
P{X = k} = pk q + pk +1 = pk (q + p) = pk , |
||||||||
а ряд розподілу цієї випадкової величини набирає вигляду: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
0 |
1 |
2 |
|
... |
k − 1 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
q |
pq |
p2q |
|
... |
pk −1q |
|
pk |
|
Застосування формул (2.35)—(2.37) для знаходження основних числових характеристик цієї випадкової величини приводить до значних похибок, тому в цьому випадку доцільно використовувати загальні формули (2.11), (2.17).
110
