
Теорія ймовірності - high_math
.pdf
Сприятливими щодо події A є ті наслідки, в яких буде вибрано число, що закінчується нулем або п’ятіркою. Кількість таких наслідків m = 18 . Отже, за формулою (1.1) P(A) = 0,2.
Приклад 1.4. У групі із двадцяти студентів 30 % — відмінники. Для здачі заліку навмання викликано одного студента. Яка ймовірність того, що викликано відмінника?
Розв’язання. Позначимо подію В = {викликано відмінника}. Випробування полягає у випадковому виборі одного студента із двадцяти, тому загальна кількість наслідків n = 20. Оскільки за умовою в групі 6 відмінників, то кількість сприятливих щодо події А наслідків m = 6. За формулою (1.1) P(В) = 0,3.
Приклад 1.5. Із двоцифрових чисел, не більших від 20, навмання вибрано одне число q і складено рівняння x2 + 8x + q = 0. Яка ймо-
вірність того, що корені рівняння — дійсні цілі числа? Розв’язання. Випробування полягає у випадковому виборі одно-
го з одинадцяти чисел, тому n = 11. Позначимо подію С = {корені дійсні цілі числа}. Рівняння має дійсні корені, коли дискримінант
D = 16 – q ≥ 0 або q ≤ 16. Із формул для коренів рівняння x1, 2 =
= −4 ± 16 − q випливає, що лише 3 числа дають цілі значення коре-
нів. Отже, m = 3, а P(С) ≈ 0,272.
Приклад 1.6. Маємо 5 відрізків довжиною 1, 3, 6, 8 і 10 см. Яка ймовірність того, що з вибраних навмання трьох відрізків можна скласти трикутник?
Розв’язання. Позначимо подію В = {з вибраних відрізків можна скласти трикутник}. Загальна кількість наслідків випробування
n = C53 = 10. Події В сприяють тільки 3 наслідки: 3, 6, 8; 3, 8, 10; 6, 8, 10. Тому P(В) =0,3.
Приклад 1.7. Кожний із чотирьох пасажирів може придбати квиток на один із семи рейсів, що виконуються впродовж дня до аеропорту N. Знайти ймовірність того, що вони придбали квитки:
а) на перший рейс; б) на один і той самий рейс; в) на різні рейси.
Розв’язання. Оскільки для кожного пасажира є 7 варіантів придбання квитка, то, згідно з принципом добутку, кількість усіх на-
слідків випробування n = 74 .
11
а) Позначимо подію B = {всі пасажири придбали квитки на перший рейс}. Цій події сприяє лише один наслідок. Отже, mB = 1, а за
формулою (1.1) P(B) ≈ 0,0004 .
б) Позначимо подію C = {усі пасажири придбали квитки на один і той самий рейс}. Сприятливими щодо цієї події є 7 наслідків (за кількістю рейсів). Отже, mC = 7 , тому P(C) ≈ 0,0029 .
с) Позначимо подію D ={пасажири придбали квитки на різні рейси}. Кількість наслідків, сприятливих щодо цієї події, mD = A74 = 840 ,
тому P(D) ≈ 0,35 .
Приклад 1.8. У комплекті 9 виробів найвищої якості становлять 75 % усього комплекту. Випадковим чином відібрано 6 виробів. Знайти ймовірність того, що серед відібраних виробів:
а) усі найвищої якості; б) лише 4 найвищої якості.
Розв’язання. Оскільки 9 виробів становлять 75 %, то всього в комплекті міститься 12 виробів, три з яких не найвищої якості. Випробування полягає у виборі шести виробів із дванадцяти. Отже,
кількість усіх наслідків випробування n = C126 = 924 .
а) Позначимо подію A = {усі відібрані вироби найвищої якості}. Цій події сприяють лише ті наслідки, в яких відбір шести виробів
здійснюється з дев’яти найвищої якості. Отже, mA = C96 = C93 = 84 , а
P(A) ≈ 0,09 .
б) Позначимо подію B = {серед відібраних лише 4 вироби найвищої якості}. Сприятливими щодо цієї події є ті наслідки, в яких 4 вироби відбираються із дев’яти найвищої якості і 2 вироби із трьох
не найвищої якості. За принципом добутку mB = C94 C32 = 378 , а
P(B) ≈ 0,41.
Приклад 1.9. Вісім літаків, серед яких 2 Ан-140, що прибули в аеропорт, випадковим чином розміщені на стоянках, розташованих в одному ряду. Яка ймовірність того, що між літаками Ан-140 опиниться 1 літак іншого типу і не залишиться вільних стоянок, якщо кількість стоянок: а) дорівнює 10; б) дорівнює 8?
Розв’язання. а) Загальна кількість варіантів розміщення восьми літаків на десяти стоянках обчислюється за формулою (1.3):
n = A108 = 1 814 400.
12
Позначимо подію C ={між літаками Ан-140 є 1 літак іншого типу}. Кількість варіантів такого розташування для літаків Ан-140 з урахуванням варіантів, що виникають при заміні їх місцями, дорівнює 16. Для літака, який розташується між ними, є 6 варіантів, а для решти п’яти літаків кількість варіантів розташування на семи вільних стоян-
ках дорівнює A75 =2520.
За принципом добутку число mC наслідків, сприятливих щодо події C, дорівнює mC =16 · 6 · 2520 = 241 920, а ймовірність події C P(C) ≈ 0,133.
б) Загальна кількість варіантів розташування восьми літаків на восьми місцях обчислюється за формулою (1.4):
n = P8 = 8! = 40 320.
Кількість варіантів указаного в умові розміщення літаків Ан-140 дорівнює 12, а решти шести літаків на шести місцях, що залиши-
лись, P6 = 720. Отже, mC = 12 ·720 = 8640, а P(C) ≈ 0,214.
1.3. Геометричний підхід до обчислення ймовірностей
Класична формула (1.1) обчислення ймовірності події незастосовна, якщо простір Ω елементарних наслідків випробування є нескінченна множина. У цьому випадку застосовують геометричний підхід до знаходження ймовірностей, при якому проведення випробування інтерпретується як випадкове кидання точки в область Ω n-вимірного простору, а подія А — як потрапляння цієї точки в підобласть А області Ω. Множина всіх наслідків випробування виража-
ється відповідною мірою mΩ області Ω, а множина наслідків, спри-
ятливих щодо події A, — мірою mA області |
A. Імовірність події A |
||
обчислюється за формулою |
|
||
P( A) = |
mA |
. |
(1.5) |
|
|||
|
m |
|
|
|
Ω |
|
|
Зокрема, в одновимірному координатному просторі ймовірність у формулі (1.5) визначається відношенням довжин відрізків, у двовимірному просторі — відношенням площ плоских фігур, у тривимірному просторі — відношенням об’ємів просторових тіл. Отже, якщо довжину позначено через L , площу — через S і об’єм — через V , то формула (1.5) в одно-, дво-, тривимірному координатному просторі набирає відповідно такого вигляду:
13
P(A) = |
LA |
, P(A) = |
SA |
, P(A) = |
VA |
. |
(1.6) |
|
L |
|
|
||||||
|
|
S |
Ω |
V |
|
|||
|
Ω |
|
|
|
Ω |
|
||
Приклад 1.10. Відстань між пунктами А і В автобус долає за 3 хв, а пішохід — за 15 хв. Інтервал руху автобусів 30 хв. У випадковий момент часу із А до В вирушив пішохід. Знайти ймовірність того, що він прибуде в пункт В раніше від наступного автобуса.
Розв’язання. Позначимо через x час виходу пішохода з пункту А, тоді x набуває значень з інтервалу від 0 до 30 хв — інтервалу між відправленнями попереднього і наступного автобусів. Тому множина всіх
наслідків випробування відповідає довжині цього інтервалу: LΩ = 30.
Позначимо подію: А = {пішохід прибуде в В раніше від наступного автобуса}. Цій події сприяють наслідки, для яких 30 − x + 3 > > 15, де 30 — х — час до виходу на маршрут наступного автобуса, 3 хв — час руху автобуса, 15 хв — час руху пішохода. Звідси дістаємо x < 18. Отже, сприятливим щодо події А наслідкам відповідає
довжина інтервалу LA = 18. За першою з формул (1.6) P(A) = 0,6.
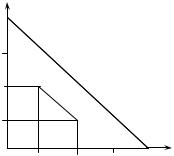
Приклад 1.11. На відрізку довжиною 12 см навмання поставлено дві точки. Яка ймовірність того, що довжина кожного з утворених при цьому послідовних відрізків буде не меншою від 3 см?
Розв’язання. Позначимо через x довжину першого відрізка, че- |
||
рез у — другого, тоді довжина третього відрізка |
становитиме |
|
12 − x − y. Множина всіх наслідків визначається умовами: |
x > 0; |
y > 0; |
x + y < 12. Множина |
точок, |
коор- |
|
y |
|
A |
|
|
|
динати яких задовольняють ці умо- |
|||||
12 |
|
|
|
|
ви, |
заповнює |
трикутник |
АОВ |
||||
|
|
|
|
|
|
|
|
(рис. 1.1) із площею 72 см2. Отже, |
||||
9 |
|
|
|
|
|
|
SΩ = 72. |
|
|
|
||
|
|
|
|
K |
|
|
|
Позначимо подію В = {довжи- |
||||
6 |
|
|
|
|
|
на |
кожного відрізка не менша за |
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
3 см}. Цій події сприяють наслідки, |
||||
3 |
|
|
L |
M |
|
|
для |
яких |
x ≥ 3; y ≥ 3; 12 − x − y ≥ 3 |
|||
|
|
|
|
|
В |
або |
x + y ≤ 9. |
Точки, координати |
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
12 x |
яких задовольняють ці умови, запо- |
||||
|
0 |
|
3 |
6 |
9 |
|||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
внюють трикутник KLM із площею |
||||
|
|
|
|
|
Рис. 1.1 |
|
|
4,5 см2, тобто SB = 4,5. За другою з |
||||
|
|
|
|
|
|
|
|
формул (1.6) |
P(B) = 0,0625. |
|
||
Приклад 1.12. Два літаки прибувають у зону аеродрому в довільні моменти часу між 12-ю і 13-ю годинами. Посадка літака, що при-
14
був другим, може бути здійснена не раніше, ніж через 10 хв після |
||||||||
посадки першого. Знайти ймовірність того, що другому літаку не |
||||||||
доведеться чекати посадки. |
|
|
|
|
|
|
||
Розв’язання. Позначимо через x і |
y час прибуття в зону літаків |
|||||||
у межах від 12-ї до 13-ї години. Оскільки для x і y |
виконуються |
|||||||
умови 0 ≤ x ≤ 60, 0 ≤ y ≤ 60 , то простору елементарних наслідків Ω |
||||||||
відповідає квадрат на координатній площині зі стороною, що дорів- |
||||||||
нює 60 (рис. 1.2), тому SΩ = 3600. |
|
|
|
|
|
|||
Позначимо через B подію {другому літаку не доведеться чекати |
||||||||
посадки}. Сприятливими для цієї події є всі точки (x, |
y) , для яких |
|||||||
виконується умова |
x − y > 10 у межах квадрата Ω, або |
|
|
|||||
і |
|
x − y < −10 , звідки y > x + 10 |
|
|
||||
|
x − y > 10 , звідки |
y < x − 10 . |
|
|
||||
|
|
|
|
|||||
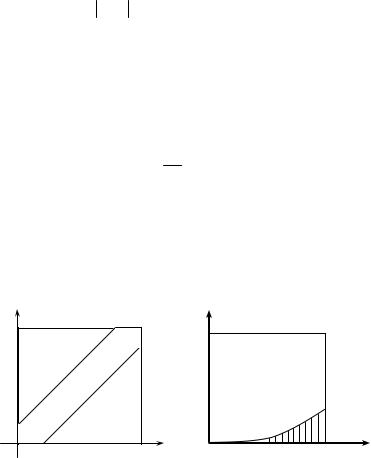
Ці умови задовольняють усі точки, що містяться в прямокутних |
||||||||
трикутниках, заштрихованих на рис.1.2, катети яких дорівнюють 50. |
||||||||
Отже, |
SB = 250 , а ймовірність P(B) |
обчислюється за другою фор- |
||||||
мулою (1.6): |
|
SB |
|
25 |
|
|
|
|
|
|
P(B) = |
= |
≈ 0,69. |
|
|
||
|
|
SΩ |
36 |
|
|
|||
|
|
|
|
|
|
|
||
Приклад 1.13. Два числа |
p i q навмання вибираються з відрізка |
|||||||
[0; 1]. Знайти ймовірність того, |
що рівняння x2 + px + q = 0 буде |
|||||||
мати дійсні корені одного знака. |
|
|
|
|
|
|||
Розв’язання. Випробування можна розглядати як вибір точки |
||||||||
( p, q) з квадрата OKLM (рис. 1.3) зі стороною, довжина якої дорів- |
||||||||
нює 1, тобто SΩ = 1. |
|
|
|
|
|
|
|
|
y |
|
|
|
|
q |
K |
|
|
60 |
|
Ω |
|
|
L |
|
||
|
y = x + 10 |
|
|
1 |
Ω |
|
|
|
|
|
|
|
|
|
|
||
10 |
y = x – 10 |
|
|
|
q = p2 / 4 |
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
О |
10 |
60 x |
|
О |
|
1 |
p |
|
|
Рис. 1.2 |
|
|
|
|
Рис. 1.3 |
|
|
|
|
|
|
|
|
|
|
15 |

Позначимо через C подію {корені рівняння дійсні й одного знака}. Сприятливими щодо події C є ті точки ( p, q) з квадрата Ω, для
яких виконуються умови:
p2 − 4q ≥ 0 (корені дійсні, отже, дискримінант рівняння D ≥ 0 ); q > 0 (корені одного знака, отже, їхній добуток q > 0 ).
Ці умови задовольняють усі точки області, заштрихованої на рис.1.3. Площу цієї області обчислимо інтегруванням:
SC = |
1 |
1 |
p2 dp = |
|
1 |
, |
4 |
∫ |
12 |
||||
|
|
0 |
|
|
|
|
а ймовірність події C за другою з формул (1.6) така: P(C) = 121 .
1.4. Відносна частота появи події та її стійкість. Статистичне означення ймовірності події
Класична формула (1.1) незастосовна, якщо простір Ω елементарних наслідків є нескінченна множина або немає достатніх під-
став вважати наслідки випробування ωi рівноможливими.
У цих випадках застосовують статистичне означення ймовірності події, яке ґрунтується на понятті відносної частоти події. Це поняття поряд з імовірністю належить до основних понять теорії
ймовірностей. |
|
|
Відносна частота W (A) |
події A — це відношення кількості μ |
|
випробувань, в яких подія |
A відбулась, до кількості ν всіх фактич- |
|
но проведених випробувань: |
|
|
|
W (A) = μ . |
(1.7) |
|
ν |
|
Різниця в означеннях імовірності події і відносної частоти полягає в тому, що для обчислення ймовірності за формулою (1.1) немає потреби проводити випробування, тобто ймовірність обчислюється апріорно, тоді як відносна частота може бути обчислена за формулою (1.7) лише після фактичного проведення випробувань.
Приклад 1.14. Авіакомпанія впродовж доби виконує 25 рейсів, із них 80 % — власним авіапарком. На час t було виконано 18 рейсів, із них 16 — власним парком. Знайти ймовірність і відносну частоту виконання рейсу власним парком.
16

Розв’язання. Позначимо подію A = {рейс виконується власним авіапарком}. Оскільки загальна добова кількість рейсів дорівнює 25, а власним парком виконується 20 рейсів (наслідки, сприятливі події A ), то ймовірність події A
P(A) = 2025 = 0,8 .
За умовою на час t було виконано 18 рейсів, тобто фактично проведено 18 випробувань, в яких подія A відбулась 16 раз. Отже, відносна частота події A
W (A) = 1618 = 0,89.
Тобто відносна частота W (A) може істотно відрізнятися від імовірності P(A) . Проте, як свідчать багаторазові дослідження, віднос-
ній частоті притаманна властивість стійкості, яка полягає в тому, що зі збільшенням кількості випробувань вона наближається до значення ймовірності події і відрізняється від нього тим менше, чим більше проведено випробувань. При цьому можуть спостерігатися окремі випадки, коли навіть при великій кількості проведених випробувань відносна частота W (A) істотно відрізняється від імовір-
ності події P(A) , проте загальна тенденція прямування відносної
частоти до ймовірності простежується досить закономірно.
Тому статистичною ймовірністю випадкової події A називають граничне значення відносної частоти події, до якого збігається за ймовірністю ця частота при необмеженому збільшенні кількості випробувань:
W (A) → P( A).
ν →∞
Т.1 ВПРАВИ ДЛЯ АУДИТОРНОЇ ТА САМОСТІЙНОЇ РОБОТИ
1.Знайдіть імовірність того, що навмання вибране двоцифрове натуральне число містить цифру 3.
2.Знайдіть імовірність того, що навмання вибране п’ятицифрове число однаково читається зліва направо і справа наліво.
3.Кинуто 2 гральні кубики. Знайдіть імовірності того, що:
а) кількість очок на першому кубику більша, ніж на другому; б) сума очок менша від п’яти; в) принаймні на одному кубику випаде 6 очок.
17
4.Яка ймовірність того, що навмання взяте натуральне число, яке не більше від 20, має 4 натуральні дільники?
5.Із множини чисел 0, 1, 2, ..., 9 навмання вибрано одне число q
іскладено рівняння x2 − 4x + q = 0.Знайдіть імовірність того, що ко-
рені рівняння: а) дійсні ірраціональні; б) комплексні.
6.У систему бронювання та продажу авіаквитків, в якій залишилось 6 квитків до Одеси, 4 до Львова і 2 до Донецька, надійшло замовлення на 5 квитків. Обчисліть імовірності того, що: а) замовлено квитки тільки до Одеси; б) замовлено 2 квитки до Одеси,
2до Львова і 1 до Донецька; в) не замовлено жодного квитка до Донецька.
7.Із комплекту, який містить 5 виробів, для перевірки їхньої якості 5 раз відбирають по одному виробу з поверненням перевіреного виробу до комплекту. Обчисліть імовірність того, що в результаті будуть перевірені всі вироби.
8.Цифри 1, 2, 3, ..., 9 записуються в ряд у довільному порядку. Знайдіть імовірність того, що: а) цифри 1 і 2 опиняться поряд; б) парні цифри займуть парні місця; в) сума цифр, які стоять на однаковій відстані від кінців ряду, дорівнює 10.
9.Сім літаків, серед яких два В-747, випадковим способом поставлено в чергу на технічне обслуговування. Знайдіть імовірність того, що між літаками В-747 опиняться 4 літаки інших типів.
10.Кожний із дванадцяти пасажирів може рівноможливо взяти квиток на один із чотирьох рейсів до Харкова. Знайдіть імовірності того, що: а) на перший рейс узяли квитки 3 пасажири; б) на кожний рейс узяли квитки по 3 пасажири; в) на один із рейсів узяли квитки 5 пасажирів, на другий — 4, на третій — 2 і на четвертий —
1пасажир.
11.Комплект містить 4 вироби вартістю 3 грн кожний, 3 вироби — по 2 грн і 2 вироби — по 1 грн. Знайдіть імовірність того, що навмання взяті 3 вироби коштують разом 7 грн.
12.Промінь локатора переміщується в горизонтальній площині зі
сталою кутовою швидкістю. Яка ймовірність того, що літак буде виявлено в кутовому секторі α радіан, якщо поява літака за будь-
яким напрямом однаково можлива?
13. Два числа x і y навмання вибираються з відрізка [0; 1]. Знайдіть імовірності того, що: а) x2 + y 2 ≤ 0,5; б) xy ≤ 0,9.
14. Дві особи домовились про зустріч між восьмою і дев’ятою годинами. Кожна з них приходить у довільний час, чекає 10 хв і залишає місце зустрічі. Яка ймовірність того, що вони зустрінуться:
а) не пізніше як о 8 год 30 хв; б) не раніше як о 8 год 55 хв?
18

15. На відрізку часу [0; 30 c] у довільний момент t1 з’являється сигнал тривалістю 5 с. Приймач умикається в довільний момент t2 на 10 с. Яка ймовірність виявлення сигналу приймачем?
16.Два довільні числа навмання вибрано з відрізка [0; 4]. Знайдіть імовірність того, що їхня сума не більша від чотирьох, а добуток не менший від трьох.
17.На площині взято два концентричні кола з радіусами r і R (r < R). Між колами навмання вибрано точку, через яку проведено
дотичні до меншого кола. Знайдіть імовірність того, що кут між дотичними буде меншим від α.
18.Стрижень довжиною 12 см навмання розламано на 3 частини. Знайдіть імовірність того, що з них можна скласти трикутник.
19.У кулю з радіусом R навмання кинуто точку. Обчисліть імо-
вірність потрапляння цієї точки у вписаний конус, твірна якого утворює з висотою кут α.
20.На кожній із трьох потокових ліній упродовж зміни виготовляється не більше як m приладів. Яка ймовірність того, що в наступну зміну сумарна кількість виготовлених приладів: а) буде більшою від m; б) буде в межах від m до 2m?
Відповіді
1. 0,2. 2. 0,01. 3. а) 5/12; б) 1/6; в) 11/36. 4. 0,25. 5. а) 0,2; б) 0,5. 6. а) 0,0075; б) 0,227; в) 0,318. 7. 0,0384. 8. а) 2/9; б) 1/126; в) 1/945. 9. 2/21.
10. а) 0,258; б) 0,022; в) 0,119. 11. 2/7. 12. α / 2π. 13. а) π / 8; |
б) 0,9(1– |
ln 0,9) . |
||||||
14. а) 5/36; б) 1/36. 15. 0,43. 16. (4 – 3 ln 3 )/16 ≈ 0,043. 17. |
|
2 |
sin |
2 α |
− r |
2 |
|
/ |
R |
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
/ (R2 − r2 )sin2 α2 . 18. 0,25. 19. 0,5 sin2 2α cos2 α. 20. а) 5/6; б) 2/3.
Т.1 ІНДИВІДУАЛЬНІ ТЕСТОВІ ЗАВДАННЯ
1.1.Обчисліть імовірності подій.
1.1.1.Комплект із 50 виробів містить 30 % нестандартних, причому 40 % нестандартних виробів є бракованими. Знайдіть імовірність того, що серед п’яти виробів, навмання взятих із комплекту, а) тільки 3 браковані; б) немає бракованих.
19
1.1.2.Вісім літаків, серед яких 2 літаки Ан-124, випадковим чином ставляться в чергу на технічне обслуговування. Знайдіть імовірність того, що між літаками Ан-124 у черзі опиняться три літаки інших типів.
1.1.3.Партія із 50 виробів містить 20 % браку. Із партії випадковим способом відбирають 6 виробів. Знайдіть імовірність того, що серед відібраних виробів: а) не буде бракованих; б) усі виявляться бракованими.
1.1.4.Дванадцять виробів, серед яких 4 нестандартні, випадковим способом розбито на дві рівні частини. Знайдіть імовірності того, що: а) в обох частинах буде однакова кількість нестандартних виробів; б) усі нестандартні вироби потраплять в одну частину.
1.1.5.До авіакаси звернулись 3 пасажири, кожний з яких рівноможливо замовляє квиток на один із шести рейсів, що виконуються протягом доби до аеропорту N. Знайдіть імовірність того, що вони замовлять квитки на різні рейси.
1.1.6.У лабораторії є 6 приладів з номерами від 1 до 6. Навмання по одному беруться всі прилади і послідовно включаються у схему. Знайдіть імовірність того, що у схемі номери розташуються у зростаючому порядку.
1.1.7.Десять однотипних виробів, що сходять з конвеєра, випадковим способом розподіляються по трьох контейнерах, у кожний з яких може потрапити будь-яка кількість цих виробів. Знайдіть імовірність того, що у перший контейнер потрапили 6 виробів, у другий — 3, а в третій — 1 виріб.
1.1.8.Із комплекту, який містить 9 приладів, відбираються будьякі 3 для ввімкнення у схему і після використання повертаються знову в комплект. Яка ймовірність того, що після трьох таких відборів буде використано всі прилади?
1.1.9.Комплект містить 7 виробів першого сорту, 6 — другого сорту і 2 — третього сорту. Випадковим способом одночасно з комплекту відібрано 5 виробів. Знайдіть імовірності того, що серед відібраних виробів: а) не буде виробів першого сорту; б) будуть вироби тільки першого сорту.
1.1.10.У касі придбано 5 авіаквитків для п’яти пасажирів і навмання роздано їм. Знайдіть імовірності того, що: а) усі пасажири одержали свої квитки; б) тільки три пасажири одержали свої квитки.
1.1.11.Комплект містить 5 виробів першого сорту, 4 — другого і 3 вироби третього сорту. Знайдіть імовірність того, що два випадково взяті вироби будуть одного сорту.
1.1.12.Із п’ятнадцяти рейсів, які здійснює авіакомпанія протягом доби, 60% виконуються власним літаковим парком. Знайдіть імовір-
20
