
Теорія ймовірності - high_math
.pdf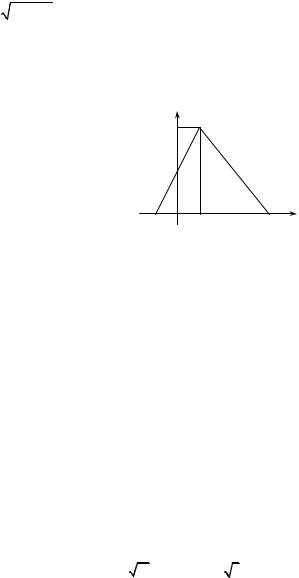
11. Неперервну випадкову величину Х задано функцією розподілу:
0,
F(x)= A x1,
|
|
|
x |
|
|
x ≤ −4, |
16 − x |
2 |
|
|
−4 < x ≤ 4, |
||
|
+ 16arcsin |
|
+ 8π |
, |
||
|
4 |
|||||
|
|
|
|
|
|
x > 4.
Знайти параметр А, математичне сподівання, дисперсію, середнє квадратичне відхилення та ймовірність того, що величина Х набуде
можливого значення з інтервалу (0; 2). |
|
|
|
|
|
|
|
|
|
|
|
12. Неперервну випадкову величину |
f(x) |
||||||||||
задано щільністю ймовірностей f (x), |
2/5 |
|
|
|
|
|
|
|
|
||
графік якої наведено на рис. 2.11. Запи- |
|
|
|
|
|
|
|
|
|
|
|
сати аналітичний вираз f (x) і знайти |
|
|
|
|
|
|
|
|
|
|
|
M(X), D(X), σ(X) цієї випадкової вели- |
|
|
|
|
|
|
|
|
|
|
|
чини. |
|
|
|
|
|
|
|
|
|
|
|
13. Для дискретної випадкової вели- |
–1 0 1 2 3 4 x |
||||||||||
чини Х із задачі 2 знайти початкові і |
|
|
Рис. 2.11 |
||||||||
центральні моменти до 3-го порядку. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
14. Для неперервної випадкової величини Х із задачі 10 знайти початкові і центральні моменти до 3-го порядку.
|
|
|
|
|
Відповіді |
|
|
|
|
|
|
|
|
|
|
|||
1. 1) p2 = 0, 2; p4 |
= 0,5. 3). а) 0,5 ; б) 0,2. |
|
|
|
|
|
|
|
|
|
|
|||||||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
– 3 |
|
1 |
|
2 |
|
2,5 |
|
|
|
|
|
|
||
|
|
|
Р |
0,6 |
|
0,2 |
|
0,1 |
|
0,1 |
|
|
|
|
|
|
||
а) 0,2; б) 0,9; в) 0,4. 3. |
M (X) =1,1; D( X ) = 1,09; |
σ(X) ≈1,044; |
Mo( X ) = 2. |
|||||||||||||||
4. M ( X ) = −1,15; D ( X ) = 5,3025; σ ( X ) ≈ 2,303; |
Mo( X ) = −3. |
5. |
p1 = 0,3; |
|||||||||||||||
p2 = 0, 2; p3 = 0,5; |
P{0 ≤ X ≤ 0, 2} = 0, 2. 6. x2 = −1; x3 = 0; |
p1 = 0, 4; |
||||||||||||||||
P{−2 ≤ X ≤ 0} = 0,9 . 7. |
M ( X ) = 0,15; |
D ( X ) = 0,1375; |
|
σ ( X ) ≈ 0,371; |
||||||||||||||
Mo ( X ) = 0. 8. |
M ( X ) = 1,5; D ( X ) = 0, 73; |
|
σ ( X ) ≈ 0,854; |
|
Mo ( X ) = 1 і 2. |
|||||||||||||
9. А = 2; M ( X ) |
= 16; D( |
X ) = |
44 |
; σ ( X ) = |
|
2 11 |
; Mo( X ) |
= |
2 3 |
; |
Me( X ) = |
|||||||
|
|
|||||||||||||||||
|
15 |
|
|
225 |
|
|
15 |
|
|
|
3 |
|
|
|
||||
91

= 4− 2 |
2 ≈ 1,08. 10. |
A = |
3 |
; M (X ) = 3; |
D( X) = 0,2; |
σ( X ) ≈ 0,447; Mo(X ) = 3; |
||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
16 − x |
2 |
, |
x |
−4; 4 , |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Me( X ) = 3. 11. À = 1 16π ; |
|
f (x) = |
|
|
|
|
[ |
|
] |
|
M(X) =0; D(X) = 4; |
|||||||||||||||
|
8π |
|
|
|
x [−4; 4]. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
x ≤ −1, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
+ 1 |
, |
|
−1 < x ≤ 1, |
||
|
|
|
|
|
|
= 3 |
3 + 2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
σ X |
|
= 2; |
P 0 < X < 2 |
|
≈ 0,304. 12. |
f |
|
x |
|
|
5 |
|
||||||||||||||
) |
|
( |
) |
= |
|
|
|
|
||||||||||||||||||
( |
|
{ |
} |
|
|
12π |
|
|
|
|
|
|
|
|
|
2 |
(4 − x) |
, 1 < x ≤ 4, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x > 4. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|||
M ( X ) = 4 ; |
|
19 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
D ( X ) = |
σ ( X ) ≈ 1, 027. 13. |
ν1 (X ) = −1,15; ν2 ( X ) = 6, 625; |
||||||||||||||||||||||||
|
|
|
3 |
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν3 ( X ) = −13,6375; μ1 |
= 0; |
μ2 |
= 5,3025; |
μ3 = 6,177. 14. ν1(X) = 3; |
ν2 ( X ) = 9,2; |
|||||||||||||||||||||
ν3 ( X ) = 28,8; |
μ1 = 0; |
μ2 = 0,2; |
μ3 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Т.1 ІНДИВІДУАЛЬНІ ТЕСТОВІ ЗАВДАННЯ
1.1. Знайдіть невідомі значення у рядах розподілу дискретних випадкових величин.
1.1.1. Дискретну випадковувеличину заданорядомрозподілу
X |
0 |
x2 |
2 |
3 |
P |
0,15 |
p2 |
0,45 |
p4 |
Знайдіть x2, p2, р4, якщо відомі математичне сподівання М(Х) = 1,6 і дисперсія D(X) = 0,84. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння даної випадкової величини в інтервал (0,5; 2).
1.1.2. Дискретну випадковувеличину заданорядомрозподілу
X |
–3 |
x2 |
0 |
x4 |
P |
p1 |
0,1 |
0,1 |
0,3 |
Знайдіть x2, x4 і р1, якщо x2 < x4 і відомі математичне сподівання М(Х)= – 0,5 і дисперсія D(X) = 9,45. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння даної випадкової величини в інтервал (–3; 1).
92

1.1.3. Дискретну випадкову величину задано рядом розподілу
|
|
Х |
|
x1 |
|
x2 |
– 1 |
1 |
|
|
|
|
Р |
|
0,1 |
|
0,3 |
p3 |
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Знайдіть x1 , x2 і |
p3 , якщо |
x1 < x2 |
і відомі математичне споді- |
|||||||
вання M ( X ) = −1, 2 |
і середнє квадратичне відхилення σ ( X ) = 1, 4. |
|||||||||
Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірністьпотраплянняданоївипадковоївеличинивінтервал(– 0,5; 1).
1.1.4. Дискретну випадкову величину задано рядом розподілу
|
X |
|
1 |
|
x2 |
|
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
0,2 |
|
p2 |
|
|
p3 |
0,2 |
|
|
|
|
|
|
|
|
||||
Знайдіть x2 , p2 і |
p3 |
, якщо відомі математичне сподівання |
||||||||
M (X )= 3,4 і дисперсія |
D ( X ) = 2,04. |
Побудуйте функцію розподі- |
||||||||
лу F(х) випадкової величини Х та знайдіть імовірність потрапляння даної випадкової величини у проміжок (0,5; 4].
1.1.5. Дискретну випадкову величину задано рядом розподілу
|
X |
|
– 0,2 |
|
– 0,1 |
|
|
0,1 |
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
0,5 |
|
0,3 |
|
|
p3 |
p4 |
|
|
Знайдіть x4 , |
p3 і p4 , |
|
якщо |
відомі |
математичне сподівання |
||||||
M ( X ) = −0,09 і дисперсія |
D ( X ) = 0,0249. |
Побудуйте функцію роз- |
|||||||||
поділу F(х) випадкової величини Х та знайдіть імовірність потрапляння даноївипадковоївеличиниу проміжок(– 0,15; 0,1].
1.1.6. Дискретну випадкову величину задано рядом розподілу
|
X |
x1 |
|
– 0,1 |
|
0,2 |
x4 |
|
|
P |
0,3 |
|
p2 |
|
0,4 |
0,2 |
|
Знайдіть x1 , x4 |
і p2 , якщо |
x1 < x4 |
|
і відомі математичне споді- |
||||
вання M (X )= 0,09 |
і дисперсія D(X ) = 0,0529. Побудуйте функцію |
|||||||
розподілу F(х) випадкової величини Х та знайдіть імовірність потраплянняданоївипадковоївеличиниу проміжок(– 0,1; 0,4].
93

1.1.7. Дискретну випадкову величину задано рядом розподілу
|
|
X |
|
– 1 |
– 0,5 |
0,5 |
|
2 |
|
|
|
P |
|
0,2 |
p2 |
p3 |
|
p4 |
|
|
|
|
|
|
|
||||
Знайдіть |
p2 , p3 |
і p4 , якщовідоміматематичнесподівання M(X )= 0,7 |
|||||||
і дисперсія |
D(X ) |
= 1,41. Побудуйте функцію розподілу F(х) випадко- |
|||||||
вої величини Х та знайдіть імовірність потрапляння даної випадкової величиниупроміжок[– 0,5; 0,4].
1.1.8. Дискретну випадкову величину задано рядом розподілу
|
X |
– 0,5 |
x2 |
|
1 |
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
P |
p1 |
0,2 |
|
0,1 |
0,1 |
|
|
|
|
|
|
|
|
|||
Знайдіть x2 , x4 і |
p1 , якщо x2 < x4 |
і відомі математичне сподіван- |
||||||
ня M (X )= 0,1 і дисперсія D(X )= 0,69. Побудуйте функцію розподі-
лу F(х) випадкової величини Х та знайдіть імовірність потрапляння даної випадкової величини у проміжок [– 0,2; 0,4].
1.1.9. Дискретну випадкову величину задано рядом розподілу
|
X |
|
– 6 |
|
x2 |
– 2 |
|
– 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
0,1 |
|
p2 |
p3 |
|
0,3 |
|
|
Знайдіть x2 , |
p2 і |
p3 , |
якщо відомі математичне сподівання |
|||||||
M ( X ) = −2,6 і дисперсія |
D ( X ) = 2, 45. |
Побудуйте функцію розподілу |
||||||||
F(х) випадкової величини Х та знайдіть імовірність потрапляння цієї величиниу проміжок[–5,5; –2].
1.1.10. Дискретну випадкову величину задано рядом розподілу
|
X |
|
x1 |
0 |
x3 |
|
3 |
|
|
P |
|
ð1 |
0,2 |
0,1 |
0,2 |
|
|
|
|
|
|
|
||||
Знайдіть x1, x3 |
і p1, якщо відомі математичне сподівання M(X) =−0,3 |
|||||||
і дисперсія D( X )= 3,81. Побудуйте функцію розподілу F(х) випадко-
вої величини Х та знайдіть імовірність потрапляння даної випадкової величиниупроміжок[1,5; 3].
94
1.1.11. Дискретну випадкову величинузаданорядомрозподілу
X |
0,5 |
1 |
1,7 |
x4 |
P |
0,1 |
0,2 |
p3 |
p4 |
Знайдіть x4, p3, р4, якщо відомі математичне сподівання М(Х) = 1,56 і дисперсія D(X) = 0,2584. Побудуйте функцію розподілу F(х) величини Х та знайдіть імовірність потрапляння цієї величини у промі-
жок (1,2; 1,7].
1.1.12. Дискретну випадкову величинузаданорядомрозподілу
X |
0 |
x2 |
2 |
3 |
P |
0,15 |
p2 |
0,45 |
p4 |
Знайдіть x2, p2, р4, якщо відомі математичне сподівання М(Х) = 1,6 і дисперсія D(X) = 0,84. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння даної випадкової величиниу проміжок(1,5; 3].
1.1.13. Дискретну випадкову величинузаданорядомрозподілу
X |
–3 |
x2 |
0 |
x4 |
P |
p1 |
0,1 |
0,1 |
0,3 |
Знайдіть x2, x4 і р1, якщо x2 < x4 і відомі математичне сподівання M ( X ) = − 0,5 і дисперсія D(X) = 9,45. Побудуйте функцію розподілу
F(х) випадкової величини Х та знайдіть імовірність потрапляння даної випадковоївеличиниу проміжок[–3; 1).
1.1.14. Дискретну випадкову величинузаданорядомрозподілу
X |
x1 |
x2 |
0,5 |
2 |
P |
0,2 |
0,3 |
p3 |
0,1 |
Знайдіть x1, x2 і р3, якщо x1 < x2 і відомі математичне сподівання М(Х) = 0,05 і дисперсія D(X) = 0,7725. Побудуйте функцію розподілу F(х) величини Х та знайдіть імовірність потрапляння цієї випадкової величини в інтервал (1,5; 2).
1.1.15. Дискретну випадкову величинузаданорядомрозподілу
X |
1 |
2 |
x3 |
x4 |
P |
p1 |
0,2 |
0,3 |
0,1 |
95
Знайдіть x3, x4 і р1, якщо x3 < x4 і відомі математичне сподівання М(Х) = 2,6 і дисперсія D(X) = 2,84. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння цієї величиниу проміжок[1; 2,5).
1.1.16. Дискретну випадкову величинузаданорядомрозподілу
X |
x1 |
– 1 |
x3 |
2 |
P |
0,1 |
p2 |
0,4 |
0,3 |
Знайдіть x1, x3 і р2, якщо x1 < x3 і відомі математичне сподівання М(Х) = 0,2 і дисперсія D(X) = 1,76. Побудуйте функцію розподілу F(х) величини Х та знайдіть імовірність потрапляння цієї величини у промі-
жок(1; 2].
1.1.17. Дискретну випадкову величинузаданорядомрозподілу
X |
x1 |
1 |
3 |
x4 |
P |
0,2 |
0,4 |
p3 |
0,3 |
Знайдіть x1, x4 і р3, якщо x1 < x4 і відомі математичне сподівання М(Х) = 2 і дисперсія D(X) = 5. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння цієї величини у проміжок(0,5; 3].
1.1.18. Дискретну випадкову величинузаданорядомрозподілу
X |
1 |
x2 |
1,5 |
x4 |
P |
p1 |
0,1 |
0,4 |
0,2 |
Знайдіть x2, x4 і р1, якщо x2 < x4 і відомі математичне сподівання М(Х) = 1,27 і дисперсія D(X) = 0,3961. Побудуйте функцію розподілу F(х) величини Х та знайдіть імовірність потрапляння цієї величини у проміжок[1; 1,7).
1.1.19. Дискретну випадкову величинузаданорядомрозподілу
X |
0 |
x2 |
2 |
x4 |
P |
0,15 |
0,25 |
p3 |
0,15 |
Знайдіть x2, x4 і р3, якщо x2 < x4 і відомі математичне сподівання М(Х) = 1,6 і дисперсія D(X) = 0,84. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння цієї величиниу проміжок(0,2; 2].
96
1.1.20. Дискретну випадкову величинузаданорядомрозподілу
X |
x1 |
x2 |
1 |
2 |
P |
0,2 |
0,4 |
0,3 |
p4 |
Знайдіть x1, x2 і р4, якщо x1 < x2 і відомі математичне сподівання М(Х) = – 0,3 та дисперсія D(X) = 1,81. Побудуйте функцію розподілу F(х) та знайдіть імовірність потрапляння величини Х у проміжок
[– 0,5; 1].
1.1.21. Дискретну випадкову величинузаданорядомрозподілу
X |
0 |
1 |
x3 |
x4 |
P |
0,1 |
p2 |
0,4 |
0,2 |
Знайдіть x3, x4 і р2, якщо x3 < x4 і відомі математичне сподівання М(Х) = 0,96 та дисперсія D(X) = 0,15. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння цієї величиниу проміжок[0; 1,5).
1.1.22. Дискретну випадкову величинузаданорядомрозподілу
X |
x1 |
– 1 |
x3 |
5 |
P |
0,3 |
p2 |
0,1 |
0,4 |
Знайдіть x1, x3 і р2, якщо x1 < x3 і відомі математичне сподівання М(Х)=1,1 та дисперсія D(X) = 12,09. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння цієї величиниу проміжок[–1; 3].
1.1.23. Дискретну випадкову величинузаданорядомрозподілу
X |
– 1 |
x2 |
x3 |
0 |
P |
0,4 |
0,3 |
p3 |
0,1 |
Знайдіть x2, x3 і р3, якщо x2 < x3 і відомі математичне сподівання М(Х) = – 0,57 і середнє квадратичне відхилення σ(X) = 0,39. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потраплянняцієївеличиниу проміжок[– 1; – 0,5].
1.1.24. Дискретну випадкову величинузаданорядомрозподілу
X |
0 |
x2 |
2 |
3 |
P |
0,729 |
p2 |
0,027 |
p4 |
97
Знайдіть x2, p2, р4, якщо відомі математичне сподівання М(Х) = 0,3 і дисперсія D(X) = 0,27. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння цієї величини у промі-
жок(0,5; 2].
1.1.25. Дискретну випадкову величинузаданорядомрозподілу
X |
x1 |
– 0,5 |
– 0,1 |
0 |
P |
p1 |
0,3 |
0,2 |
p4 |
Знайдіть x1, р1, p2, якщо відомі математичне сподівання М(Х) = –0,57 і середнє квадратичне відхилення σ(X) = 0,39. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння цієївеличиниу проміжок[–0,6; –0,1].
1.1.26. Дискретну випадкову величинузаданорядомрозподілу
X |
–5 |
x2 |
3 |
4 |
P |
p1 |
0,3 |
p3 |
0,2 |
Знайдіть x2, p1, р3, якщо відомі математичне сподівання М(Х) = – 0,3 і середнє квадратичне відхилення σ(X) = 3,9. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння цієївеличиниу проміжок(0; 3].
1.1.27. Дискретну випадкову величину заданорядомрозподілу
X |
1,5 |
x2 |
x3 |
4,5 |
P |
0,4 |
0,3 |
p3 |
0,1 |
Знайдіть x2, x3 і p3, якщо x2 < x3 і відомі математичне сподівання М(Х) = 2,5 і середнє квадратичне відхилення σ(X) = 1. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потраплянняцієївеличиниупроміжок[3; 4,5].
1.1.28. Дискретну випадкову величинузаданорядомрозподілу
X |
–3,2 |
x2 |
0,4 |
4,9 |
P |
p1 |
0,25 |
p3 |
0,3 |
Знайдіть x2, p1 і р3, якщо відомі математичне сподівання М(Х)=
= 0,53 і дисперсія D(X) = 9,6501. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння цієї величини упроміжок[–1; 0,4].
98

1.1.29. Дискретну випадкову величинузаданорядомрозподілу
X |
x1 |
4 |
6 |
x4 |
P |
0,2 |
p2 |
0,4 |
0,2 |
Знайдіть x1, x4, і p2, якщо x1 < x4 і відомі математичне сподівання М(Х) = 7,6 і середнє квадратичне відхилення σ(X) = 4,8. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть iмовірність потраплянняцієївеличиниупроміжок(3; 6].
1.1.30. Дискретну випадкову величинузаданорядомрозподілу
X |
x1 |
–1 |
0 |
x4 |
P |
0,5 |
0,2 |
0,1 |
p4 |
Знайдіть x1, x4 і p4, якщо x1 < x4 і відомі математичне сподівання М(Х) = –1 і дисперсія D(X) = 1,4. Побудуйте функцію розподілу F(х) випадкової величини Х та знайдіть імовірність потрапляння цієї величини упроміжок[–1; 0,5].
1.2. Неперервну випадкову величину Х задано функцією розподілу F (x) (щільністю ймовірності f (x) ). 1) Визначте параметр А; 2) знай-
діть щільність імовірності f (x) (функцію розподілу F (x) ); 3) побудуйте графіки функцій F (x) і f (x); 4) знайдіть числові характеристики M(X), D(X), σ(X) ; 5) обчисліть імовірність того, що випадкова величина Х у результаті випробування набуде можливого значення із заданого інтервалу (α; β).
0, |
|
x ≤ 1, |
|
1.2.1. F (x)= |
Aln x, |
1 < x ≤ e, |
|
|
1, |
|
x > e. |
|
|
||
0, |
|
x ≤ 1, |
|
1.2.2. F (x)= |
A |
(1− 1 x2 ), 1 < x ≤ 2, |
|
|
1, |
|
x > 2. |
|
|
||
0, |
|
x ≤ 0, |
|
1.2.3. F (x)= |
Asin x, |
0 < x ≤ π 2, |
|
|
1, |
|
x > π 2. |
|
|
||
(e / 3; e / 2).
(1,2; 1,7).
(π 4; π
4; π 3).
3).
99

0, |
(x2 + x − 2), |
x ≤ 1, |
||
1.2.4. F (x)= |
A |
1 < x ≤ 2, |
||
|
1, |
|
|
x > 2. |
|
|
|
||
0, |
|
x ≤ 0, |
||
1.2.5. F (x)= |
Asin2 x, |
0 < x ≤ π 3, |
||
|
1, |
|
x > π 3. |
|
|
|
|||
0, |
|
|
x ≤ 0, |
|
1.2.6. F (x)= |
A(x − sin x), |
0 < x ≤ 2π, |
||
|
1, |
|
|
x > 2π. |
|
|
|
||
0,
1.2.7. F (x)= Ax x,
1,
0,
1.2.8. F (x)= Acos x,
1,
0,
1.2.9. F (x)= A3 x,
1,
0,
1.2.10. F (x)= A 5 x2 ,
1,
x ≤ 0,
0 < x ≤ 4, x > 4.
x ≤ − π 2,
− π 2 < x ≤ 0, x > 0.
x ≤ 0,
0 < x ≤ 8,
x> 8.
x≤ 0,
0 < x ≤ 1, x > 1.
|
0, |
|
|
|
|
|
|
x ≤ −3, |
|||
|
|
|
|
π |
|
|
x |
|
|
|
|
1.2.11. |
F (x)= |
A |
|
+ arcsin |
|
|
, |
−3 < x ≤ 3, |
|||
3 |
|||||||||||
|
|
|
|
2 |
|
|
|
|
x > 3. |
||
|
1, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
x ≤ 0, |
|
|
||||||
1.2.12. |
f (x) = |
|
|
A |
, |
0 < x ≤ e − 1, |
|||||
1+ x |
|||||||||||
|
|
|
x > e − 1. |
|
|||||||
|
|
1, |
|
|
|
||||||
(1,5; 1,8).
(π 6; π
6; π 4).
4).
(π 2; π).
2; π).
(1; 2,25).
(− π 3; − π
3; − π 6).
6).
(1; 8).
(1/32; 1).
(0; 1,5).
(0; 1).
100
