Универсальные множества и операция дополнения
В некоторых случаях все множества, участвующие в математических рассуждениях, содержатся в одном множестве U, которое называется универсальным множеством или универсумом.
Например, в школьной планиметрии рассматривались точки, прямые и фигуры, являющиеся подмножествами фиксированной плоскости, которую и можно считать универсальным множеством. Специалист по математическому анализу, как правило, работает в пространстве Rn, которое для него является универсумом.
Если U
– универсальное
множество, то все объекты и множества
их содержатся в U,
так что высказывания x
U,
а также A
U
для любых
элементов x
и множеств
A
являются
тождественно истинными, а высказывания
x
U
и A
U
–
тождественно
ложными.
При наличии универсального множества определена ещё одна операция над множествами:
Если U – универсальное множество, А U, то дополнением множества А называется множество
=U
\ А.
Ясно, что операция
дополнения является частным случаем
операции разности множеств. При этом
x
x
U
\ А
x
U
x
A
1
x
A
x
A.
Примеры: 1.
Пусть U
= R,
A
= (–5; 2]
(3; +∞).
Изобразим
на числовой оси множество
=
(–∞; –5]
(2; 3]:
2. В коробке лежат шары: 10 красных, 8 белых и 5 чёрных. Какое наименьшее количество шаров нужно вытащить из коробки, чтобы среди них наверняка оказалось 3 красных ?
Пусть U
– множество
всех шаров в коробке, А
– множество
красных шаров. Тогда
–множество
остальных (белых или чёрных) шаров, и
количество элементов в
равно 13
(= 8+5).
Каждый вытащенный из коробки шар
принадлежит либо множеству А,
либо множеству
,
поэтому, вытащив первые 13
шаров нельзя быть уверенным, что среди
них есть хотя бы один красный. Зато,
вытащив ещё 3
шара, можно
наверняка утверждать, что среди этих
16-ти
шаров 3
окажутся
красными. Таким образом, нужно вытащить
16
шаров.
Упражнения: 1. Почему в предыдущем примере недостаточно вытащить 15 шаров ?
2. Какое наименьшее количество шаров (в условиях примера 2) нужно вытащить из коробки, чтобы среди них наверняка оказалось 3 красных и один белый ?
§ 2. Проверка некоторых равенств со множествами
В этом параграфе будет более подробно рассказано о том, как проверять равенства множеств. Хорошим наглядным средством для этого служат диаграммы Эйлера-Венна, на которых множества условно изображаются в виде геометрических фигур на плоскости (как правило, в виде кругов). Это даёт возможность наглядно представить себе процесс построения более сложных множеств из простых с помощью изученных в предыдущем параграфе основных операций над множествами.
Пример. Ниже представлены диаграммы Эйлера-Венна для множеств A B, A B, A \ B, B \ A, A (B C), (A B) (A C):
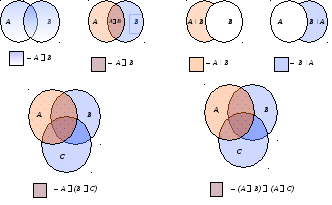
Эти диаграммы наводят на мысль, что последние два множества должны совпадать: A (B C) = (A B) (A C). Однако такое зрительное восприятие не является доказательством равенства множеств, оно лишь может помочь заметить это равенство. Чтобы получить формальное доказательство равенства указанных множеств, нужно, следуя определению, доказать, что для любого x верно x A (B C) x (A B) (A C). Это можно сделать, следуя приводимому ниже общему алгоритму:
расписываем все отношения принадлежности в левой и правой частях доказываемой эквивалентности, следуя формальному определению операций над множествами:
x A (B C) (x A) (x B C) (x A) (x B x C),
x (A B) (A C) x (A B) x (A C)
(x A x B) (x A x C).
Таким образом,
левая и правая части доказываемой
эквивалентности записаны через
элементарные высказывания вида x
Y
и их отрицания
x
Y
с помощью логических связок.
для участвующих в полученных записях элементарных высказываний введём буквенные обозначения: так, в рассматриваемом конкретном случае, обозначим a = (x A), b = (x B), c = (x C), сведя доказательство к проверке истинности формулы a (b c) (a b) (a c).
равенство множеств имеет место тогда и только тогда, когда полученная формула будет законом логики: в рассматриваемом случае это закон дистрибутивности. Следовательно, рассматриваемое равенство множеств A (B C) = (A B) (A C) доказано.
В дальнейшем будут приведены другие примеры доказательств равенств множеств.
Если же на диаграммах Эйлера-Венна получаются заведомо разные рисунки множеств, то равенство множеств не выполнено, т.к. оно нарушается уже в частном случае фигур на плоскости. Например, A \ B B \ A, что видно из построенных выше диаграмм Эйлера-Венна для множеств A \ B и B \ A.
Теорема (об основных равенствах множеств). (I) Для любых множеств A, B, C справедливы следующие равенства:
(1) A = A (закон тождества),
(2) A A = A (идемпотентность пересечения),
A A = A (идемпотентность объединения),
(3) A B = B A (коммутативность пересечения ),
A B = B A (коммутативность объединения),
(4) (A B) C = A (B C) (ассоциативность пересечения),
(A B) C = A (B C) (ассоциативность объединения),
(5) (A B) C = (A С) (B C) (законы дистрибутивности
(A B) C = (A С) (B C) пересечения и объединения),
(6) A \ (B \ C) = (A \ B) (A C),
(7) (A \ B) \ C = (A \ C) \ B = A \ (B C),
(8) A = (A B) (A \ B) и (A B) (A \ B) = ,
(9) A \ (B C) = (A \ B) (A \ C),
A \ (B C) = (A \ B) (A \ C),
(10) (A B) \ C = (A \ C) (B \ C),
(A B) \ C = (A \ C) (B \ C),
(11) A \ A = , A = A, A = .
(II) Если U – универсальное множество, то для любых множеств А и В справедливы равенства:
(12) A U = U, A U = A,
(13) A
= ,
A
= U,
(14) 
= A,
(15) 
=
,
=
(16) A
B
тогда и только тогда, когда
.
Доказательство. Докажем лишь некоторые равенства, оставляя остальные в качестве упражнений.
(
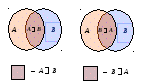3)A
B
= B
A.
Вначале
строим диаграмму Эйлера-Венна, которая
подтверждает правдоподобность
доказываемого равенства.
Теперь докажем формально: нужно доказать, что x A B x B A. Имеем:
x A B (x A) (x B), x B A (x B) (x A),
и обозначая а = (x A), b = (x B), приходим к формуле a b b a, которая является законом логики (закон коммутативности конъюнкции).
Равенство множеств A B = B A доказано.
(8) A = (A B) (A \ B), (A B) (A \ B) = . Строим диаграмму Эйлера-Венна, которая подтверждает правдоподобность доказываемых равенств.
Т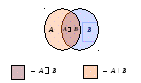
еперь
докажем первое равенство: нужно доказать,
чтоx
A
x
(A
B)
(A
\ B).
x (A B) (A \ B)
(x A B) (x A \ B)
(x
A
x
B)
(x
A
).
Таким образом,
обозначив a
= (x
A),
b
= (x
B),
получим формулу a
(a
b)
(a
),
которая является законом логики: (a
b)
(a
)
a
(b
)
a
1
a.
Равенство множеств A
= (A
B)
(A
\ B)
доказано.
Для доказательства второго равенства (A B) (A \ B) = нужно лишь учесть, что по определению пустого множества, высказывание x тождественно ложно. Таким образом, остаётся доказать, что x (A B) (A \ B) 0. Это делается по стандартной схеме:
x (A B) (A \ B) (x A B) (x A \ B)
(x
A
x
B)
(x
A
x
B)
(a
b)
(a
)
a
b
a
a
a
b
a
0
0.
Утверждение (8) доказано.
(9) A \ (B C) = (A \ B) (A \ C). Строим диаграммы Эйлера-Венна, которые подтверждают правдоподобность доказываемого равенства.
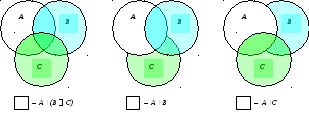
Формальное доказательство проводится стандартно: для проверки истинности формулы x A \ (B C) x (A \ B) (A \ C) перепишем её левую и правую части, используя определения операций над множествами:
x
A \ (B
C)
x
A
x
A
a
,
x (A \ B) (A \ C) (x A \ B) (x A \ C)
(x
A
x
B)
(x
A
x
C)
(a
)
(a
).
Остаётся проверить,
что формула a
(a
)
(a
)
является
законом логики. Это следует из законов
ассоциативности, коммутативности,
идемпотентности и законов де Моргана:
a
a
(
)
a
a
(a
)
(a
).
Равенство A \ (B C) = (A \ B) (A \ C) доказано.
Все утверждения п. (II) теоремы можно вывести из уже доказанных равенств п. (I).
(12) A U = A. В самом деле,
A = (A U) (A \ U) = (A U) = A U.
Здесь использовано равенство A \ U = , которое легко следует из того, что А U: x A \ U x A x U x A 0 0 x .
(14)
=
A.
Действительно,
= U
\
=U
\ (U
\ A) = (U
\ U)
(U
A) =
A = A.
(16) Если
A
B,
то x
A
x
B
– тождественно
истинное высказывание. Докажем, что
,
т.е. что высказывание x
x
тоже
тождественно истинно. Пусть, как обычно,
a
= (x
A),
b
= (x
B).
Тогда x
x
B
,
x
и по закону
контрапозиции получаем x
x
(
)
(a
b)
1,
что и требовалось.
Если наоборот
,
то по уже доказанному,
,
т.е. A
B,
что и требовалось.
Теорема доказана.