Модуль 2. Економетрика
Змістовий модуль 2. Різні аспекти економетричного моделювання
Тема 3. Нелінійні моделі та перетворення змінних
Мета : ознайомити студентів з перетвореннями змінних в нелінійних
однофакторних та багатофакторних регресійних моделях та особливостями
визначення їх параметрів.
План вивчення теми
1.Перетворення змінних у випадку квазілінійної парної регресії.
2.Перетворення змінних у випадку нелінійної відносно змінних та параметрів парної регресії.
3.Перетворення змінних у випадку квазілінійної множинної регресії.
4.Перетворення змінних у випадку нелінійної відносно змінних та параметрів багатофакторної регресії.
5.Особливості визначення меж довірчого інтервалу прогнозу у випадках різних типів нелінійностей.
Методичні рекомендації до самостійної роботи
Найпростіші перетворення нелінійних парних моделей в лінійні
Тільки в окремих випадках використовуються лінійні моделі. Зазвичай на
практиці ми стикаємося з випадками суттєвих нелінійностей, при яких немає
сенсу використовувати лінійні |
функції |
для апроксимації вихідних , даних |
оскільки ніяка лінійна регресія у цьому випадку не буде адекватною. У таких |
||
випадках використовують різні нелінійні функції. Вид функції (тренда) можна |
||
підібрати згідно з розподілом |
даних |
спостережень за допомогою майстра |
діаграм в EXCEL. Далі для визначення параметрів нелінійної регресії методом
найменших квадратів функцію треба звести до лінійного вигляду. Це можна зробити завдяки математичним перетворенням таким, як логарифмування та заміна змінних. Для логарифмування використовують математичну функцію
30
LN. Далі для лінеарізованої моделі застосовують метод найменших квадратів,
як було показано вище.
Розглянемо загальний випадокквазілінійної парної регресії, тобто регресії, лінійної відносно параметрів:
yi = a0 + a1j(xi ) + li .
Заміною змінної |
zi |
= j(xi ), i = 1...n |
нелінійна парна модель зводиться |
|||||||||||||
до лінійної: |
yi = a0 + a1zi |
+ li . Формули для оцінки параметрів регресії мають |
||||||||||||||
|
|
|
n |
n |
n |
|
|
|
|
|
|
n |
n |
|
||
|
|
nå zi yi - å zi å yi |
|
|
|
|
|
|
å yi - ai å zi |
|
||||||
вигляд: |
a = |
|
i=1 |
i=1 |
i=1 |
, |
|
a |
0 |
= |
|
i=1 |
i=1 |
. |
(23) |
|
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||
|
1 |
|
n |
æ |
n |
ö2 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
nå zi2 - çç |
å zi ÷÷ |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
i=1 |
è i=1 |
ø |
|
|
|
|
|
|
|
|
|
|
|
Коефіцієнт еластичності обчислюється за формулою: |
|
|
|
|||||||||||||
|
|
|
|
K e |
= a j / (x) |
|
|
xi |
|
. |
|
|
(24) |
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
xi |
1 |
|
|
yiроз. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Параметри регресії підставляються у початкову модель, для оцінки адекватності якої користуються критерієм Фішера таким же чином, як описано вище.
Точкову оцінку прогнозу можна обчислити за формулою:
y роз. = a |
0 |
+ a z |
пр |
. |
|
|
|
|
|
(25) |
||||
пр |
|
|
1 |
|
|
|
|
|
|
|
||||
Довірчий інтервал ( yпрроз. - Dyпр ; yпрроз. + Dyпр ) |
будуємо згідно з формулою: |
|||||||||||||
|
|
|
|
|
|
|
||||||||
Dyпр = tкрит S 1 + |
1 |
+ |
(zпр - z )2 |
|
||||||||||
|
|
|
|
|
|
|
. |
(26) |
||||||
|
n |
n |
|
|
|
|||||||||
|
|
|
|
å(zi |
- |
z |
)2 |
|
|
|
||||
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
Довірчу зону утворюють довірчі інтервали для всіх базисних даних. Для кожного спостереження (базисного даного) будують довірчий інтервал за аналогічною формулою. Спочатку треба знайти точкову оцінку, тобто розрахункове значення, показника для даного спостереження:
yiроз. = a0 + a1 zi . |
(27) |
31
Далі обчислюємо Dyi :
|
|
|
|
Dyi = tкрит S |
1 + |
1 |
+ |
(zi |
- |
z |
)2 |
. |
|
|
|
|
|
|
(28) |
|
|||||||
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
å(zi - |
z |
)2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким |
чином, |
розраховуємо |
|
|
|
|
границі |
|
довірчого |
інтервал |
|||||||||||||||||
( yiроз. - Dyi ; yiроз. + Dyi ) для кожного спостереження. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Цікавим є |
випадокпоказникової |
|
однофакторної |
регресії, нелінійної |
|
||||||||||||||||||||||
відносно параметрів, яка має рівняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
y роз = a xa1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(29) |
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Спочатку треба прологарифмувати рівняння: |
|
ln y роз = ln a |
0 |
+ a ln x . |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
Тепер можна зробити заміну змінних: |
ln y роз |
= y |
роз , |
ln a |
0 |
= a |
01 |
, |
ln x = z . |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
При цьому |
можна користуватися функцієюLN. |
|
|
|
Модель |
набуде |
вигляду: |
|
|||||||||||||||||||
y ðîç . = a |
01 |
+ a z . |
Очевидно, це рівняння парної лінійної регресії. Параметри |
|
|||||||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лінійної |
моделі a01, a1 оцінюємо, як |
було |
|
|
описано |
|
вище. |
|
Щоб |
|
отримати |
|
|||||||||||||||
значення |
параметру a0 , треба зробити |
наступні перетворення: a0 = exp(a01) . |
|
||||||||||||||||||||||||
Можна для цього використати функцію EXP. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Отримані параметри підставляють у вихідне нелінійне рівняння. За тим |
|
||||||||||||||||||||||||||
же рівнянням можна обчислити розрахункові значення для базисних даних, |
|||||||||||||||||||||||||||
середнє значення показника та точкову оцінку прогнозного значення показника. |
|
||||||||||||||||||||||||||
Модель перевіряють на адекватність за критерієм Фішера. Розрахункове |
|
||||||||||||||||||||||||||
значення критерію отримують за формулою: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F = |
å( yi роз - |
y |
)2 /1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
(30 |
|
|||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
å( yi - yi роз |
)2 /(n - 2) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
s =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коефіцієнт еластичності обчислюється таким чином:
32
e |
xi |
|
|
|
K xi = a0a1 |
|
. |
(31) |
|
yiроз. |
||||
|
|
|
||
Довірчий інтервал визначають спочатку для лінеарізованої моделі y1 – z |
||||
за відповідними формулами: ( y1прроз. - Dy1пр ; y1прроз. + Dy1пр ), де Dy1пр |
обчислюється |
|||
за формулою: |
|
|
|
|
Dy1пр |
= t |
крит S 1 + |
1 |
+ |
(zi |
- |
z |
)2 |
. |
(32) |
||
n |
n |
|
||||||||||
|
|
|
|
å(zi - |
z |
)2 |
|
|
||||
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
Потім за допомогою обернених перетворень(потенціювання) меж надійного інтервалу лінійної регресії визначають межінадійного інтервалу показникової регресії:
yпрроз. - Dyпр = exp( y1прроз. - Dy1пр ); |
yпрроз. + Dyпр =exp( y1прроз. + Dy1пр ). |
(33) |
Очевидно, за таких перетворень межі довірчого інтервалу будуть несиметричними відносно розрахункового прогнозного значення показника.
Перетворення багатофакторних нелінійних економетричних
моделей
За допомогою математичних перетворень, як то заміна змінних та
логарифмування нелінійні моделі від декількох факторів або |
від одного у |
||
випадку поліноміальної функції , можна звести до лінійних багатофакторних, |
|||
для оцінок параметрів яких вже можна застосовувати звичайний МНК. |
|
||
Також, як |
і в |
парних регресіях, розрізняють нелінійність |
відносно |
факторів (квазілінійність) та параметрів. |
|
||
Наприклад, |
якщо |
в нелінійній квадратичній моделі, яка |
визначає |
залежність показника від одного фактора, |
|
||
y = a |
0 |
+ a X + a |
2 |
X 2 |
(34) |
|
1 |
|
|
||
ввести заміну змінної X 2 = Z , можна отримати двофакторну лінійну регресію: |
|||||
y = a0 + a1 X + a2Z . |
(35) |
||||
Далі застосовують алгоритм, який описано вище для множинної регресії.
33
Практичним застосуванням множинної нелінійної моделі виробничіє
функції, наприклад, мультиплікативна |
функція |
типу |
Кобба-Дугласа. |
Виробнича функція відображає залежність випуску від витрат ресурсів. |
|||
Мультиплікативна функція типа Кобба-Дугласа має вигляд: |
|
||
Y = a0 X1a1 X 2a 2 , |
|
|
(36) |
де Y – обсяг випущеної продукції; |
|
|
|
X1 – основні засоби підприємства; |
|
|
|
X 2 – працезатрати; |
|
|
|
a0 , a1 , a2 – параметри моделі. |
|
|
|
Особливим випадком мультиплікативної функції є |
функція - Кобба |
||
Дугласа. Вона має такий само вигляд, але для неї виконується умова: |
|
||
a1 + a2 =1. |
|
|
|
Мультиплікативна функція застосовується для моделювання на макро- і
мікрорівнях.
Для визначення параметрів моделі можна застосувати метод найменших
квадратів. Для цього нелінійну модель треба звести до лінійної форми. Після логарифмування
ln Y = ln a0 + a1 ln X1 + a2 ln X 2 |
(37) |
і заміни змінних Y1 = ln(Y ) , Z1 = ln(X1 ) Z2 = ln(X 2 ) , |
отримаємо приведену |
лінійну регресію: |
|
Y1 = a01 + a1Z1 + a2Z2 , |
(38) |
де a01 = ln(a0 ) . |
|
Далі обчислюємо параметри регресії, визначаємо |
якість та адекватність |
моделі, визначаємо границі надійних інтервалів для параметрів і прогнозу
показника, |
як |
було |
вище |
зазначено |
для множинної лінійної .моделіДля |
параметра |
a01 |
та |
границь |
надійного |
інтервалу прогнозу показника треба |
зробити зворотні перетворення: знайти за допомогою потенціювання.
Приклад розрахунку виробничої функції – на стор. 36-37. 34
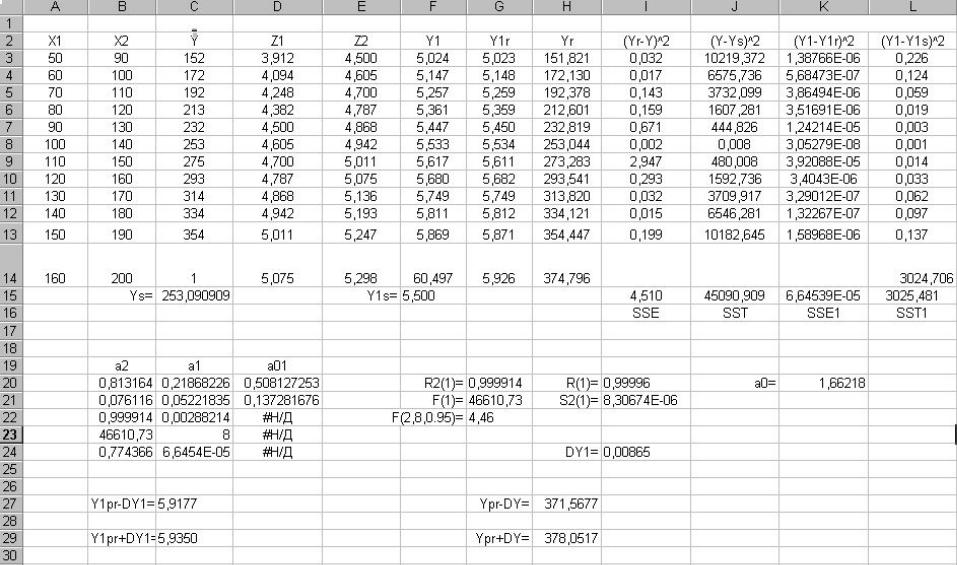
35
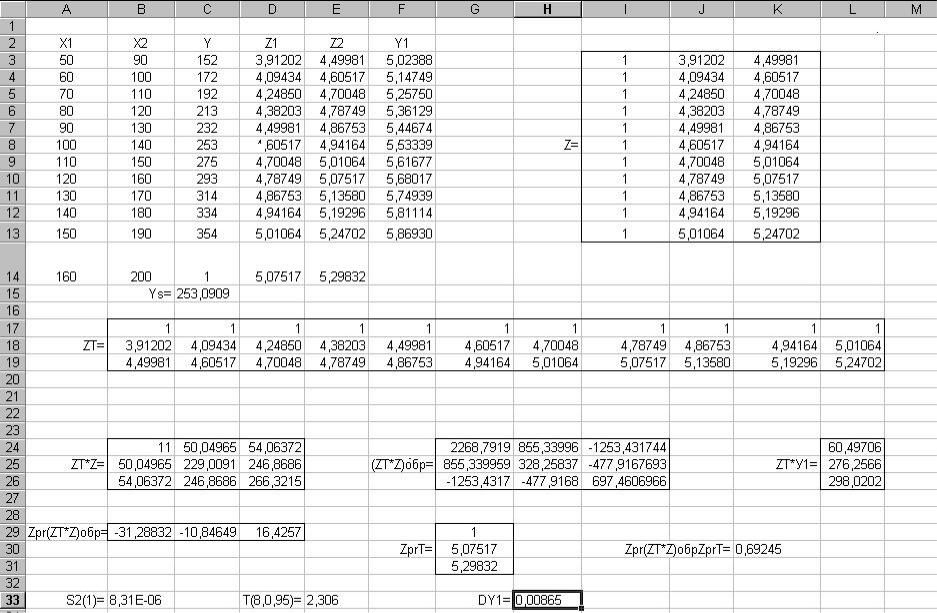
Завдання для самостійного виконання
Значення ціни, попиту та пропозиції на певний вид товару наведені в
таблиці:
Ціна |
Попит |
Пропозиція |
Х |
У1 |
У2 |
1 |
8.41 |
1.70 |
2 |
7.38 |
2.01 |
3 |
6.43 |
2.54 |
4 |
6.48 |
3.38 |
5 |
5.62 |
3.87 |
6 |
4.75 |
4.77 |
7 |
3.88 |
5.65 |
8 |
3.31 |
6.35 |
9 |
2.67 |
6.48 |
10 |
2.18 |
7.31 |
11 |
1.60 |
8.41 |
На основі статистичних даних оцінити параметри регресії попиту та пропозиції, якщо припустити, що стохастичні залежності між попитом і ціною та пропозицією і ціною мають такий вигляд:
Y1 = a0 + a1 X1 + a2 X 2 + e1 ,
Y2 = b0 + b1 X1 + b2 X 2 + e2 .
Використовуючи критерій Фішера, з надійністю =0Р.95 оцінити адекватність економетричних моделей статистичним даним, статистичну значимість параметрів за критерієм Стьюдента.
Знайти графічно та аналітично точку ринкової рівноваги. Для рівноважної ціни визначити границі довірчого інтервалу.
Питання для самоконтролю
1.Які перетворення змінних проводяться у випадку квазілінійної парної регресії для різних функцій?
2.Наведіть приклади нелінійної регресії відносно параметрів та змінних.
37
3.Які перетворення змінних у випадку нелінійної відносно змінних та параметрів парної регресії необхідно провести для зведення регресії до лінійної?
4.Як перетворюються змінні у випадку квазілінійної множинної регресії ?
5.Наведіть приклади нелінійної регресії відносно параметрів та змінних.
6.Які перетворення змінних проводяться у випадку нелінійної відносно змінних та параметрів багатофакторної регресії?
7.Які особливості визначення меж довірчого інтервалу прогнозу у випадках різних типів нелінійностей?
Література
[1-9]
38