Математичні моделі у фінансах / Рядно О.А. та ін. Математичні моделі у фінансах

РОЗДІЛ 3 ІМОВІРНІСНІ МОДЕЛІ У ФІНАНСАХ

3.1. Система кількісних оцінок ступеня ризику

Мета вивчення теми – набуття студентами навичок застосування імовірнісних моделей у фінансах при прийнятті управлінських рішень.

Вивчення теми базується на знаннях, отриманих студентами з дисципліни „Теорія імовірностей і математична статистика”.

Детально аналіз фінансової діяльності підприємства та управління запасами з урахуванням ризику розглянуто у посібнику [5] (відповідно розділи 3, 5). У роботі [1] докладно розглянуто модель оцінювання ринкової вартості підприємства (розділ 4, п. 4.3), модель вибору інвестиційного проекту з множини альтернативних варіантів (розділ 4, п. 4.4), а також мікроекономічне моделювання банківської діяльності (розділ 10).

Ризик – категорія імовірнісна, тому його вимірювання базується на теоретико-ймовірнісному підході, основними поняттями якого є випадкова величина та закон розподілу. Серед випадкових величин розрізняють дискретні та неперервні величини. В економіці, як правило, оперують дискретними випадковими величинами. Надалі замість терміна «дискретна випадкова величина» будемо вживати термін «випадкова величина». Закони розподілу випадкової величини можна задати таблицями, аналітично та графічно. При табличному способі завдання розподілу дискретної випадкової величини перший рядок таблиці містить усі можливі значення випадкової величини, а друга – їх ймовірності:

При аналізі ризику розрізняють економічні показники з позитивним та негативним інгредієнтом. Вважають, що економічний показник має позитивний інгредієнт, якщо при прийнятті рішення орієнтуються на його максимальне значення. Для цих випадків

записують, що X X . Якщо ж під час прийняття рішень орієнтуються на мінімальне значення економічного показника, то вважають, що він має негативний інгредієнт. У цій ситуації пишуть, що X X .

Нехай випадкову величину X задано таблицею. Розглянемо кількісні оцінки ступеня ризику, що найбільш часто застосовуються в аналізі ризику:

61

Ризик як величина очікуваної невдачі (сподіване значення,

математичне сподівання):

j 1

Ризик як ступінь мінливості результату. В якості величини ризику в абсолютному вираженні часто використовується ступінь розсіювання значень економічного показника відносно центра групування цих значень, зокрема використовується дисперсійний підхід. Дисперсією (варіацією) V(X) випадкової величини X є зважена щодо ймовірності величина квадратів відхилення випадкової величини X від її математичного сподівання M(X):

j 1

Середньоквадратичним (стандартним) відхиленням випадкової величини X називається величина:

Підхід до оцінки ризику, що спирається на варіацію чи середньоквадратичне відхилення, вважається класичним. Причому чим більшими будуть ці величини, тим більшим буде ступінь ризику, пов’язаного з певною стратегією, тобто величина ризику:

Слід зазначити, що такий підхід до оцінки ступеня ризику використовується для показника X як з позитивним, так і негативним інгредієнтом.

Треба мати на увазі, що при класичному визначенні ступеня ризику однаково трактуються як додатні, так і від’ємні відхилення величини реального ефекту від сподіваної величини, тобто виконується гіпотеза про те, що коливання випадкової величини X (прибутку, чистої приведеної вартості, збитків) в обидві сторони однаково небажані.

За неокласичною теорією економічного ризику, ризик пов'язаний лише з несприятливими для менеджера (інвестора) ефектами, тому для його оцінювання достатньо брати до уваги лише

62

несприятливі відхилення від сподіваної величини. При цьому в якості ступені ризику використовується семіваріація, яка обчислюється за формулою:

j 1

індикатор несприятливих відхилень, який визначається за формулою:

З практичної точки зору, більш зручніше (беручи до уваги вимірність величин) застосовувати семіквадратичне відхилення

SSV(X):

Ризик у відносному вираженні. Коефіцієнт сподіваних збитків Kz враховує обсяг сподіваних збитків по відношенню до суми абсолютних значень сподіваних вигод та сподіваних збитків. Він обчислюється за формулою:

63

де Mz , Mz – це умовні математичні сподівання щодо відхилень, які обчислюються за формулами:

j – індикатор несприятливого (по відношенню до Z )

відхилення, j – індикатор сприятливого (по відношенню до Z )

відхилення.

Наприклад, коли випадкова величина X має позитивний інгредієнт, то:

У випадку, коли оцінюється ризик як варіабельність щодо отримання доходів, то для оцінки ризику використовується коефіцієнт варіації, тобто відношення середньоквадратичного відхилення економічного показника ефективності X з позитивним інгредієнтом до сподіваного значення цього показника:

Коефіцієнту варіації можна надати таке економічне трактування: це величина ризику, що припадає на одиницю доходу. Коефіцієнт варіації має негативний інгредієнт, тобто чим менше для

проекту значення CV(X ), тим меншим відносним ризиком він обтяжений. Якщо відповідь щодо оптимального рішення, за допомогою виходячи з коефіцієнта варіації, дати неможливо, можна скористатися критерієм мінімального коефіцієнта семіваріації, який обчислюється за формулою:

64

Коефіцієнти асиметрії та ексцесу. У випадку асиметричного розподілу випадкової величини X аналіз лише середньоквадратичного відхилення як міри ризику може бути недостатнім. У цьому випадку слід аналізувати як показник ризику таку числову характеристику випадкової величини, як коефіцієнт асиметрії As(X), який обчислюють за формулою:

випадку, коли показники ефективності об’єкта мають негативний інгредієнт, тобто X X (сподівані збитки, затрати), більш ефективним рішенням будуть відповідати менші значення коефіцієнта асиметрії.

У ситуації, коли аналіз певних показників ефективності об’єкта показує, що ці показники мають майже однакові сподівані значення, приблизно рівні їхні середньоквадратичні відхилення і семіквадратичні відхилення, а також є рівними значення коефіцієнтів асиметрії, то для порівняння ризиковості цих проектів можна скористатися коефіцієнтом ексцесу Ex(X), який обчислюється за формулою:

Серед альтернативних об’єктів найменш ризиковий той, для якого «концентрація» значень показника ефективності в колі його сподіваного значення є вищою, тобто для якого значення коефіцієнту ексцесу максимальне.

На практиці за наявності статистичної інформації щодо спостережених значень xj ( j 1,n, n – кількість спостережень)

показника X можна використовувати статистичні оцінки показників ризику, що розглянуті вище:

65

Оцінка систематичного ризику. В аналізі ризику відрізняють ризик, який не можна усунути жодними методами, оскільки він присутній систематично і зумовлений зовнішніми факторами, і ризик, що залежить від діяльності конкретного підприємства чи галузі. Систематичний ризик оцінюється коефіцієнтом чутливості , що визначає рівень коливань у результатах діяльності галузі стосовно результатів діяльності ринку чи всієї економіки. З практичною метоюзручно обчислювати за такою формулою:

j 1

де yj – спостережені значення показника Y , що характеризує відповідні результати діяльності ринку чи всієї економіки.

66

Коефіцієнт показує рівень коливань чи відхилень у результаті діяльності підприємства або галузі, що розглядаються, які описуються показником X стосовно результатів діяльності ринку чи всієї економіки. За допомогою цього коефіцієнта можна зіставити діяльність підприємства чи галузі з усім ринком: галузь з показником1 має коливання результатів, що на рівні ринкових, з 1 – менші від ринкових, з 1 – вищі від ринкових.

При дослідженні економічного ризику за допомогою електронних таблиць Excel можна використовувати такі вбудовані функції:

Математичні функції:

«КОРЕНЬ» – знаходить корінь квадратний із числа; «СТЕПЕНЬ» – підносить число до заданого степеню; «СУММ» – знаходить суму всіх чисел вказаного масиву; «СУММКВ» – знаходить суму квадратів усіх чисел вказаного

масиву;

Статистичні функції:

«ДИСПР» – знаходить зміщену оцінку дисперсії генеральної сукупності;

«КВАДРОТКЛ» – знаходить суму квадратів відхилень величин від їх середнього значення;

«КОВАР» – знаходить оцінку статистичного кореляційного моменту між двома масивами однакової розмірності;

«КОРРЕЛ» – знаходить коефіцієнт кореляції між двома масивами однакової розмірності;

«СРЗНАЧ» – знаходить середнє значення масиву даних; «СТАНДОТКЛОНП» – знаходить зміщену оцінку середньоква-

дратичного відхилення випадкової.

Використовуючи пакет “Анализ данных”, пункт меню “Гистограмма” в електронних таблицях Excel можна побудувати гістограму частот, яка являє собою фігуру, що складається з

прямокутників, кожен з яких має основу h і висоту ni 1 (h xi xi 1 – h

довжина часткового і-го інтервалу можливих значень випадкової величини Х, ni частота появи значення Х в частковому і-ому інтервалі). Для цього необхідно задати вхідний інтервал (виділити значення показника Х, для якого ми будуємо гістограму) та інтервал карманів (задати часткові інтервали, в межі яких можуть потрапляти значення показника Х), а також відзначити у діалоговому вікні вивід графіку. Гістограма частот наочно показує про статистичний закон розподілу випадкової величини Х, яку ми досліджуємо.

67

3.2. Ризик діяльності малих підприємств регіону

Вихідні дані та результати розрахунків. Мале підприємництво – невід’ємна складова будь-якої ринкової господарської системи, основа її інноваційного розвитку, оскільки це найбільш динамічна, гнучка форма ділового життя. У той же час, діяльність малих підприємств характеризується підвищеним ризиком. На рис. 3.1 показано динаміку рентабельності операційної діяльності малих підприємств та підприємств-суб’єктів підприємницької діяльності Дніпропетровської області у 2002-2005 рр.

Рис. 3.1 Рентабельність операційної діяльності підприємств Дніпропетровської області у 2002-2005 рр.

Як бачимо з рис. 3.1, протягом періоду, що розглядався, рентабельність операційної діяльності малих підприємств Дніпропетровської області була суттєво нижчою за рентабельність діяльності усіх підприємств-суб’єктів підприємницької діяльності та не перевищувала 2% – це дуже низький показник.

Проаналізуємо більш детально ризик діяльності малих підприємств Дніпропетровської області. На листі “вихідні дані” файла priklad1.xls електронного додатка наведено дані по рентабельності операційної діяльності малих підприємств за регіонами Дніпропетровської області у 2004-2005 рр. Дані наведено як загалом, так і за окремими видами економічної діяльності. Для порівняння наведено дані по рентабельності операційної діяльності підприємствсуб’єктів підприємницької діяльності у відповідний період за регіонами області. На цьому ж листі наведено результати попередніх розрахунків, зокрема, розрахунків математичного сподівання M(X), дисперсії V(X), середньоквадратичного відхилення (X) та коефіцієнта варіації CV(X) показників, що розглядаються. При аналізі рівня рентабельності ми орієнтуємось на його максимальні значення, тобто показник, що аналізується, має позитивний

68

інгредієнт: X X . Дослідження показує, що майже для всіх видів економічної діяльності малих підприємств математичне сподівання є від’ємною величиною, що свідчить про незадовільний стан фінансової діяльності цих підприємств. Були також розраховані показники систематичного ризику діяльності малих підприємств відносно діяльності усіх підприємств-суб’єктів підприємницької діяльності. У 2004 та 2005 рр. отримано відповідно такі значення коефіцієнта чутливості: 0,58 та 0,47. Як бачимо, за два роки значення коефіцієнта було меншим за одиницю. Це свідчить про те, що ризик діяльності малих підприємств Дніпропетровської області багато в чому зумовлений загальним станом її економіки.

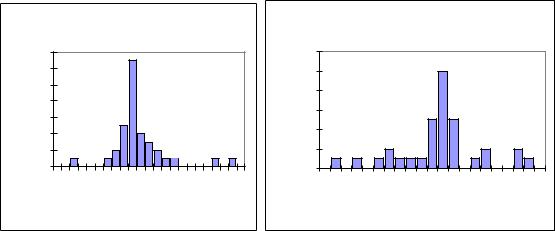
На листах “розрахунок 1” і “розрахунок 2” наведено результати розрахунку показників ризику операційної діяльності малих будівельних підприємств відповідно у 2004 та 2005 рр. Спочатку проаналізуємо гістограми частот, які наведено на рис. 3.2. Як бачимо з рис. 3.2, на обох гістограмах розподіл нагадує нормальний, у той же час розподіл частот у 2004 р. був трохи зміщений праворуч, а у 2005 р. – вже ліворуч.

Рис.3.2 – Гістограми частот рівня рентабельності операційної діяльності малих будівельних підприємств

У табл. 3.1 наведено кількісні оцінки ризику операційної діяльності малих будівельних підприємств Дніпропетровської області, що були отримані в результаті розрахунків. Аналіз табл. 3.1 свідчить про те, що майже усі показники ризику діяльності малих будівельних підприємств у 2005 р. погіршились: математичне сподівання рівня рентабельності M(X) зменшилось з 6% майже до 0, у той же час

трохи зменшилась дисперсія V(X) та середньоквадратичне відхилення (X), але значення коефіцієнта варіації CV(X), яке у 2005 р. підвищилось більш ніж у 10 разів, свідчить про суттєве підвищення у даному році ризику діяльності малих будівельних підприємств.

69

Коефіцієнт асиметрії у 2005 р. став від’ємним (це відповідає нашому попередньому аналізу гістограм), тобто якщо у 2004 р. несприятливі відхилення від сподіваного значення з відносно великою ймовірністю розташовувались ліворуч найближче до сподіваного значення, а сприятливі значення були значно віддалені від сподіваної величини (ці значення – “хвіст” – були розташовані праворуч), то у 2005 р. вже навпаки, несприятливі значення ліворуч були значно віддалені від сподіваної величини. Відповідно у 2005 р. збільшились семіваріація, семіквадратичне відхилення та коефіцієнт семіваріації, які характеризують розкид несприятливих значень показника.

Таблиця 3.1

Кількісні оцінки ризику операційної діяльності будівельних малих підприємств Дніпропетровської області

У 2005 р. зменшився коефіцієнт ексцесу, тобто крива розподілу стала більш пологою, більш “згладженою”. Ця ситуація вказує на те, що розміри інтервалу, на який “найчастіше” потрапляють значення показника ефективності, зріс, тобто ризикованість діяльності підприємств за цим показником у 2005 р. також зросла. Негативним явищем є збільшення у 2005 р. коефіцієнта сподіваних збитків, який у 2004 р. був меншим за 0,5, у 2005 – вже більшим.

Завдання до самостійної роботи

Використовуючи дані, наведені на листі “Вихідні дані” файла priklad1.xls, побудуйте гістограми частот для показників рентабельності малих підприємств та підприємств суб’єктів підприємницької діяльності Дніпропетровської області. Проаналізуйте їх та зробіть порівняльний аналіз;

70