Математичні моделі у фінансах / Рядно О.А. та ін. Математичні моделі у фінансах

У табл. 4.7 наведено деякі показники соціально-економічного розвитку України у 2000-2005 рр.

Таблиця 4.7

Порівняльна характеристика показників соціально-економічного розвитку України у 2000-2005 рр.

Назва показника 2000 р. 2001 р. 2002 р. 2003 р. 2004 р.2005р.

Як бачимо з табл. 4.7 протягом періоду, що розглядався, показники зайнятості в країні суттєво покращились. Розмір середньодушової ВДВ збільшився майже в три рази. Також збільшилась кількість підприємств суб’єктів підприємницької діяльності та як наслідок підвищився рівень зайнятості. Середньомісячна номінальна заробітна плата зросла за цей період більш ніж у три рази, чим можна пояснити покращання економічного положення в країні.

Розглянемо більш детально показники зайнятості та оплати праці на підприємствах – суб’єктах підприємницької діяльності за основними видами економічної діяльності. Значення даних показників, а саме середньорічної кількості найманих працівників, середньої кількості найманих працівників на одному підприємстві та середньомісячної заробітної плати по Україні наведено у табл. 4.7.

Аналіз табл. 4.7 показує, що у 2005 р. порівняно з 2000 р. середньорічна кількість найманих працівників в Україні зменшилась майже за всіма видами економічної діяльності. У той же час необхідно зазначити, що змінювалась вона нерівномірно. Ринкові реформи, зазвичай, супроводжуються глибокою структурною перебудовою, що призводе до перерозподілу ресурсів та концентрації їх на розвитку перспективних галузей, і відповідно до згортання таких галузей, продукція яких не рентабельна.

121

Таблиця 4.8

Показники зайнятості та оплати праці на підприємствах - суб’єктах підприємницької діяльності України за основними видами економічної діяльності

На рис. 4.16 наведено індекс середньорічної кількості найманих працівників у 2005 р. по відношенню до 2000 р. (Y).

Рис. 4.16. Середньорічна кількість найманих працівників підприємств – суб’єктів підприємницької діяльності України за 2005 р. у відсотках до

2000 р.

122

Як можна бачити з рис. 4.16, середньорічна кількість працівників найбільш суттєво зменшилась у сільському господарстві, а за такими видами економічної діяльності як виробництво та розподіл електроенергії, газу та води, операції з нерухомістю, здавання під найм та послуги юридичним особам, освіта, охорона здоров’я та соціальна допомога, колективні, громадські та особисті послуги середньорічна кількість найманих працівників збільшилась.

Середня кількість найманих працівників на 1 підприємстві у період, що розглядався, також зменшилась майже за всіма видами економічної діяльності (за винятком освіти), причому дуже суттєво (див. табл. 4.8).

Розподіл індексу середньомісячної заробітної плати у 2005 р. відносно до 2000 р. (X) за видами економічної діяльності показано на рис. 4.17.

Рис. 4.17. Середньомісячназаробітна плата на підприємствах– суб’єктах підприємницької діяльності України за 2005 р. у відсотках до 2000 р.

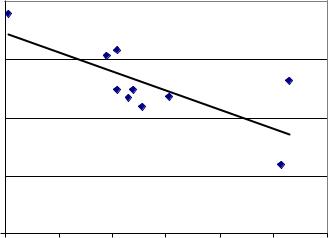
Як можна бачити з рис. 4.17 найбільш суттєво заробітна плата зросла у сільському господарстві, колективних, громадських і особистих послугах і в будівництві. Аналізуючи рис. 4.16, 4.17 можна побачити, що спостерігається статистичний зв’язок між динамікою середньорічної кількості найманих працівників і динамікою середньомісячної заробітної плати. Для виявлення цього зв’язку було побудовано рівняння лінійної регресії індексу кількості працівників (Y) від індексу зарплати (X). За методом найменших квадратів оцінено таку модель:

(4,94) ( 3,07)

де R2 – значення коефіцієнта детермінації. У дужках наведено розрахункові значення t – статистики. Як можна бачити, усі отримані оцінки параметрів значимі на рівні 5%. Статистичну залежність індексу кількості найманих працівників від індексу номінальної заробітної плати та лінію регресії, що побудовано, показано на рис. 4.18.

123

Рис. 4.18 Залежність індексу кількості найманих працівників на підприємствах – суб’єктах підприємницької діяльності України (Y)

від індексу середньомісячної заробітної плати (X)

Таким чином, модель, що побудована, дозволяє зробити висновок про те, що динаміка кількості працівників на підприємствах України обумовлена динамікою середньомісячної зарплати: збільшення індексу заробітної плати на 1% за інших рівних умов призводе до зменшення індексу кількості працівників на 0,5%.

Можна сказати, що отримане рівняння регресії встановлює наявність від’ємної лінійної статистичної залежності між динамікою попиту на працю і динамікою номінальної заробітної плати в Україні.

Було розглянуто середні за 3 роки (2003-2005 рр.) значення індексу кількості найманих працівників (YU ) і середньомісячної заробітної плати ( XU ) у відсотках до попереднього року для України. За методом найменших квадратів отримано таке рівняння регресії:

Як можна бачити, існує лінійна від’ємна статистична залежність щорічної динаміки кількості найманих працівників країни від щорічної динаміки середньомісячної заробітної плати, тобто існує від’ємна залежність між щорічною динамікою попиту на працю і заробітною платою в Україні. Причому побудована модель лише на 28% пояснює щорічні зміни кількості найманих працівників, решта 72% зумовлена чинниками, що лежать поза межами моделі.

124

Таблиця 4.9

Порівняльна характеристика структури середньорічної кількості найманих працівників в Україні у відсотках

Вид економічної діяльності 2002 р. 2003 р. 2004 р. 2005 р.

Трансформаційні процеси, що відбуваються зараз в Україні, визначають зміну структури зайнятих як в країні, так і в регіоні. У табл. 4.9 наведено порівняльну характеристику структури середньорічної кількості найманих працівників в Україні у 2000-2005 рр.

Як бачимо з табл. 4.9, протягом періоду, що розглядався, збільшилась питома вага працівників, що зайняті у промисловості, в оптовій та роздрібній торгівлі та в операціях з нерухомістю. У той же час питома вага зайнятих у сільському господарстві суттєво зменшилась на 6,5%. Найбільша частка найманих працівників у промисловості і становить 41,8% від загальної кількості найманих працівників на підприємствах країни. Найменша ж частка найманих працівників припадає на галузі освіти та охорони здоров’я і становить 0,8% та 0,9% відповідно.

Висновки. Таким чином, дослідження стану ринку праці, проведене на основі даних Державного комітету статистики, показало, що динаміка кількості працівників на підприємствах України обумовлена динамікою середньомісячної зарплати: збільшення індексу заробітної плати за інших рівних умов призводе до зменшення індексу кількості працівників.

125

Завдання до самостійної роботи

Використовуючи дані, що наведені на листі «Вихідні дані» файла pryklad 4.7.xls середньорічної кількості найманих працівників, середньомісячної заробітної плати та середньої кількості найманих працівників по Україні та Дніпропетровській області, побудуйте моделі, що пояснюють стан ринку праці Дніпропетровської області, як промисловорозвинутого регіону. Проаналізуйте їх та зробіть висновки. Зробіть порівняльний аналіз структури ринку праці країни та Дніпропетровської області.

Використовуючи статистичні дані Головного управління статистики у Дніпропетровській області [36-40], знайдіть значення інших показників, що характеризують ринок праці. Проаналізуйте результати, зробіть порівняльний аналіз.

Питання до самоконтролю

1.Наведіть приклади застосування моделей регресії в аналізі фінансової діяльності підприємств.

2.Наведіть приклади застосування регресійних моделей у моделюванні бюджетних процесів.

3.У чому полягає економічна сутність кривої Лаффера?

4.Запишіть та проаналізуйте криву Лаффера у випадку степеневого закону згасання економічної активності.

5.Запишіть та проаналізуйте криву Лаффера у випадку експоненціального закону згасання економічної активності.

6.Опишіть основні підходи до визначення сукупної податкової ставки податку.

7.Критерій оптимальності податкової системи в моделі кривої Лаффера.

8.Наведіть приклади застосування фіктивних змінних при аналізі бюджетних процесів.

9.Наведіть приклади застосування регресійних моделей у дослідженні проблем соціального страхування.

Рекомендована література: [17], [26].

126

РОЗДІЛ 5 СУЧАСНІ ЕКОНОМЕТРИЧНІ МОДЕЛІ У ФІНАНСАХ

5.1. Моделі панельних даних

Мета вивчення теми – набуття студентами навичок застосування сучасних економетричних моделей у дослідженнях проблем фінансів при прийнятті управлінських рішень.

У даній темі розглядається застосування у дослідженнях проблем фінансів таких сучасних економетричних методів, як ARIMA–моделі і моделі панельних (лонгітюдних) даних.

Моделі ARIMA застосовуються в економічному прогнозуванні. Застосування ARIMA–моделей для прогнозування податкових надходжень розглянуто у посібнику [1] (розділ 4, п. 4.5). Докладно методику побудови ARIMA–моделей наведено у посібнику [18]. Треба зауважити, що ARIMA–аналіз є порівняно новим поколінням засобів прогнозування, заснованих на аналізі імовірнісних (стохастичних) властивостей часових рядів. При цьому відповідний часовий ряд yt моделюється лише за допомогою минулих значень (лагів) та екзогенної випадкової величини. Моделі ARIMA часто називають атеоретичними моделями, оскільки в переважній більшості випадків моделювання не вимагає економіко-теоретичного підґрунтя специфікації моделі. Необхідною умовою застосування ARIMA– методології є стаціонарність часового ряду, який розглядається. Якщо він є стаціонарним, то його можна змоделювати різними способами, зокрема за допомогою двох складових – авторегресійної (AR) та ковзкого середнього (MA). Відповідно сама модель ARMA є комбінацією цих двох складових:

параметр, що визначає середнє значення; T – кількість періодів спостережень; t – “білий шум”.

На жаль, у більшості часових рядів економічних показників випадки існування стаціонарних випадкових процесів трапляються рідко. Для приведення процесу до стаціонарного виду, як правило, використовується оператор різниці, і, відповідно, модель ARMA перетворюється в модель ARIMA.

127

Порядок моделі ARIMA задається трьома параметрами: порядок авторегресії p; порядок оператора різниці d для приведення процесу до стаціонарного вигляду; порядок моделі ковзного середнього q.

Моделі панельних даних детально розглянуто у навчальному посібнику [18] (розділ 5). Панельні дані є спостереженнями за одними й тими самими економічними одиницями або об’єктами (за індивідуумами, домашніми господарствами, фірмами, регіонами, країнами і т.ін.), які здійснюються в послідовні проміжки часу. Прикладом можуть бути щорічні бюджетні обстеження одних і тих самих домашніх господарств, щоквартальні данні про діяльність фіксованої множини підприємств, щорічні показники певної групи країн. Таким чином, панельні дані поєднують дані просторового типу

(cross-sectional data) і дані типу часових рядів (time-series data): у

кожний момент часу є дані просторового типу по економічним одиницям, і для кожного такого об’єкту відповідні йому дані утворюють один або декілька часових рядів. Завдяки спеціальній структурі панельні дані дозволяють будувати більш глибокі та змістовні моделі та отримувати відповіді на питання, які недоступні у рамках, наприклад, моделей, що базуються тільки на даних спостережень за об’єктом у фіксований момент часу. Зокрема, виникає змога враховувати та аналізувати індивідуальні відмінності між економічними одиницями, що неможливо зробити в рамках стандартних регресійних моделей.

Зазначимо, що для моделювання регіональних соціальноекономічних процесів зручно використовувати саме апарат панельних даних. Тому останнім часом все поширенішим стає групування часових рядів однакових показників для певних регіонів та їх одночасний аналіз.

У загальному вигляді модель панельних даних може бути представлена так:

де yit – значення залежної змінної для і-го об’єкта у t-й період часу,

та j – невідомі параметри моделі, xjit – значення j-го фактора для і-го об’єкта у t-період часу, it – значення випадкової величини;

Модель типу (5.2) фактично є регресійною моделлю на множині панельних даних. Побудова, оцінювання параметрів та дослідження такої моделі нічим не відрізняється від класичних багатофакторних регресійних моделей.

Специфіка моделей панельних даних надає можливість додатково розбивати збурення на декілька компонентів. Найбільш поширеними на практиці є моделі, в яких ми можемо виділити один окремий компонент збурення моделі (5.2):

128

де є спільним перетином. Отже, в моделі з випадковими ефектами, на відміну від моделей з фіксованими, можна виділити та окремо оцінити спільний перетин.

Розглянемо більш детально модель панельних даних з фіксованими ефектами (5.4).

Як легко побачити, модель (5.4) є фактично лінійною регресійною моделлю, в якій перетини варіюються залежно від об’єкта і. Тому її можна переписати у вигляді звичайної лінійної регресійної моделі, включивши фіктивну змінну для кожного об’єкта і:

чином, ми маємо додатково n фіктивних змінних у моделі (5.4). Звичайно, на практиці незручно оцінювати регресійну модель з

великою кількістю додаткових фіктивних змінних, особливо коли n достатньо велике, через те, що ми втрачаємо ступені свободи. На щастя, ми можемо оцінити невідомі параметри моделі (5.4) у дуже простий спосіб. Можна показати, що ті ж самі оцінки параметрів можна отримати з регресійної моделі, де фактори

подаються у формі відхилень від середнього окремого регіону. Фактично це означає, що ми виключаємо індивідуальні ефекти з моделі за допомогою трансформації даних, а потім оцінюємо їх після оцінки параметрів a1, a2,...,am.

Розглянемо дану трансформацію детальніше. Зауважимо, що з моделі (5.4) легко отримати модель вигляду:

Віднявши від обох частин моделі (5.4) відповідні частини моделі (5.7), отримаємо модель зі змінними у відхиленнях від середнього:

Модель (5.9) є трансформованою моделлю, яка не включає індивідуальні ефекти i. Така трансформація називається трансформацією у крос-секційному розрізі. Відповідно оцінки

130