
Математичні моделі у фінансах / Рядно О.А. та ін. Математичні моделі у фінансах
.pdf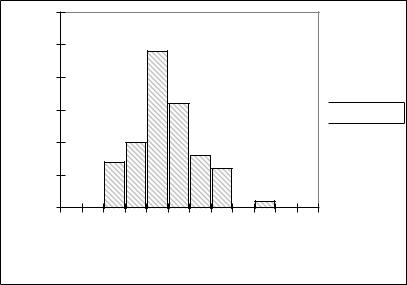
автокореляції для 1% рівня значимості), можемо зробити припущення про нормальний закон розподілу залишків даної моделі.
Частота
30 |
|
|
|
|
25 |
|
|
|
|
20 |
|
|
|
|
15 |
|
|
|
|
10 |
|
|
|
|
5 |
|
|
|
|
0 |
|
|
|
|
10 |
5 |
0 |
5 |
10 |
- |
|
|
||
- |
|
|
|
|

 Частота
Частота
L
Рис. 5.6. Гістограма частот залишків L прогнозної моделі податку з доходів фізичних осіб у порівняльних цінах
За допомогою моделі, що побудовано, отримано прогнозні значення надходжень від податку з доходів фізичних осіб на 2006 р.
Визначимо як одну з компонент вектора податкового ризику ймовірність можливого недовиконання планових податкових надходжень [1]. Ризик 10%-го недовиконання планового показника за прогнозування на один крок дорівнюватиме:
|
|
|
|
|
0,1 |
|
|
|
|
|
P(Y |
0,9Yˆp ) 1 Ф |
|
|
|
, |
(5.12) |
||
|
V |
||||||||
|
|
|
|
|
|
|
|
||
де |
V – аналог коефіцієнта варіації: |
|
|
|
|
|
|||
|
|
V |
s |
, |
|
|
|
|
(5.13) |
|
|
|
|
|
|
|
|||
|
|
|
Yˆp |
|
|
|
|
Yˆp – |
|
|
s – похибка прогнозу, отримана на базовому інтервалі; |
||||||||
прогнозоване значення податкових надходжень; Ф(Y) – функція Лапласа.
В електронних таблицях Excel функція Лапласа розраховується за допомогою статистичної функції НОРМРАСП (Y , 0, 1, 1).
Так згідно з отриманим прогнозом, у січні 2006 р. очікувались надходження від податку з доходів фізичних осіб в обсязі 141,6 млн. грн.,
141

похибка прогнозу s=6,38 млн.грн., V=0,045. Величина ступеня ризику як ймовірність недоотримання податкових надходжень від податку з доходів фізичних осіб по Дніпропетровській області становила:
|
0,1 |
|
|
|
P(Y 0,9Yˆp) 1 Ф |
|
|
|
1 Ф(2,219) 0,013. |
|
|
|||
0,045 |
|
|
||
Тобто ймовірність 10%-го недовиконання планового показника податку з фізичних осіб складає 0,013, або 1,3%.
За збільшенням прогнозованого інтервалу похибка прогнозу також збільшується. На річному інтервалі похибка розраховується за
її максимально можливим значенням s2(1 2 3 ... 12).
Таким чином, ми отримали прогноз надходжень до бюджету податку з доходів фізичних осіб у цінах грудня 2005 р. У той же час, у бюджетному процесі важливим є прогнозування податкових надходжень у номінальних цінах. Тому розглянемо тепер прогнозування обсягів податку з доходів фізичних осіб у фактичних цінах.
Побудуємо модель для прогнозу податку з доходів фізичних осіб Y у номінальних цінах. Результати розрахунків прогнозу показника Y , що не скорегований на індекс інфляції, наведено на листі “розрахунок2” файлу priklad8.xls.
Спочатку побудуємо модель регресії показника Y виду (5.11). Отримані у цьому випадку за методом найменших квадратів з використанням функції „ЛИНЕЙН” оцінки параметрів моделі (5.11) наведено у табл. 5.4. Таким чином, побудовано таку модель:
yˆt 31,9 1,51t 88,9x1t 1,28t x1t 5,30x2t 7,23x3t |
(5.14) |
. |
|
8,68x4t 18,7x5t |
|
Як бачимо з табл. 5.4, усі оцінки параметрів моделі можна вважати значимими на 1% рівні. Значення коефіцієнта детермінації
R2=0,97 наближується до 1. Відносна похибка регресії за формулою (4.11), що відображає прогнозні властивості моделі, складає:
s100% 6,5%. y
Аналіз залишків моделі L на основі побудованої гістограми (рис. 5.7) та дослідження наявності автокореляції за допомогою статистики Дарбіна-Уотсона (DW1=1,284<DWp=1,6<DW2=1,682 для 1% рівня значимості, конкретних висновків зробити не можемо) вже не дозволяє зробити висновок про їх нормальний розподіл. Крім
142
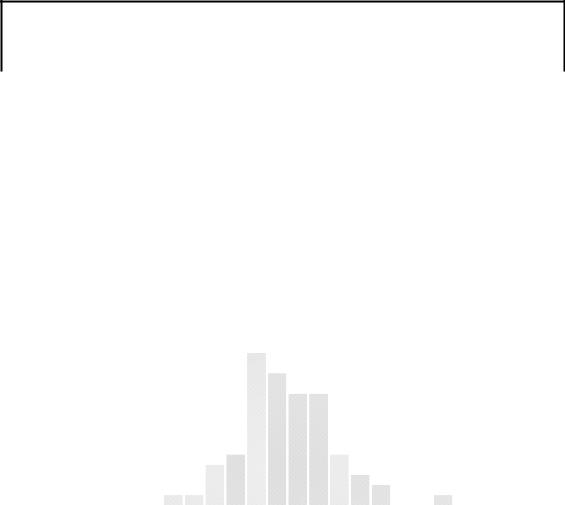
того, слід взяти до уваги, що зазвичай рівень цін є нестаціонарним рядом, а оскільки ціна входить складовою в показники у номінальному виразі, це збільшує порядок інтеграції часового ряду. Отже, ймовірно ми маємо справу з нестаціонарним часовим рядом.
Таблиця 5.4
Оцінки параметрів прогнозної моделі для податку з доходів фізичних осіб у фактичних цінах
Залежна змінна: Y
Незалежні |
Коефіцієнт |
|
|
Стандартна |
|
|
|
|
t - |
|
|
|
|
Р-рівень |
|||||||||||||||||
змінні |
|
|
|
|
|
|
|
|
|
|
похибка |
|
|
статистика |
значимості |
||||||||||||||||
Константа |
|
|
|
31,9 |
|
|
|
|
1,98 |
|
|
|
|
|
16,1 |
|
|
|
0,000 |
||||||||||||
T |
|
|
|
1,51 |
|
|
|
|
0,062 |
|
|
|
|
|
24,4 |
|
|
|
0,000 |
||||||||||||
X1 |
|
|
|
-88,9 |
|
|
|
10,9 |
|
|
|
|
|
-8,13 |
|
|
|
0,000 |
|||||||||||||
T X1 |
|
|
|
1,28 |
|
|
|
|
0,186 |
|
|
|
|
|
6,89 |
|
|
|
0,000 |
||||||||||||
X2 |
|
|
|
5,30 |
|
|
|
|
1,95 |
|
|
|
|
|
2,72 |
|
|
|
0,008 |
||||||||||||
X3 |
|
|
|
7,23 |
|
|
|
|
1,99 |
|
|
|
|
|
3,64 |
|
|
|
0,000 |
||||||||||||
X4 |
|
|
|
8,68 |
|
|
|
|
2,26 |
|
|
|
|
|
3,85 |
|
|
|
0,000 |
||||||||||||
X5 |
|
|
|
18,7 |
|
|
|
|
2,91 |
|
|
|
|
|
6,41 |
|
|
|
0,008 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частота |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
5 |
0 |
|
5 |
|
10 |
15 |
|
|
20 |
|
|
|
|
||||||||||||
|
|
15 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
- |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.7. Гістограма частот залишків L прогнозної моделі податку з доходів фізичних осіб у фактичних цінах
Для дослідження часового ряду на стаціонарність необхідно побудувати та проаналізувати автокореляційну та часткову автокореляційну функції, а також застосувати тест Дікі-Фуллера на наявність одиничного кореня. Виконати такі процедури дозволяють
143
сучасні статистичні пакети програм, зокрема, STATA, E.VIEWS, SPSS, STATISTICA.
Використовуючи можливості електронних таблиць Excel, змоделюємо залишки за допомогою ARIMA моделі. Ряд залишків позначимо YL. Результати побудови ARIMA моделі для ряду YL наведено на листі “розрахунок2”.
Будемо вважати, що порядок інтеграції ряду YL дорівнює 1, оскільки для економічних даних більш високі порядки інтеграції майже не зустрічаються. Створимо ряд перших різниць D1YL:
d1ylt ylt ylt 1, |
(5.15) |
та побудуємо модель для D1YL виду (5.1). Для цього необхідно вибрати специфікацію моделі, тобто визначити порядок p ARскладової моделі та порядок q MA-складової. Зауважимо, що не існує правила для знаходження ідеального порядку p і q. Один із найпростіших та найпоширеніших методів – аналіз корелограм. Його зручно застосовувати, використовуючи сучасні статистичні пакети програм. В електронних таблицях Excel будемо здійснювати вибір моделі на підставі зниження показника ризику, що визначається на основі значення абсолютної похибки регресії s та відносної похибки (4.11) [1]. Крім того, під час побудови моделі будемо враховувати похибки оцінок коефіцієнтів моделі (5.1) j, j, тобто модель
вважається адекватною, якщо всі її параметри будуть значимими на 5% рівні значимості. У результаті було вибрано модель вигляду:
d1ylt 0 1d1ylt 1 2d1ylt 2 t, |
(5.16) |
тобто p =2, q =0. Відзначимо, що аналіз корелограм за допомогою статистичного пакета програм STATA підтвердив обрану нами специфікацію моделі ARIMA(2,1,0) для ряду YL (моделі ARMA(2,0) для ряду D1YL).
Для побудови моделі (5.15) в електронних таблицях Excel було створено часові ряди D1YL_1 і D1YL_2, які отримано з ряду D1YL шляхом зсуву у часі відповідно на 1 і 2 періоди, та за допомогою функції „ЛИНЕЙН” знайдено оцінки параметрів моделі (5.16):
^ 0,141 0,588 d1yl |
0,441 a1yl |
. |
||
d1ylt |
t 1 |
t 2 |
(5.17) |
|
( 5,35) |
( 4,01) |
|||
|
|
|||
144
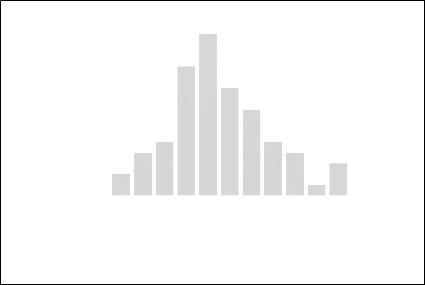
Оцінки параметрів даної моделі можна вважати значимими на 1% рівні. Аналіз залишків LL моделі (5.14) на основі побудованої гістограми (рис. 5.8) та статистики Дарбіна-Уотсона (DWp=2,00) дозволяє зробити припущення про їх нормальний розподіл.
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частота |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-10 |
5 |
0 |
5 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
-15 |
10 |
15 |
20 |
|
|
|||||||||||||||||
|
- |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
LL
Рис. 5.8. Гістограма частот залишків LL для моделі часового ряду YL
^
Для отримання прогнозу для ряду YL за допомогою побудованої моделі спочатку необхідно розрахувати за формулою
^
(5.17) прогнозні значення для ряду перших різниць D1YL, а потім від
^
прогнозних значень ряду перших різниць D1YL перейти до
^
прогнозних значень ряду YL:
^^
ylt ylt 1 |
d1ylt |
– для базового періоду; |
|
^ |
^ |
^ |
(5.18) |
|
|||
ylt |
ylt 1 d1ylt – для прогнозного періоду. |
||
Прогнозні значення надходжень від податку з доходів фізичних осіб Yˆp розраховуються як сума прогнозних значень показника Yˆ,
^
отриманих за формулою (5.14), та прогнозних значень ряду YL,
^^ ^
отриманих з рівняння (5.18): Y p Y YL.
145
Завдання до самостійної роботи
До розділу 5.2.
Використовуючи дані, наведені на листі “Вихідні дані” файла priklad7.xls, побудуйте модель панельної регресії з фіксованими ефектами, що встановлює залежність середньодушових обсягів доходів місцевих бюджетів dc від факторів zrp, prom, tvo, exp, imp. Проаналізуйте статистичну якість моделі та зробіть висновки;
візьміть дані за декілька років за регіонами Дніпропетровської області щодо середньодушових доходів місцевих бюджетів за окремими статтями надходжень і побудуйте моделі панельних регресій з фіксованими ефектами, що пояснюють ці надходження. Зробіть висновки.
До розділу 5.3.
використовуючи дані, що наведені на листі “Вихідні дані” файлу priklad8.xls, побудуйте моделі для прогнозування обсягів податкових надходжень від податку на прибуток підприємств, податку на додану вартість, акцизного збору, плати за землю, інших надходжень, а також загального обсягу податкових надходжень (у порівняльних цінах). Отримайте прогноз податкових надходжень на наступні два роки;
визначте ризик 10% недовиконання планового показника за прогнозування на один крок;
розрахуйте прогноз загального обсягу податкових надходжень як суму надходжень від окремих податків. Визначте ризик 10% недовиконання планового показника у цьому випадку. Порівняйте результати;
побудуйте моделі для прогнозування обсягів податкових надходжень з податку на прибуток підприємств, податку на додану вартість, акцизного збору, плати за землю, інших надходжень, а також загального обсягу податкових надходжень (у фактичних цінах). Отримайте прогноз податкових надходжень на наступні два роки.
Питання до самоконтролю
1. Наведіть приклади застосування моделей панельних даних на практиці. Які переваги мають моделі панельних даних порівняно з іншими моделями?
146
2.Наведіть основні проблеми, які можуть виникнути при застосуванні моделей панельних даних на практиці.
3.Запишіть модель панельних даних у загальному вигляді. Прокоментуйте та поясніть її.
4.Поясніть, у чому полягає основна відмінність між моделями панельних даних з фіксованими та випадковими ефектами.
5.У чому полягає особливість оцінювання невідомих параметрів моделей панельних даних з фіксованими ефектами?
6.Поясніть, коли ми повинні застосовувати моделі з фіксованими ефектами, а коли з випадковими. Яка принципова різниця між ними?
7.Поясніть, чому стаціонарність часових рядів є необхідною умовою розробки моделей авторегресії та ковзного середнього?
8.Опишіть загальну схему побудови ARMA-моделей.
9.Наведіть визначення нестаціонарного процесу та поясніть, що означає порядок інтеграції.
10.Запишіть та проінтерпретуйте модель ковзного середнього першого порядку МА(1). Прокоментуйте основні властивості МА(1)- процесу.
11.Прокоментуйте основні властивості ARMA(1,1)-процесу.
12.У чому полягає основна ідея прогнозу за ARIMA-моделями?
13.Чим відрізняються прогнози за AR(1) - та MA(1) - моделями?
14.Назвіть основні властивості прогнозів за AR(1) - моделями?
15.Поясніть сутність концептуальних засад, на які спирається проблематика прогнозування обсягів податкових надходжень з урахуванням ризику.
Рекомендована література: [1], [25], [26].
147
РОЗДІЛ 6 МЕТОДИ БАГАТОВИМІРНОГО СТАТИСТИЧНОГО АНАЛІЗУ
ФІНАНСОВОЇ ДІЯЛЬНОСТІ ПІДПРИЄМСТВ ТА РЕГІОНАЛЬНИХ І ДЕРЖАВНИХ ФІНАНСІВ
6.1. Рейтингове оцінювання та управління в економіці
Мета вивчення теми – набуття студентами навичок застосування методів багатовимірного статистичного аналізу й рейтингового управління фінансовою діяльністю підприємства та регіональними і державними фінансами у майбутній фаховій діяльності.
Рейтингове оцінювання та управління в економіці детально розглянуто у підручнику [1] (розділ 6).
У зв’язку зі складністю одночасного контролю великої кількості різноманітних показників у фінансово-економічному аналізі значного поширення набули методи зниження розмірності багатовимірних показників. Ці методи застосовуються, коли загальна кількість ознак, що реєструється на кожному з множини об’єктів (країн, регіонів, міст, підприємств, фірм, банків і т. ін.), дуже велика. При цьому кожне зі спостережень подається у вигляді деякого вектора допоміжних показників із суттєво меншою кількістю компонент. Нові допоміжні ознаки можуть вибиратись із числа вихідних або визначатися за якимось правилом за сукупністю вихідних ознак, наприклад як лінійні комбінації. При формуванні нової системи ознак до останніх пред’являються різного роду вимоги, такі як найбільша інформативність (у певному розумінні), взаємна некорельованість, найменше викривлення геометричної структури множини вихідних даних і т.ін. Залежно від варіанта формальної конкретизації цих вимог приходимо до того або іншого алгоритму зниження розмірності. Існує принаймні, три основні типи принципових передумов, що обумовлюють можливість переходу від більшого числа вихідних показників стану системи, що аналізується, до суттєво меншого числа найбільш інформативних змінних. Це, по-перше, дублювання інформації, що подається завдяки взаємопов’язаним ознакам; подруге, неінформативність ознак, що мало змінюються при переході від одного об’єкта до іншого (мала варіабельність ознак); по-третє, можливість агрегування, тобто простого або зваженого підсумовування , за деякими ознаками.
До методів зниження розмірності відносяться метод головних компонент, факторний аналіз, екстремальне групування параметрів і т. ін. Відзначимо, що метод головних компонент вже знайомий студентам з курсу економетрії. Детально він описаний у підручнику
[26].
На підставі процедур зниження розмірності і побудови узагальнених показників може обчислюватися рейтинг як узагальнена
148
оцінка діяльності економічної системи. Під рейтингом розуміють комплексну характеристику економічної системи згідно з певною шкалою, де значення рейтингу – це елемент лінійно напівупорядкованої множини.
Під рейтинговим управлінням розуміють концепцію прийняття рішень потенційними користувачами на підставі використання рейтингів у процесі реалізації функції управління. Із цього означення випливає, що рейтингове управління є процесом, у якому рейтинг використовується для аналізу, контролю, обліку, прогнозування та регулювання діяльності економічної системи. Тому методику обчислення рейтингу можна інтерпретувати як цільову функцію рейтингового управління, значення якої є індикатором економічної системи. Суттєвою характеристикою процесу рейтингового управління є те, що рейтингова оцінка одночасно виступає і як інструмент, і як мета управління. Вибір методики обчислення рейтингу залежить від конкретної стратегії управління. Остання визначається набором групи цілей, що відповідають різним аспектам функціонування економічної системи, які впорядковані за їх пріоритетами. Кожна ціль поділяється на елементарні складові, що впорядковуються як за пріоритетами, так і за термінами їх реалізації. З погляду рейтингового управління істотними є такі особливості рейтингового оцінювання:
-рейтинг є втіленням такої функції управління як аналіз у його чистому вигляді, тобто „аналіз високого рівня”;
-у підґрунтя рейтингової оцінки закладено принцип відповідності функціонування економічної системи низці критеріїв, тобто рейтинг є результатом процесу багатофакторного аналізу економічної системи.
6.2. Моделювання рейтингового оцінювання якості життя населення регіону
Вихідні дані та результати розрахунків. Моделювання рейтингового оцінювання якості життя населення має суттєве значення для оптимізації розподілу бюджетних коштів та контролю за ефективністю їх використання. Розглянемо на прикладі Дніпропетровської області моделювання рейтингу міст за якістю життя населення.
У файлі priklad9.xls електронного додатку на листі „Вихідні дані” наведено значення окремих показників соціально-економічного розвитку міст Дніпропетровської області за 2000-2003 рр., що розраховані на основі даних Головного управління статистики у Дніпропетровській області [36-40], які характеризують якість життя населення міст області за такими аспектами:
149
~ |
|
~ |
~ |
~ |
~ |
~ |
~ |
; |
– „Стан здоров’я” – X11, X12, |
X13, |
X14, |
X15 |
, X16 |
, X17 |
|||
~ |
~ |
~ |
~ |
~ |
|
|
|
|
– „Зайнятість” – X21, |
X |
22, X |
23, X |
24, X25; |
|
|
|
|
~~ ~ ~ ~
–„Умови праці” – X31, X32, X33, X34, X35;
~~
–„Злочинність” – X41, X42;
~~
–„Забезпеченість житлом” – X51, X52;
– |
~ |
~ |
, |
~ |
, |
~ |
, |
~ |
; |
„Особистий добробут” – X61, |
X62 |
X63 |
X64 |
X65 |
|||||
– |
„Заклади охорони здоров’я” – |
~ |
|
~ |
|
~ |
|
~ |
|
X71, |
X72, |
|
X73, |
|
X74; |
||||
– |
„Заклади культури та освіти” – |
~ |
|
~ |
|
~ |
, |
~ |
; |
X81, |
X82, |
X83 |
X84 |
||||||
– |
„Стан навколишнього середовища” – |
~ |
, |
~ |
, |
~ |
~ |
||
X91 |
X92 |
X93 |
, X94. |
||||||
Опис даних показників наведено у п.6.2.2.
На основі цих показників необхідно отримати рейтингову оцінку якості життя населення міст області.
У файлі priklad9.xls наведено приклад розрахунку узагальненого показника якості життя населення міст Дніпропетровської області за 2003 р. Для цього виконуються такі шаги:
Крок 1. Попередня уніфікація даних за формулами (6.1), (6.2) (див. п. 6.6.2). Результати розрахунків за першим кроком наведено на листі “розрахунок1” файла priklad9.xls.
Крок 2. Побудова інтегрального показника окремого аспекту якості життя населення. Результати розрахунків за другим кроком наведено на листі “розрахунок2” файла priklad9.xls. Тут наведено розрахунки інтегральних показників окремих аспектів якості життя населення Y1, Y2, ... , Y9 за трьома методиками:
–як середньоарифметичну вихідних показників за даним аспектом якості життя населення;
–як середньозважену оцінку вихідних показників (формула (6.3) п. 6.2.2), де в якості вагових коефіцієнтів використовується частка дисперсії відповідного вихідного показника у сумарній дисперсії усіх вихідних показників за даним аспектом якості життя
(формула (6.4) п. 6.2.2);
–як середньозважену оцінку вихідних показників (формула (6.3) п. 6.2.2), де в якості вагових коефіцієнтів використовуються факторні навантаження, отримані за методом модифікованої головної компоненти. Розрахунок цих факторних навантажень було здійснено за допомогою програмного комплексу SPSS, результати цього розрахунку наведено на листі “розрахунок_SPSS” файла priklad9.xls.
Крок 3. Побудова узагальненого показника якості життя населення Y вищого рівня за формулою (6.12) (див. п. 6.6.2) та визначення рейтингу міст області за якістю життя населення.
150
