
Математичні моделі у фінансах / Рядно О.А. та ін. Математичні моделі у фінансах
.pdf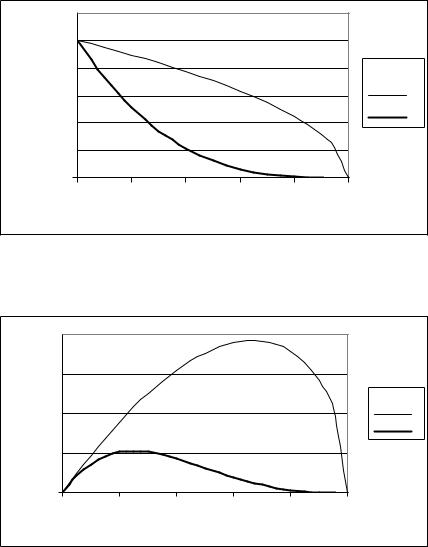
F(x) p x N (1 x). |
(4.29) |
Ця залежність і буде визначати вид кривої Лаффера при зроблених припущеннях (рис.4.5, крива 1).
|
1,2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
n(x)/N |
0,8 |
|
|
|
|
1 |
0,6 |
|
|
|
|
2 |
|
|
|
|
|
|
||
|
0,4 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
|
|
|
x |
|
|
Рис. 4.4. Види залежностей кількості підприємств n(x), які беруть участь у виробництві, від рівня податкової ставки x
|
0,4 |
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
F(x)/ |
0,2 |
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
3 |
|
0,1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
|
|
|
x |
|
|
Рис. 4.5. Форми кривих Лаффера, які відповідають різним типам залежності n(x)
Якщо національна економіка має стабільні темпи зростання, то крива n(x) буде надлінійною („оптимістичною”): при збільшенні
величини податкової ставки x в області 0; xa (xa 1) навіть для досить великих значень xa кількість підприємств, що перестають працювати буде змінюватись незначно. При економічному спаді крива
n(x) буде сублінійною („песимістичною”): навіть |
незначне |
|
збільшення |
податкової ставки x в області 0; xa для |
невеликих |
значень xa |
призводить до значного скорочення кількості працюючих |
|
підприємств.
91
Ці залежності, що графічно представлені на рис. 4.4, можна описати формулою:
n(x) (1 x) , |
(4.30) |
де значення коефіцієнта 1 відповідає „оптимістичній” кривій, значення 1 формує „песимістичну” криву.
Форми кривих Лаффера, які відповідають різним типам залежності n(x), наведено на рис. 4.5. Крива 3 на цьому рисунку відповідає стану макроекономічного зростання, 1 – стану економічного спаду, 2 – проміжний варіант.
У загальному випадку залежність обсягу податкових бюджетних надходжень від величини сукупної податкової ставки (крива Лаффера)
описується, при прийнятих припущеннях, таким рівнянням: |
|
||
|
, , – |
F(x) x (1 x) , |
(4.31) |
де |
коефіцієнти, які задають вид кривої. Економічний |
||
зміст |
коефіцієнта |
– це коефіцієнт податкової прогресії, |
який |
законодавчо закладений в системі оподаткування, коефіцієнт – це коефіцієнт чутливості економіки до зміни податкової ставки (або коефіцієнт згасання економічної активності).
Оптимальне значення сукупної податкової ставки x* для отриманої моделі кривої Лаффера залежить виключно від коефіцієнтів
, :
x* |
|
. |
(4.32) |
|
|||
|
|
|
|
Критерій оптимальності податкової системи може бути сформульований так: податкова система є оптимальною, якщо сукупна податкова ставка x, якою характеризуються взаємовідносини податкової системи з економічним середовищем, дорівнює податковій ставці x* максимуму кривої Лаффера. У протилежному випадку ці взаємовідносини характеризуються слабким (x x*) або надмірним (x x*) податковим навантаженням на економічне середовище. Отже, слід розробляти комплекс правових, економічних та фінансових заходів, які дозволили б зробити різницю x x* мінімальною. У зв’язку з цим виникає задача методично правильного визначення параметрів кривої Лаффера та переходу від абстрактного поняття “сукупна податкова ставка” до конкретних податкових ставок на окремі види податків. Поняття сукупної податкової ставки для національної економіки в цілому є складним. Тому більш доцільним буде поняття “сукупної номінальної податкової ставки”, що є середньою арифметичною зваженою величиною (відповідно до питомої ваги бюджетних надходжень) від наявних номінальних податкових ставок, законодавчо закладених у податкову систему:
92
|
|
x xi |
Fi |
, |
(4.33) |
|
|
F |
|||
|
|
i |
|
|
|
де |
xi – номінальна податкова ставка для i-го типу податку, – |
||||
надходження до |
бюджету від окремого i-го типу |
податку, |
|||
F |
– загальний |
обсяг податкових надходжень до |
бюджету. |
||
Відзначимо, що поняття сукупної номінальної податкової ставки відноситься до певного проміжку часу, протягом якого діють встановлені податкові ставки.
Величину x, що визначено вище, можна ввести в якості незалежної змінної в модель кривої Лаффера.
Зміст представлення x у вигляді (4.33) полягає в тому, що сукупна номінальна податкова ставка подається через реально існуючі податкові ставки на окремі види податків. У цьому разі, при наявності висновку про необхідність зміни сукупної податкової ставки, зрозуміло як саме слід змінювати конкретні реально існуючі податкові ставки на окремі види податків.
Для визначення параметрів кривої Лаффера розглянемо відношення бюджетних податкових надходжень F до обсягу виробленого валового внутрішнього продукту (або валової доданої вартості) V . Це відношення за своєю суттю є так званим податковим навантаженням, яке пов’язане з сукупною податковою ставкою x такою залежністю:
F |
x . |
(4.34) |
|
||
V |
|
|
Відзначимо, що у випадку 1 поняття податкового навантаження та сукупної податкової ставки є тотожними.
Зробимо деякі перетворення рівнянь (4.31), (4.34):
V (1 x) , |
(4.35) |
||
|
F |
x . |
(4.36) |
|
|
||
V |
|
||
Після нескладних перетворень отримаємо систему лінійнологарифмічних рівнянь, які можна використовувати для визначення невідомих параметрів , , :
lnV ln ln(1 x), |
(4.37) |
||
ln |
F |
lnx. |
(4.38) |
|
|||
V |
|
||
Система рівнянь (4.37)-(4.38) може розглядатись як робоча система для визначення параметрів , . Знайшовши конкретне x,
93
при якому знаходиться дана економічна система, та за допомогою системи рівнянь (4.37)-(4.38) визначивши параметри , та
отримавши оптимальне x*, можна шляхом порівняння x та x* зробити висновки про необхідні заходи щодо реформування податкової системи.
У випадку, коли кількість працюючих підприємств при
встановленій сукупній податковій ставці x буде |
визначатися |
||
експоненційним законом згасання економічної активності: |
|
||
n(x) N e x , |
(4.39) |
||
крива Лаффера набуде вигляду: |
|
||
F x e x . |
(4.40) |
||
Для такої моделі максимум податкових надходжень у бюджет |
|||
визначається таким чином: |
|
||
x* |
|
. |
(4.41) |
|
|||
|
|
|
|
Вихідні дані і результати розрахунків. Дані, необхідні для побудови кривої Лаффера для економіки України, наведено на листі “Вихідні дані 1” файла priklad4.xls. Тут, зокрема, наведено щорічні дані по Україні за період з 1999 по 2006 рр. для загальних обсягів податкових надходжень до Зведеного бюджету України, надходжень від податку на прибуток підприємств F1 (млн. грн.), податку з доходів
фізичних |
осіб F2 (млн. грн.), |
податку на |
додану вартість F3 |
(млн. грн.) |
та акцизного збору F4 |
(млн. грн.). |
Тут, також, наведені |
дані по ВВП України у номінальних цінах (млн. грн.) і індексу ВВП у порівняних цінах (%). Використовуючи ці дані, розраховано індекс - дефлятор ВВП як відношення ВВП у номінальних цінах до ВВП у порівняних цінах 1998 р.
Щорічні величини сукупної номінальної податкової ставки x визначено за формулою (4.33), яка у даному випадку набуває вигляду:
x |
x1F1 x2F2 x3F3 x4F4 |
, |
(4.42) |
|
|||
|
F1 F2 F3 F4 |
|
|
причому значення xi брались такими: для податку на прибуток підприємств до 2004 р. x1 0,3, – з 2004 р. x1 0,25; для податку на додану вартість (ПДВ) x3 0,2; величина ставки акцизного збору
94
вибиралась за методом калібрування x4 0,45; величина ставки податку з фізичних осіб x2 визначалась як відношення обсягів надходжень від даного податку за відповідний період до його бази. З
метою врахування інфляційних процесів, значення ВВП |
V та |
||
податкових надходжень F є виправленими з використанням індексу - |
|||
дефлятора і вираженими у їх вартості у 1998 р. |
|
||
На першому етапі аналізу криву Лаффера побудовано для |
|||
випадку, коли 1: |
|
||
|
F(x) x(1 x) |
(4.43) |
|
за формулою: |
|
||
ln |
F |
ln ln(1 x). |
(4.44) |
|
|||
|
x |
|
|
За допомогою функції “ЛИНЕЙН” отримано, що ln 16,1 |
|||
( exp(16,1) 10262689,8), 17,7. Тобто |
побудовано криву |
||||
Лаффера такого вигляду: |
|
|
|
|
|
|
F(x) 10262689,8x(1 x)17,7. |
|
(4.45) |
||
Оптимальна податкова ставка, яка розраховується за формулою |
|||||
(4.32), повинна складати у цьому випадку 5,3%. |
|
|
|
||
Розрахункове значення t – статистики для |
параметра |
, |
|||
обчислене |
за формулою |
(4.15), складає tp 2,24. |
Це менше |
за |
|
табличне |
значення t – |
статистики при 10% |
рівні значимості: |
||
t0,9;6 1,94. Отже, нульову гіпотезу відхилити не можемо, оцінку параметра при 10% рівні значимості не можемо вважати значимою. Спробуємо оцінити криву Лаффера у більш загальному вигляді (4.31).
Для побудови кривої Лаффера у загальному вигляді (4.31) використовувались формули (4.37), (4.38).
Розрахунки параметрів кривої Лаффера виконано за допомогою функції “ЛИНЕЙН”. Оскільки у формулу (4.38), з якої знаходилось значення параметра , константа не входить, при використанні функції “ЛИНЕЙН” параметр функції “Константа” задавався нульовим. Відповідно у цьому випадку функцією “ЛИНЕЙН” середнє
квадратичне відхилення параметра Sa0 |
не |
розраховувалось, а |
||||
кількість |
ступенів |
свободи |
дорівнювала |
k n 1 8 1 7. |
||
Отримано |
такі |
результати: |
1,09; |
ln 16,4 |
||
( exp(16,4) 12804215); |
18,07. |
Тобто побудовано криву |
||||
Лаффера такого вигляду: |
|
|
|
|
||
95
F(x) 12804215 x1,09(1 x)18,07. |
(4.46) |
Розрахункове значення t – статистики для параметра ,
обчислене за формулою (4.15), складає tp 2,28. Це більше за табличне значення t – статистики при 10% рівні значимості: t0,9;6 1,99. Отже, нульову гіпотезу відхиляємо, оцінку параметра
при 10% рівні значимості можемо вважати значимою. Таким чином, проведення розрахунків кривої Лаффера за формулою (4.31) виявилось більш коректним.
Оптимальна податкова ставка, розрахована за формулою (4.32), склала 5,7%. Аналізуючи отриману криву Лаффера та порівнюючи середню величину сукупної номінальної податкової ставки, яка встановлена в Україні (x 0,2) з оптимальною податковою ставкою x* 0,057, розрахованою за формулою (4.32), можна сказати, що при умові збереження пропорцій в ставках на окремі податки та нарахування, кожна з податкових ставок у період, що досліджувався, повинна була бути значно меншою. Отримане нами значення оптимальної сукупної номінальної податкової ставки у три рази менше за встановлене в Україні у 2006 р. Відзначимо, що у роботі [18] розраховано оптимальну величину сукупної номінальної податкової ставки для України у період з січня 1996 по березень 1997 р., яка склала x* 0,08, що у три рази менше за величину, встановлену тоді в Україні (x 0,24). Порівнюючи це значення з отриманим нами, можна зробити висновок, що у період з 1999 по 2006 рр. ситуація не змінилась.
Отримане нами значення 18,07 значно перевищує 1, що може свідчити про те, що у період з 1999 по 2006 рр. [28]економіка України була надзвичайно чутлива до зміни номінальної податкової ставки. У порівнянні з періодом 1996-1997 рр. [16] чутливість економіки суттєво збільшилась.
4.5. Застосування економетричних моделей до аналізу системи виконання доходної частини бюджетів
Вихідні дані та результати розрахунків. Незважаючи на те, що Уряд України проводить інтенсивну роботу по удосконаленню системи управління бюджетними коштами, система виконання бюджетів потребує подальшого реформування. Для комплексного аналізу системи виконання бюджетів, виявлення проблем, що виникають у процесі виконання доходної частини бюджетів, доцільно застосування методів економетричного моделювання.
Проаналізуємо за допомогою економетричних моделей виконання плану щодо надходжень власних доходів загального фонду
96
(доходів без урахування трансфертів) по містах і районах Дніпропетровської області у 2005 р.
На листі “Вихідні дані 1” файлу priklad5.xls наведено заплановані на 2005 р. обсяги власних доходів загального фонду (тис. грн.) та процент їх виконання по містах і районах Дніпропетровської області. Дані наведено як для показників, розрахованих Міністерством фінансів України, так і для показників, уточнених місцевими органами влади. Крім того, наведена кількість населення районів і міст області.
Спочатку проаналізуємо, чи спостерігались у 2005 р. відмінності у виконанні доходів для міст Дніпропетровської області та для сільських районів. Для цього створимо фіктивну змінну gorod , яка приймає значення 1 для міст, та – 0 для сільських районів, і побудуємо залежність показника Y1 – процент виконання плану власних доходів, розрахованого Міністерством фінансів, та показника Y2 – процент виконання плану, уточненого місцевими органами влади, від фактора gorod . Результати розрахунків наведено на листі “Розрахунок11” файла priklad5.xls. За допомогою вбудованої функції Excel “ЛИНЕЙН” побудовано такі рівняння регресії:
Yˆ |
139 |
31 gorod |
|
1 |
|
, |
(4.47) |
|
(39,4) |
||
|
( 4,15) |
|
Yˆ |
110 8 gorod |
|
2 |
. |
(4.48) |
|
(74)( 3,25)
Удужках наведено розраховані за формулою (4.15) розрахункові значення t–статистики. Оцінки усіх параметрів рівнянь (4.47), (4.48) можна вважати значимими, оскільки для них розрахункові значення t-статистики за абсолютною величиною
перевищують критичне значення t0,95;33=2,03 (k n 2 35 2 33, P 1 0,05 0,95) при 5% рівні значимості. Отримані рівняння (4.47), (4.48) означають, що:
|
ˆ |
|
108%, |
ˆ |
|
102% |
для міст області; |
Y |
|
Y |
|
|
|||
|
1 |
|
|
2 |
|
|
(4.49) |
ˆ |
|
|
ˆ |
|
|
||
139%, |
110% |
для сільських районів. |
|||||
Y |
|
Y |
|
|
|||
|
1 |
|
|
2 |
|
|
|
Таким чином, визначено, що рівень виконання доходів бюджетів по містах значно нижчий, ніж по сільських районах області. Причому більша різниця має місце для показників, розрахованих Міністерством фінансів України. Тобто ми бачимо, що план доходів
97

місцевих бюджетів, розрахований Міністерством фінансів, у середньому є заниженим, особливо для сільських районів. Розрахункові значення відсотків виконання доходів по містах і сільських районах Дніпропетровської області наведено на рис. 4.6.
%
160
140
120
100
80
60
40
20
0
Y1розрахунок: місто |
Y1 - розрахунок: сільський район |
Y2розрахунок: місто |
Y2 - розрахунок: сільський район |
Рис. 4.6. Розрахункові значення відсотків виконання доходів по містах
ісільських районах Дніпропетровської області
Уроботі [51] на основі порівняння планування доходів бюджету та їх виконання протягом 1995-2004 рр. зазначається, що в Україні існують серйозні проблеми з плануванням доходної частини бюджету, що, власне, й ускладнює контроль бюджетних видатків. З початку 1997 р. спостерігається така тенденція щодо оцінки доходів: чим вищі заплановані обсяги бюджетних надходжень, тим нижчий рівень виконання бюджету. Перевіримо, чи мала місце ця тенденція для місцевих бюджетів Дніпропетровської області у 2005 р. Для цього проаналізуємо залежність виконання місцевих бюджетів від величини запланованих доходів на душу населення.
Скористаємось даними, наведеними на листі “Вихідні дані 1”
файла priklad5.xls. Створимо нові змінні: X1 – середньодушові заплановані обсяги власних доходів, розраховані Міністерством фінансів України, (грн.), і X2 – середньодушові заплановані обсяги власних доходів, уточнені місцевими органами влади, (грн.), та побудуємо рівняння лінійних регресій Y1 на X1 і Y2 на X2.
Результати розрахунків наведено на листі “Розрахунок12” файла priklad5.xls. За допомогою функції “ЛИНЕЙН” побудовано такі рівняння регресії:
Yˆ |
153 0,0896 X |
1 |
|
|
|
1 |
|
|
, |
(4.50) |
|
|
(18,8) |
( 3,49) |
|
||
|
|
|
|
||
98
Yˆ |
114 |
0,0211 X |
2 |
|
|
2 |
|
|
. |
(4.51) |
|
|
(39,4) |
( 2,55) |
|
||
|
|
|
|
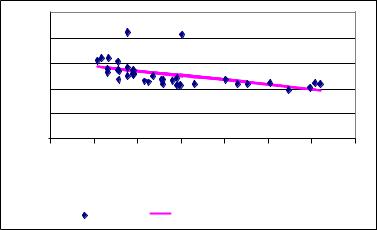
На рис. 4.7, 4.8 наведено діаграми розсіювання та лінії регресії
(4.50), (4.51), що побудовано.
Оскільки розрахункові значення t–статистики для параметрів регресій (4.50), (4.51), що наведені у дужках, за абсолютною величиною перевищують критичне значення t0,95;33=2,03
(k n 2 35 2 33, P 1 0,05 0,95), отримані оцінки для даних параметрів можна вважати значимими при 5% рівні значимості.
На основі рівняння (4.50) можна зробити висновок, що збільшення середньодушового планового обсягу доходів місцевих бюджетів, розрахованого Міністерством фінансів України, на 1 грн., за інших рівних умов призводе до зменшення процента виконання бюджету на 0,09%. Рівняння (4.51) показує, що збільшення середньодушового планового обсягу доходів місцевих бюджетів, уточненого місцевими органами влади, на 1 грн., за інших рівних умов призводе до зменшення процента виконання бюджету на 0,02%. Тут ми знову спостерігаємо, що планові обсяги доходів, розраховані Міністерством фінансів України, чинять більший вплив на виконання доходів, ніж планові обсяги доходів, уточнені місцевими органами влади.
250 |
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
% |
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
|
|
|
грн. |
|
|
|
|
Y1-факт |
Y1-розрахунок |
|
|
|
||
Рис. 4.7. Залежність процента виконання плану власних доходів на 2005 р., розрахованого Міністерством фінансів України, від середньодушових запланованих обсягів доходів
99
140 |
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
% |
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
|
|
|
|
грн. |
|
|
|
|
|
Y2-факт |
|
Y2-розрахунок |
|
|
|||
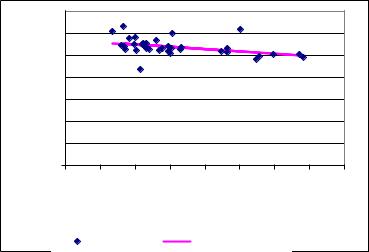
Рис. 4.8. Залежність процента виконання плану власних доходів на 2005 р., уточненого місцевими органами влади, від середньодушових
запланованих обсягів доходів
Тобто аналіз залежності виконання місцевих бюджетів від величини запланованих доходів на душу населення показав, що процент виконання доходів значно залежить від запланованої суми: чим вищі заплановані доходи на душу населення, тим гірше їх виконання. Проведене дослідження свідчить про необхідність більш чіткого планування доходної бази органів місцевого самоврядування. Даний аналіз можливо пояснює і той факт, що рівень виконання доходної частини бюджетів по сільських районах області значно вищий за рівень виконання по містах.
Розглянемо тепер виконання за доходами державного та місцевих бюджетів та проаналізуємо, чи є значна різниця у виконанні доходів Державного та місцевих бюджетів. На листі “Вихідні дані 2” файла priklad5.xls наведено дані щодо плану та фактичного виконання у 2005 р. доходів Зведеного бюджету, а також Державного та місцевих бюджетів по регіонах Дніпропетровської області. Попередній аналіз цих даних показує, що для 5 міст Дніпропетровської області на 2005 р. заплановано (або фактично виконано) від’ємні обсяги доходів Державного бюджету (тобто заплановано надходження не до Державного бюджету, а з Державного бюджету). Для проведення коректного аналізу дані спостережень для цих міст виключимо з розгляду. Створимо змінну Y – відсоток виконання бюджетів області за доходами, для якої маємо 60 даних спостережень: 30 спостережень за відсотком виконання доходів Державного бюджету для 30 регіонів області і 30 спостережень за відсотком виконання місцевих бюджетів, а також
100
