1.11. Максимумы и минимумы функции. Нахождение экстремумов функции

Литература: [3], гл. V, § 3

[5], Ч.1, гл. 6, § 6.3

Точка x₀ называется точкой максимума (минимума) функции y = f (x), если существует такая окрестность точки x₀, что для всех x ≠ x₀ из этой окрестности выполняется неравенство f (x) < f (x₀) (f (x) > f (x₀)).

Точки максимума и минимума функции называются точками экстремума функции, а значения функции в этих точках ─ экстремумами (максимумами и минимумами) функции.

Необходимый признак существования экстремума функции: если непрерывная функция имеет в точке x₀ экстремум, то ее производная в этой точке либо равна нулю, либо не существует.

Внутренние точки области определения функции, в которых производная функции равна нулю или не существует, называются критическими.

Первый достаточный признак существования экстремума: если непрерывная функция y = f (x) дифференцируема в некоторой окрестности точки x₀ при переходе через эту точку (слева направо) производная меняет свой знак плюса на минус, тоx₀ является точкой максимума, если знак меняется с минуса на плюс, то точка x₀ ─ точка минимума. Если знак производной не меняется, то x₀ не является точкой экстремума.

Пример 1. Найти точки экстремума функции

.

Решение. Область определения функции: .

Находим производную функции: .

Находим критические точки: не существует при,при. Критические точкииразбивают область определения функции на интервалы (-∞, 0), (0, 1), (1, +∞).

Определяем знаки производной на каждом из интервалов:

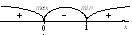
В критической точке производная меняет знак с «+» на «‑». Значит, функция имеет в точкемаксимум. В критической точкезнак производной меняется с «‑» на «+». Следовательно,является точкой минимума функции.

Второй достаточный признак существования экстремума: если в точке x₀ первая производная функции y = f (x) равна нулю, т.е. , а вторая производная функции существует и отлична от нуля, т.е., то точкаx₀ является точкой экстремума. При в точкеx₀ функция имеет максимум, а при ─ минимум. В случае, когдаданный признак не дает ответа на вопрос о существовании экстремума.

Пример 2. Исследовать на экстремум функцию , пользуясь вторым достаточным признаком существования экстремума.

Решение. Область определения функции: .

Находим первую производную функции: .

при , откудаи.

не существует при .

Таким образом, данная функция имеет только одну критическую точку , поскольку точкиине входят в область определения функции.

Находим вторую производную функции: . Вычисляем ее значение в критической точке:. Значит, в точкефункция имеет минимум:.

1.12. Нахождение промежутков выпуклости и вогнутости кривой. Точки перегиба

Литература: [3], гл. V, § 9

[5], Ч.1, гл. 6, § 6.4

Кривая называется выпуклой в интервале (а‚b), если все точки кривой лежат не выше любой ее касательной в этом интервале. Кривая называется вогнутой в интервале (а‚b), если ее точки лежат не ниже любой ее касательной в этом интервале (рис. 1.6).

Для нахождения интервалов выпуклости и вогнутости используется вторая производная функции.

Теорема (достаточный признак выпуклости (вогнутости) кривой): если во всех точках некоторого интервала вторая производная функции y = f (x) отрицательна (положительна), то кривая, описываемая уравнением y = f (x), в этом интервале выпуклая (вогнутая).

Рис. 1.6

Точка кривой М₀(x₀, f (x₀)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.

Теорема (достаточный признак существования точки перегиба): если в точке x₀ вторая производная функции y = f (x) равна нулю или не существует и при переходе через эту точку меняет знак, то точка с абсциссойx = x₀ является точкой перегиба графика функции.

Пример. Найти точки перегиба, интервалы выпуклости и вогнутости кривой .

Решение. Область определения функции: . Находим первую и вторую производные функции:

, .

Обе производные существуют при любых значениях x. Приравняв вторую производную к нулю, находим: x₀ = 2.

Точка x₀ = 2 разбивает область определения функции на интервалы (-∞, 2) и (2, +∞).

Составим таблицу знаков второй производной и поведения функции:

x	(-∞, 2)	2	(2, +∞)
	−	0	+
y	 выпуклая		 вогнутая

Знак второй производной меняется в точке x₀ = 2. Значит, точка кривой является точкой перегиба. Слева от этой точки кривая выпуклая (так как), справа ─ вогнутая (так как).

Итак, интервал выпуклости (-∞, 2), вогнутости (2, +∞).