
- •Программа,
- •Общие указания
- •Программа курса высшей математики (II семестр)
- •Тема 1. Дифференциальное исчисление функций одной переменной
- •Тема II. Исследование функций с помощью производных
- •Тема ііі. Неопределённый интеграл
- •Тема IV. Определённый интеграл
- •Тема V. Несобственные интегралы
- •1.2. Механический и геометрический смысл производной. Уравнения касательной и нормали к кривой
- •1.3. Основные правила дифференцирования
- •1.4. Обратная функция и ее производная
- •1.5. Производная сложной функции
- •1.6. Производные основных элементарных функций.
- •1.7. Производная функции, заданной неявно. Производная степенно-показательной функции. Производная функции, заданной параметрически
- •1.8. Производные высших порядков
- •1.9. Дифференциал функции
- •1.10. Возрастание и убывание функции. Нахождение интервалов монотонности функции
- •1.11. Максимумы и минимумы функции. Нахождение экстремумов функции
- •1.12. Нахождение промежутков выпуклости и вогнутости кривой. Точки перегиба
- •1.13. Асимптоты кривой
- •1.14. Схема полного исследования функции и построение ее графика
- •1.15. Наибольшее и наименьшее значения функции
- •1.16. Применение производной для вычисления пределов (правило Лопиталя)
- •2. Неопределенный интеграл
- •2.1. Первообразная функции и неопределенный интеграл
- •2.2. Таблица основных неопределенных интегралов. Непосредственное интегрирование
- •2.3. Интегрирование методом замены переменной
- •2.4. Метод интегрирования по частям
- •2.5. Интегрирование некоторых функций, содержащих квадратный трехчлен
- •2.6. Интегрирование дробно-рациональных функций
- •2.7. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка
- •2.8. Интегрирование некоторых иррациональных функций. Тригонометрические подстановки
- •2.9. Интегрирование в элементарных функциях
- •3. Определённый интеграл
- •3.1. Задача о площади. Определение определенного интеграла
- •3.2. Основные свойства определенного интеграла
- •3.3. Вычисление определенного интеграла. Формула Ньтона-Лейбница
- •3.4. Замена переменной в определенном интеграле
- •3.5. Интегрирование по частям
- •3.6.2. Вычисление длин дуг плоских кривых
- •3.6.3. Вычисление объемов тел вращения
- •3.6.4. Вычисление площадей поверхностей тел вращения
- •4. Несобственные интегралы
- •4.1. Несобственные интегралы первого рода
- •Пусть подынтегральная функция f (X)имеет первообразную f (X). Тогда согласно формуле Ньютона-Лейбница и определению несобственного интегралабудем иметь
- •4.2. Несобственные интегралы второго рода
- •Используя определение, находим
- •Т.Е. Этот несобственный интеграл является расходящимся. В общем случае нетрудно доказать, что несобственный интеграл второго рода сходится прии расходится при.
- •Задания для контрольных работ Контрольная работа № 3 «Производная»
- •Контрольная работа № 4 «Неопределенный и определенный интегралы»
1.15. Наибольшее и наименьшее значения функции
Литература: [3], гл. V, §§ 6, 7
[5], Ч.1, гл. 6, § 6.7
Наибольшее (наименьшее) значение непрерывной функции на замкнутом промежутке [a, b] достигается или в точках экстремума, или на концах этого промежутка. Для определения наибольшего (наименьшего) значения нужно вычислить значение функции во всех критических точках, принадлежащих промежутку [a, b], значение функции на концах промежутка и взять наибольшее (наименьшее) из них.
Замечание. Если внутри некоторого промежутка непрерывная функция имеет только одну точку экстремума и это точка максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение на промежутке.
Пример 1.
Найти наибольшее и наименьшее значения
функции
![]() на промежутке
на промежутке![]() .
.
Решение. Найдём
производную:
![]() .
.
Одна критическая
точка ─ x1
= 0 (в ней производная не существует).
Остальные критические точки находятся
из равенства:
![]() ,
откудаx2
= 1 и x3
= −1. Точка x3
= −1 не принадлежит промежутку
,
откудаx2
= 1 и x3
= −1. Точка x3
= −1 не принадлежит промежутку
![]() и из дальнейшего рассмотрения исключается.
и из дальнейшего рассмотрения исключается.
Вычисляем значения
функции в точках x1,
x2
и на концах промежутка:
![]() .
.
Из полученных
значений выбираем наименьшее и наибольшее:
![]() и
и![]() .
.
Пример 2. Определить размеры открытого бассейна с квадратным дном объёмом V так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
Решение.
Обозначим сторону основания через х,
а высоту – через у.
Тогда объём бассейна
![]() ,
а облицовываемая поверхность
,
а облицовываемая поверхность![]() .
Выразим из значениеу
через х:
.
Выразим из значениеу
через х:
![]() .
Подставляя это значениеу
в выражение для S,
получим
.
Подставляя это значениеу
в выражение для S,
получим
![]() .
.
Исходя из условия задачи и вида функции S = S(х), эта функция имеет смысл при х > 0, т.е. в промежутке (0, +∞). Исследуем функцию на минимум в этом промежутке.
![]() .
.
Для исследования полученной критической точки на экстремум вычислим в ней вторую производную:
![]() .
.
Так как вторая производная в критической точке положительна, то функция S(х) имеет в ней минимум, а так как на промежутке (0, +∞) это единственный экстремум, то это и наименьшее значение.
Итак, при стороне
основания
![]() и высоте
и высоте![]() площадь облицовкиS
будет наименьшей.
площадь облицовкиS
будет наименьшей.
1.16. Применение производной для вычисления пределов (правило Лопиталя)
Литература: [5], Ч.1, гл. 5, § 5.5
Теорема Лопиталя.
Если функции y
= f
(x)
и y
= φ
(x)
дифференцируемы в окрестности точки x
= x0
и непрерывны в самой точке x0,
обе стремятся к нулю (или к ±∞) при x
→ x0,
и существует
![]() ,
топредел
отношения функций
f
(x)
и φ
(x)
при x
→ x0
равен пределу
отношения их производных
при x
→ x0,
т.е.
,
топредел
отношения функций
f
(x)
и φ
(x)
при x
→ x0
равен пределу
отношения их производных
при x
→ x0,
т.е.
![]() .
.
Заметим, что теорема (правило) Лопиталя справедлива и при x → ±∞.
Из теоремы Лопиталя
следует, что она применяется в случае,
когда предел отношения двух функций
представляет собой неопределённость
вида
![]() или
или![]() .
Заметим также, что если предел частного
.
Заметим также, что если предел частного![]() так же даёт неопределённость указанного
вида и функции
так же даёт неопределённость указанного
вида и функции![]() и
и![]() удовлетворяют условиям теоремы Лопиталя,
то можно перейти к отношению вторых
производных и т.д.
удовлетворяют условиям теоремы Лопиталя,
то можно перейти к отношению вторых
производных и т.д.
Пример 1.
Найти
![]() .
.
Решение. Числитель и знаменатель данной дроби непрерывны, дифференцируемы и стремятся к нулю при x → 0. Это означает, что можно применить правило Лопиталя:
![]() .
.
Замечание 1.
Для раскрытия неопределённостей вида
![]() или
или![]() их нужно привести к виду
их нужно привести к виду![]() или
или![]() ,
а затем применять правило Лопиталя.
,
а затем применять правило Лопиталя.
Замечание 2.
В случае неопределённостей вида
![]() ,
,![]() или
или![]() целесообразно предварительно
прологарифмировать заданное выражение.
целесообразно предварительно
прологарифмировать заданное выражение.
Пример 2.
Вычислить
![]() .
.
Решение. Имеем
неопределённость вида
![]() .
Преобразуем её к виду
.
Преобразуем её к виду![]() и применим правило Лопиталя:
и применим правило Лопиталя:
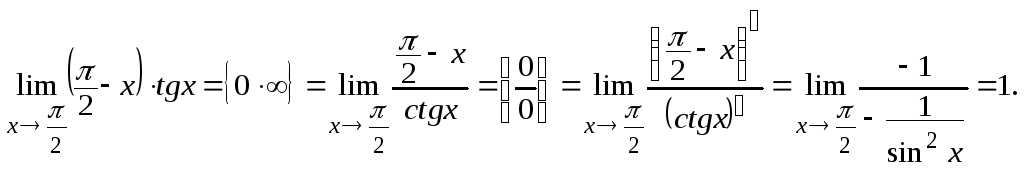
Пример 3.
Вычислить
![]() .
.
Решение. Имеем
неопределённость вида
![]() .
Пусть
.
Пусть![]() .
Тогда
.
Тогда
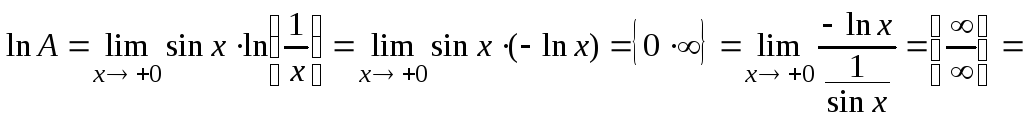
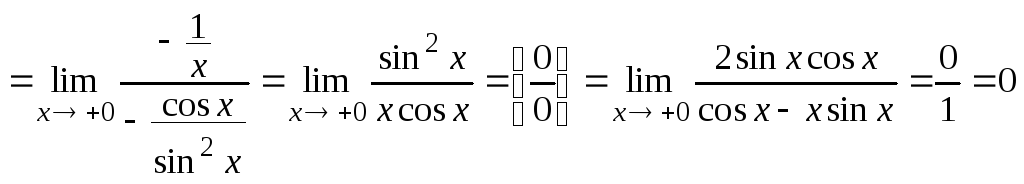 .
.
Итак,
![]() .
Следовательно,
.
Следовательно,![]() .
.
Замечание 3. Иногда правило Лопиталя применяется несколько раз.
Пример 4.
Вычислить
![]() .
.
Решение.
![]()
![]() .
.
