
- •Программа,
- •Общие указания
- •Программа курса высшей математики (II семестр)
- •Тема 1. Дифференциальное исчисление функций одной переменной
- •Тема II. Исследование функций с помощью производных
- •Тема ііі. Неопределённый интеграл
- •Тема IV. Определённый интеграл
- •Тема V. Несобственные интегралы
- •1.2. Механический и геометрический смысл производной. Уравнения касательной и нормали к кривой
- •1.3. Основные правила дифференцирования
- •1.4. Обратная функция и ее производная
- •1.5. Производная сложной функции
- •1.6. Производные основных элементарных функций.
- •1.7. Производная функции, заданной неявно. Производная степенно-показательной функции. Производная функции, заданной параметрически
- •1.8. Производные высших порядков
- •1.9. Дифференциал функции
- •1.10. Возрастание и убывание функции. Нахождение интервалов монотонности функции
- •1.11. Максимумы и минимумы функции. Нахождение экстремумов функции
- •1.12. Нахождение промежутков выпуклости и вогнутости кривой. Точки перегиба
- •1.13. Асимптоты кривой
- •1.14. Схема полного исследования функции и построение ее графика
- •1.15. Наибольшее и наименьшее значения функции
- •1.16. Применение производной для вычисления пределов (правило Лопиталя)
- •2. Неопределенный интеграл
- •2.1. Первообразная функции и неопределенный интеграл
- •2.2. Таблица основных неопределенных интегралов. Непосредственное интегрирование
- •2.3. Интегрирование методом замены переменной
- •2.4. Метод интегрирования по частям
- •2.5. Интегрирование некоторых функций, содержащих квадратный трехчлен
- •2.6. Интегрирование дробно-рациональных функций
- •2.7. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка
- •2.8. Интегрирование некоторых иррациональных функций. Тригонометрические подстановки
- •2.9. Интегрирование в элементарных функциях
- •3. Определённый интеграл
- •3.1. Задача о площади. Определение определенного интеграла
- •3.2. Основные свойства определенного интеграла
- •3.3. Вычисление определенного интеграла. Формула Ньтона-Лейбница
- •3.4. Замена переменной в определенном интеграле
- •3.5. Интегрирование по частям
- •3.6.2. Вычисление длин дуг плоских кривых
- •3.6.3. Вычисление объемов тел вращения
- •3.6.4. Вычисление площадей поверхностей тел вращения
- •4. Несобственные интегралы
- •4.1. Несобственные интегралы первого рода
- •Пусть подынтегральная функция f (X)имеет первообразную f (X). Тогда согласно формуле Ньютона-Лейбница и определению несобственного интегралабудем иметь
- •4.2. Несобственные интегралы второго рода
- •Используя определение, находим
- •Т.Е. Этот несобственный интеграл является расходящимся. В общем случае нетрудно доказать, что несобственный интеграл второго рода сходится прии расходится при.
- •Задания для контрольных работ Контрольная работа № 3 «Производная»
- •Контрольная работа № 4 «Неопределенный и определенный интегралы»
1.9. Дифференциал функции
Литература: [5], Ч.1, гл. 5, §§ 5.3, 5.4
Пусть функция y
= f
(x)
дифференцируема на отрезке [a‚
b].
Производная этой функции в некоторой
точке x
отрезка [a‚
b]
определяется равенством
![]() .
.
На основании
свойства функции, имеющей конечный
предел, имеем
![]() ,
где
,
где![]() ─ бесконечно малая более высокого
порядка, чем
─ бесконечно малая более высокого
порядка, чем![]() ,
т.е.
,
т.е.![]() .
.
Тогда
![]()
или
![]() .
.
Таким образом,
приращение функции
![]() представлено в виде суммы двух слагаемых,
одно из которых
представлено в виде суммы двух слагаемых,
одно из которых![]() линейное относительно
линейное относительно![]() и является главной частью приращения
функции, если
и является главной частью приращения
функции, если![]() ,
а второе
,
а второе![]() ─ бесконечно малая более высокого
порядка малости по сравнению с
─ бесконечно малая более высокого
порядка малости по сравнению с![]() .
.
Дифференциалом
(первого
порядка) функции y
= f
(x)
называется главная часть ее приращения,
линейная относительно приращения
аргумента
![]() .
.
Дифференциал
аргумента равен приращению аргумента
![]()
Дифференциал
функции равен произведению ее производной
на дифференциал аргумента:
![]() .
.
Геометрически
дифференциал представляет собой
приращение ординаты касательной к
графику функции в точке
![]() (рис. 1.4).
(рис. 1.4).

Рис. 1.4
Основные свойства дифференциала:
1)
![]() ,
где
,
где![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() .
.
Последнее свойство называется свойством инвариантности формы первого дифференциала, здесь u ─ не независимая переменная, а дифференцируемая функция.
Если приращение
![]() аргумента мало по абсолютной величине,
то
аргумента мало по абсолютной величине,
то![]() и
и![]() Таким образом, дифференциал функции
может применяться для приближенных
вычислений.
Таким образом, дифференциал функции
может применяться для приближенных
вычислений.
Дифференциалом
второго порядка
функции y
= f
(x)
называется дифференциал от дифференциала
первого порядка:
![]() Аналогично определяетсядифференциал
третьего порядка:
Аналогично определяетсядифференциал
третьего порядка:
![]() Вообще,
Вообще,![]()
Если y = f (x) и x − независимая переменная, то дифференциалы высших порядков вычисляются по формулам
![]() ,
,
![]() ,
… ,
,
… ,![]() .
.
Пример.
Найти дифференциал функции
![]() .
.
Решение.
![]() .
.
1.10. Возрастание и убывание функции. Нахождение интервалов монотонности функции
Литература: [5], Ч.1, гл. 6, § 6.2
Функция y = f (x) называется возрастающей в интервале (а‚ b), если большему значению аргумента соответствует большее значение функции, т.е. для любых x1 и x2 из интервала (а‚ b) таких, что x2 > x1, выполняется неравенство f (x2) > f (x1) (рис. 1.5, а). Функция y = f (x) называется неубывающей, если f (x2) ≥ f (x1).
Функция y = f (x) называется убывающей в интервале (а‚ b), если большему значению аргумента (x2 > x1) соответствует меньшее значение функции (f (x2) < f (x1)) (рис. 1.5, б). Функция y = f (x) называется невозрастающей, если f (x2) ≤ f (x1).
Интервалы возрастания и убывания функции называются интервалами монотонности.
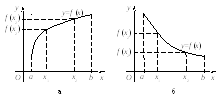
Рис. 1.5. Графики возрастающей (а) и убывающей (б)
в интервале (а‚ b) функций
Достаточный
признак возрастания (убывания) функции:
если дифференцируемая в интервале (а‚
b)
функция имеет положительную (отрицательную)
производную для всех x![]() (а‚
b),
то она возрастает (убывает) в этом
интервале.
(а‚
b),
то она возрастает (убывает) в этом
интервале.
Пример. Найти интервалы монотонности функции
![]() .
.
Решение. Функция
определена на всей числовой оси:
![]() .
Находим производную заданной функции:
.
Находим производную заданной функции:
![]() .
.
Знаки производной определяем методом интервалов:

Таким образом,
функция убывает на интервале (1, 3) и
возрастает на (-∞, 1)
![]() (3, +∞).
(3, +∞).
