2.9. Интегрирование в элементарных функциях

Литература: [3], гл. X, § 16

Как было сказано в п. 2.1, всякая функция f (x), непрерывная на [a, b], имеет на этом промежутке первообразную. Однако не всякая первообразная является элементарной функцией.

Например, функция непрерывна на всей числовой прямой, следовательно, её первообразная, а, значит, и , существует на любом промежутке. Но в элементарных функциях первообразная этой функции не выражается.

О функциях, первообразные которых существуют, но не являются элементарными функциями, говорят, что они не интегрируемы в элементарных функциях. А интегралы от таких функций называются неберущимися в элементарных функциях.

К таким интегралам относятся, например: ,,,,и т.д.

3. Определённый интеграл

3.1. Задача о площади. Определение определенного интеграла

Литература: [3], гл. XI, §§ 1, 2

[5], Ч.2, гл. 10, § 10.1

На плоскости введём прямоугольную декартову систему координат Oxy. Рассмотрим функцию y = f (x), непрерывную и неотрицательную для любых x из отрезка [a, b] (рис. 3.1).

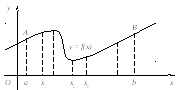
Рис. 3.1

Фигуру aABb, ограниченную снизу отрезком [a, b] оси Ox, сверху дугой AB графика функции y = f (x), а слева и справа отрезками прямых x=a и x=b, назовем криволинейной трапецией.

Разобьем отрезок [a, b] произвольным образом на n частей, абсциссы точек деления обозначим следующим образом:

a = x₀ < x₁ < x₂ <…< x_n-1 < x_n = b.

Через точки x_k проведем прямые x = x_k , которые разобьют криволинейную трапецию на n полос, каждая из которых также является криволинейной трапецией с основанием [x_k-1; x_k] (k = 1, 2, …, n). Площадь трапеции aABb будет равна сумме площадей n полос, ее составляющих. Если n достаточно велико, а все отрезки [x_k-1; x_k] малы, то площадь каждой полосы можно заменить площадью соответствующего прямоугольника с высотой, равной f (с_k), где с_k – произвольная точка на отрезке [x_k-1; x_k]. В силу непрерывности функции f (x) значения f (x) на каждом отрезке [x_k-1; x_k] мало изменяются. Поэтому на каждом отрезке функцию f (x) можно считать постоянной и равной f (с_k). Так что площадь одной полосы приближенно равна f (с_k)∙(x_k-1; x_k). Тогда для площади криволинейной трапеции aABb получим приближенное равенство:

.

Обычно разности (x_k − x_k-1) обозначают через Δx_k, а называют диаметром разбиения. По определению,площадью S криволинейной трапеции называется предел суммы S_n площадей прямоугольников при стремлении диаметра разбиения к нулю, т.е.

.

Сумма называетсяn-ой интегральной суммой для функции y = f (x) на отрезке [a; b].

Определенным интегралом от функции y = f (x) на отрезке [a; b] называется предел интегральной суммы S_n при неограниченном увеличении числа частичных отрезков и стремлении к нулю наибольшей из длин частичных отрезков (если этот предел существует, конечен и не зависит ни от способа разбиение отрезка [a; b] на частичные отрезки ни от выбора точек с_k в них):

.

В случае существования такого предела функция f (x) называется интегрируемой на отрезке [a; b]. Числа a и b называются, соответственно, нижним и верхним пределами интегрирования. При постоянных пределах интегрирования определенный интеграл представляет собой постоянное число и не зависит от того, какой буквой обозначена переменная интегрирования:

.

Необходимым условием интегрируемости на отрезке [a; b] функции y = f (x) является ее ограниченность. Поэтому в дальнейшем мы будем наперед предполагать функцию f (x) ограниченной, т.е. , если.

Достаточным условием интегрируемости функции f (x) на [a; b] является ее непрерывность. Но можно доказать, что если функция f (x) на отрезке [a; b] имеет конечное число точек разрыва первого рода, то она также интегрируема.

Геометрический смысл определенного интеграла следует из рассмотренной задачи: если функция y = f (x) интегрируема и неотрицательна на [a; b], то равен площади криволинейной трапеции, ограниченной линиямиy = f (x), y=0, x=a, x=b.