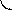1.13. Асимптоты кривой

Литература: [3], гл. V, § 10

[5], Ч.1, гл. 6, § 6.5

Прямая называется асимптотой кривой y = f (x), если расстояние от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность от начала координат (рис. 1.7).

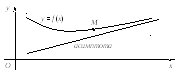
Рис. 1.7

Различают вертикальные и наклонные асимптоты. Вертикальная асимптота имеет уравнение вида x = x₀ и является прямой, параллельной оси Оy. Наклонная асимптота имеет уравнение вида y = k x + b. В частном случае при k = 0 асимптота называется горизонтальной, так как ее уравнение y = b есть прямая, параллельная оси Ох.

Вертикальные асимптоты.

Пусть дана кривая y = f (x). Для нахождения вертикальной асимптоты этой кривой находят точки ее бесконечного разрыва (точки разрыва второго рода).

Если, например,

и ,

то прямая x = x₀ ─ вертикальная асимптота кривой y = f (x) (рис. 1.8).

Наклонные и горизонтальные асимптоты.

Пусть задана кривая y = f (x). Для нахождения наклонной асимптоты, уравнение которой y = k x + b, находят коэффициенты k и b, вычисляя пределы: ,. Эти пределы вычисляются отдельно для случаеви. Если хотя бы один из пределов для вычисленияk и b равен ∞ или не существует, то кривая наклонных и горизонтальных асимптот не имеет.

В частном случае, когда k = 0, а b ─ конечное число, кривая имеет горизонтальную асимптоту, уравнение которой y = b.

Пример. Найти асимптоты кривой .

Решение. Функция определена на всем множестве действительных чиселR, кроме точки x = 1. Определим характер разрыва, для чего вычислим пределы функции при x → 1 слева (x < 1) и справа (x > 1):

, .

Так как один из пределов бесконечен, то x = 1 является точкой разрыва второго рода, и, следовательно, кривая имеет вертикальную асимптоту x = 1.

Определим, имеет ли кривая наклонную или горизонтальную асимптоту. Для этого вычисляем соответствующие пределы:

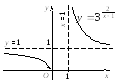, Уравнение асимптотыy = k x + b принимает вид y = 1 (горизонтальная асимптота).

С

Рис. 1.9

хематический график функции представлен на рис. 1.9.

1.14. Схема полного исследования функции и построение ее графика

Литература: [3], гл. V, § 11

[5], Ч.1, гл. 6, § 6.6

1. Находим область определения функции.

2. Устанавливаем четность, нечетность функции, периодичность. Находим характерные точки, например, точки пересечения с осями координат.

3.Находим точки разрыва функции, определяем их характер. При наличии точек разрыва второго рода (точек бесконечного разрыва) устанавливаем наличие вертикальных асимптот графика функции.

4. Находим производную функции, критические точки, промежутки монотонности, точки экстремума и значения функции в этих точках.

5. Находим вторую производную функции, интервалы выпуклости и вогнутости кривой и точки перегиба графика функции.

6.Устанавливаем наличие у исследуемой кривой наклонных и горизонтальных асимптот.

7. По полученным данным строим график функции.

Замечание. Если функция является четной или нечетной, то исследование проводят не на всей числовой оси, а на промежутке [0, +∞). Затем график продолжают симметрично относительно оси ординат на промежуток (-∞, 0), если функция четная, и относительно центра системы координат, если функция нечетная.

Если функция периодическая, то ее график строят для одного периода, а затем периодически продолжают на всю числовую ось.

Пример. Провести полное исследование функции и построить ее график.

Решение.

1. Функция определена и непрерывна на всей числовой оси, кроме точек x = ± 2.

2. Функция нечетная, так как для нее выполняется условие . Поэтому достаточно провести исследование на промежутке [0, +∞).

3. В промежутке [0, +∞) имеется одна точка разрыва x = 2. Исследуем характер точки разрыва, для чего вычислим следующие пределы:

,

Так как односторонние пределы бесконечные, то прямая x = 2 является вертикальной асимптотой.

4. Находим первую производную:

.

Находим критические точки на промежутке [0, +∞): ,. В точкепроизводная не существует, но эта точка не является критической, так как функция в ней не определена.

5. Находим вторую производную:

.

Вторая производная на промежутке [0, +∞) обращается в ноль в точке x₁ = 0 и не существует в точке x₃ = 2, которая не входит в область определения функции.

По полученным данным строим таблицу:

x	0	(0, 2)	2	(2, )
	0	−	Не существует	–	0	+
	0	−	Не существует	+	+	+
y	0		Не существует		min

В первой строке таблицы указаны интервалы, на которые критические точки и точки, где вторая производная равна нулю или не существует, разбивают промежуток [0, +∞). Во второй строке указан знак первой производной в этих интервалах, в третьей − знак второй производной. В четвертой строке условно изображено возрастание или убывание функции на промежутке (по знаку первой производной), и выпуклость или вогнутость кривой (по знаку второй производной).

6. Ищем наклонную асимптоту:

,

.

Кривая на промежутке [0, +∞) имеет наклонную асимптоту .

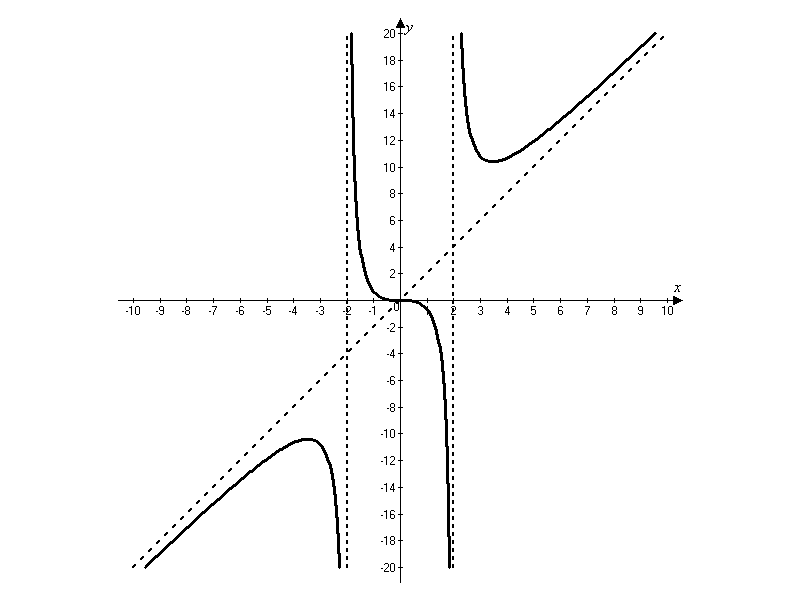
Строим вертикальную x = 2 и наклонную y = 2x асимптоты, а затем по данным таблицы строим график исследуемой функции на промежутке [0, +∞), который затем продолжаем на промежуток (-∞, 0) симметрично относительно центра системы координат.