1.3. Основные правила дифференцирования

Теорема 1. Если функции идифференцируемы в данной точке, то в той же точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых:

.

Формула обобщается на случай любого конечного числа слагаемых.

Теорема 2. Если функции идифференцируемы в данной точкех, то в этой же точке дифференцируемо и их произведение, при этом:

.

Следствие. Постоянный множитель можно выносить за знак производной:

, где .

Теорема 3. Если в данной точке х функции идифференцируемы и, то в той же точке дифференцируемо и их частное, причем

.

1.4. Обратная функция и ее производная

Рассмотрим функцию y = f (x) с областью определения (a, b) и множеством значений (c, d). Пусть эта функция такова, что всякая прямая, проходящая через точку интервала (c, d) параллельно оси Ох, пересекает ее график только в одной точке, т.е. уравнение y = f (x) для каждого y(c, d) определяет единственное значение x(a, b). В этом случае каждому значению y(c, d) соответствует единственное значение x(a, b), т.е. на интервале (c, d) задана функция, множество значений которой есть интервал (a, b). Эта функция называется обратной по отношению к функции y = f (x) и обозначается . Очевидно, что для функцииобратной является функция. Поэтому обе эти функции называютсявзаимно обратными.

Теорема. Если функция y = f (x) монотонна и дифференцируема в некотором интервале и имеет в точке x этого интервала производную , не равную нулю, то обратная функцияв соответствующей точкеy имеет производную, причем или иначе.

1.5. Производная сложной функции

Если и, тоестьсложная функция независимого аргумента x с промежуточным аргументом u.

Теорема. Если имеет производнуюв точкеx, а функция имеет производнуюв соответствующей точкеu, то сложная функция в данной точкеx имеет производную , которая находится по следующей формуле.

Часто пользуются следующей формулировкой этой теоремы: производная сложной функции равна произведению производной внешней функции по промежуточному аргументу на производную внутренней функции по независимому аргументу.

Сложная функция может быть составлена не из двух функций, а из большого их числа. В таких случаях теорема применяется последовательно несколько раз.

В частности, если функция такова, что,,, то производнаянаходится по формуле.

1.6. Производные основных элементарных функций.

Таблица производных

Используя определение производной, можно найти производные основных элементарных функций.

1. Производная степенной функции .

2. Производная показательной функции .

В частности, .

3. Производная логарифмической функции , ,. В частности,.

4. Производные тригонометрических функций ,,,.

Найдем, например, производную функции . По определению производной имеем:

.

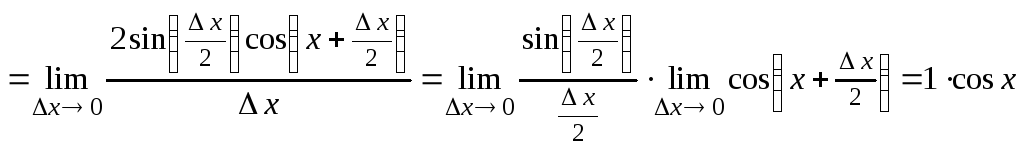Производную функции можно найти по правилу дифференцирования частного двух функций:

.

5. Производные обратных тригонометрических функций ,.

Найдем, например, производную функции . Функция,обратная к функции,. По правилу дифференцирования обратной функции. На интервалеимеем .

Запишем таблицу производных для где.

1.	8.
2.	9.
3.	10.
4.	11.
5.	12.
6.	13.
7.	14.

Применяя формулы и правила дифференцирования, найдем производные следующих функций:

1) .

Применим правило дифференцирования произведения двух функций:

.

2) .

Применим правило дифференцирования частного двух функций:

.

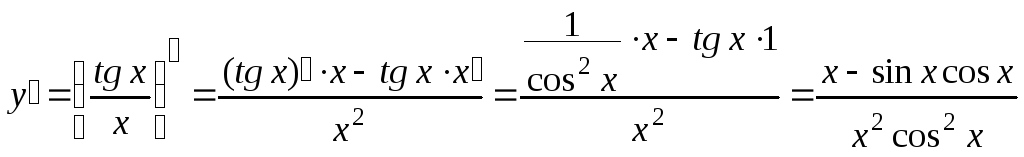3) .

Применим правило дифференцирования сложной функции:

.
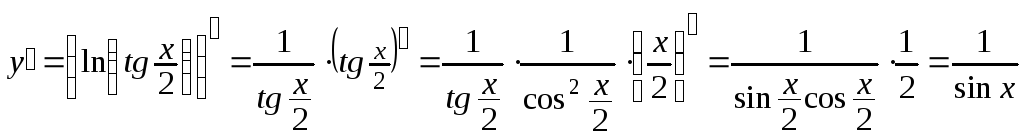