2.7. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка

Литература: [3], гл. X, § 14

[5], Ч.2, гл. 9, § 9.5

Рассмотрим интеграл , где .

.

Последний интеграл можно разложить на сумму интегралов вида .

Аналогично можно найти , где.

Пример 1.

.

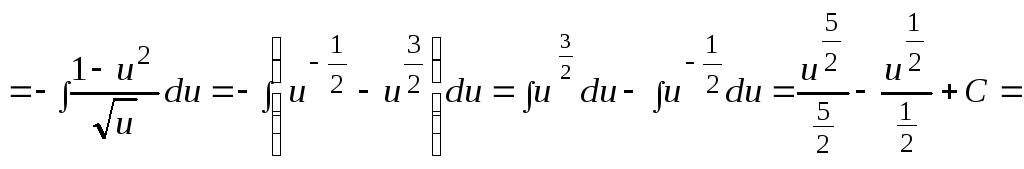
Рассмотрим интеграл , гдеm, n – целые неотрицательные числа. Степень подынтегральной функции понижают с помощью формул:

, ,.

Пример 2.

.

Рассмотрим интеграл , где,.

Здесь используется тригонометрическая формула .

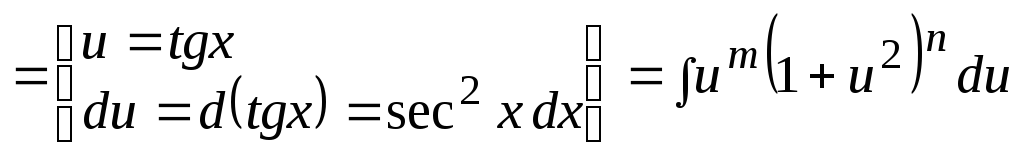
Последний интеграл можно представить в виде суммы интегралов вида .

Аналогично можно найти где,, используя формулу.

Пример 3.

.

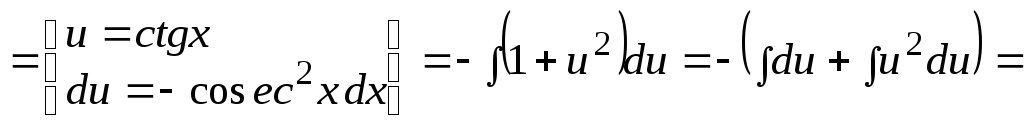
Рассмотрим интеграл , гдеm=2, 3, 4, 5…

.

Если не является табличным (приm−2>1), к нему снова применяют этот метод.

Аналогично можно найти , гдеm=2, 3, 4, 5, …

Пример 4.

.

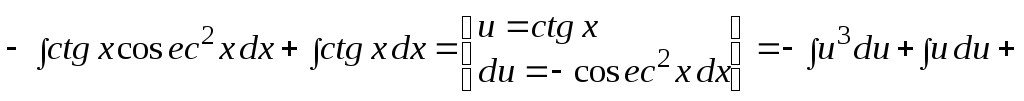
Интегралы вида: ,,легко сводятся к табличным интегралам после применения формул:

,

,

.

Пример 5.

.

Интеграл , гдеможно свести к сумме табличных или рассмотренных интегралов, если заменить в числителе.

Пример 6.

.

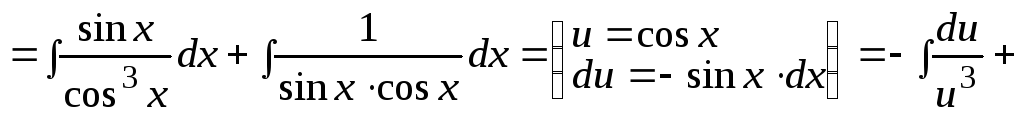
Рассмотрим наиболее общий метод интегрирования функций, рациональных относительно и.

Примеры таких функций ,и т.д.

Функция не является рациональной относительно, т.к. в неёвходит в степени.

С помощью универсальной тригонометрической подстановки функция, рациональная относительнои, сводится к функции, рациональной относительноt. При этом:

, ,,.

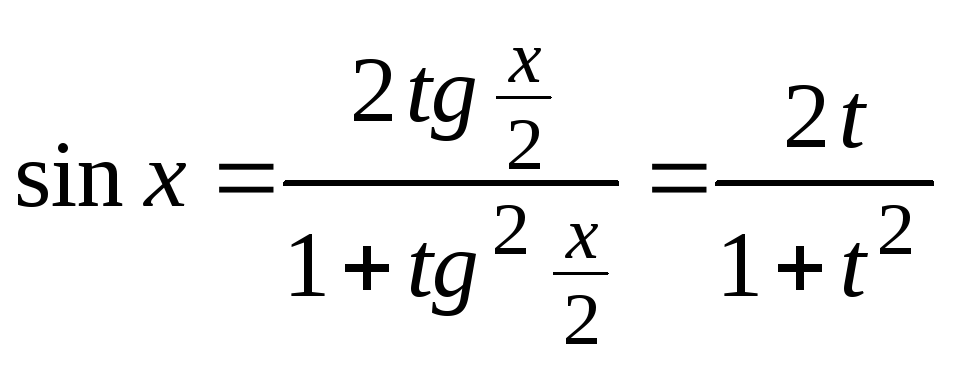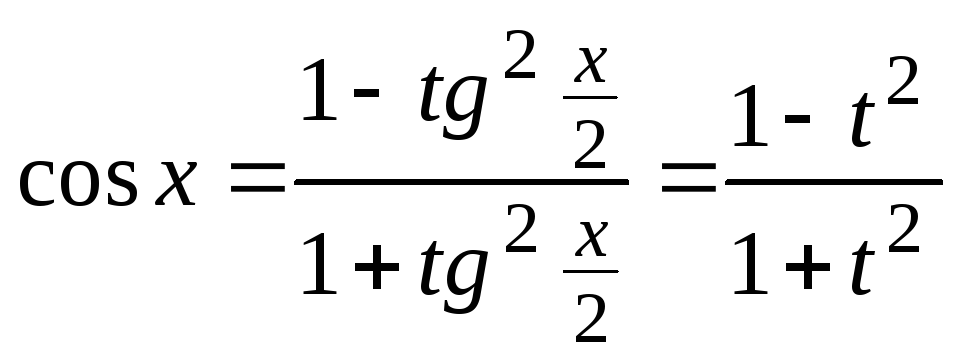Тогда , гдеR₁(t) – функция, рациональная относительно t. Интегрирование таких функций рассмотрено в п. 2.6.

Пример 7.

.

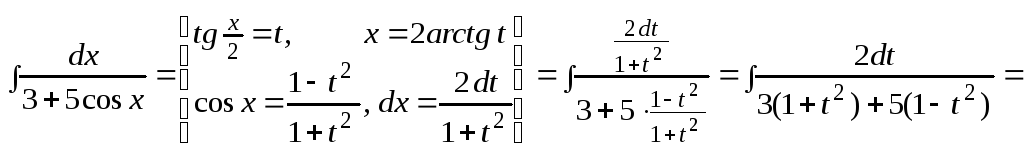
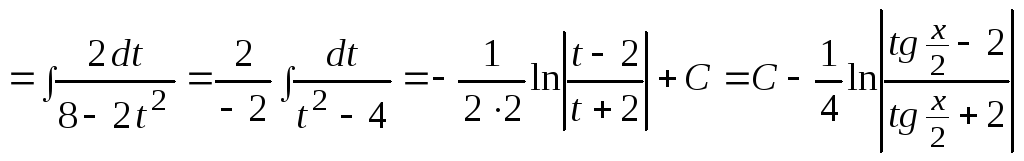Пример 8.

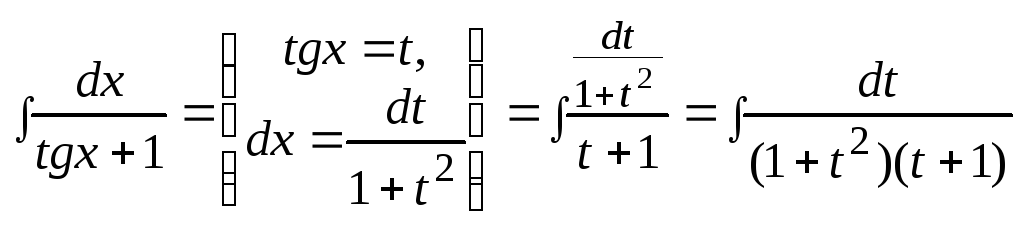
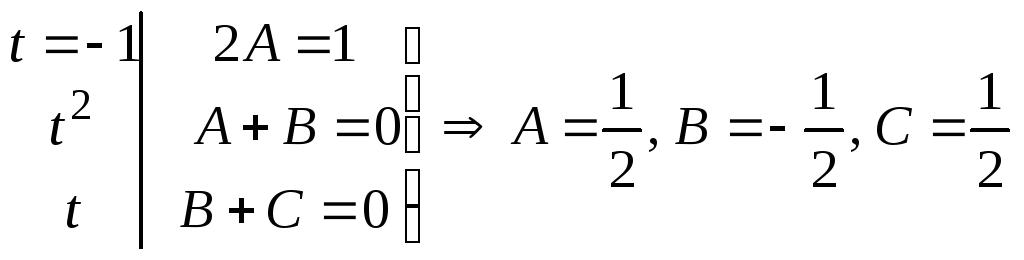
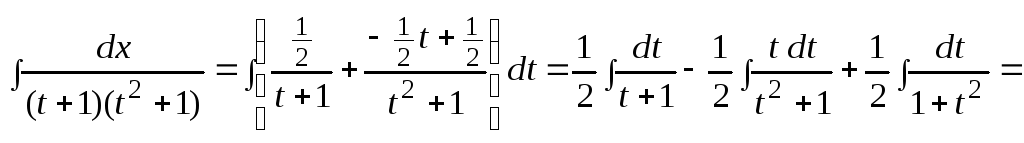
2.8. Интегрирование некоторых иррациональных функций. Тригонометрические подстановки

Литература: [3], гл. X, §§ 11, 14

[5], Ч.2, гл. 9, § 9.5

Рассмотрим некоторые типы интегралов, содержащие иррациональные выражения.

1) , гдеR – рациональная функция своих аргументов.

Пусть k – наименьший общий знаменатель дробей (другими словамиk – наименьшее общее кратное натуральных чисел n, q, …, s). Сделаем подстановку: ,. Тогда каждая дробная степеньx выражается через целую степень t и, следовательно, подынтегральная функция преобразуется в рациональную функцию относительно t (многочлен или рациональную дробь), методы интегрирования которой рассмотрены выше.

Пример 1.

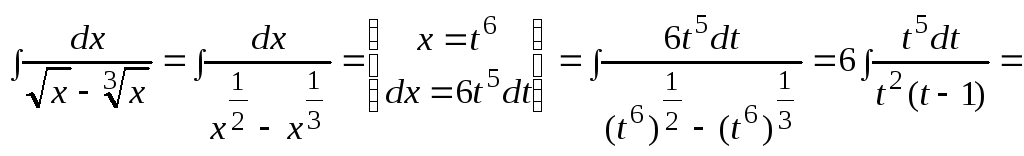
2) , гдеR – рациональная функция своих аргументов, .

Пусть , гдеk – как и прежде, наименьший общий знаменатель дробей . Тогда. С помощью такой подстановки подынтегральная функция преобразуется в рациональную функцию относительноt.

Пример 2.

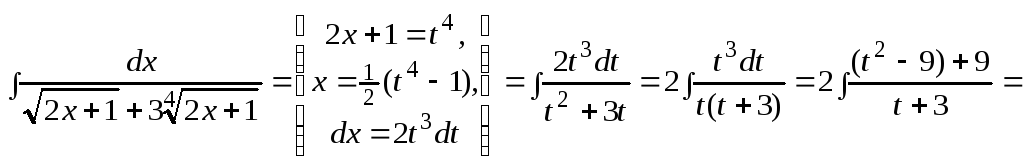
3) , гдеR – рациональная функция своих аргументов, .

Подынтегральную функцию можно рационализировать с помощью подстановки , откуда,.

Рассмотрим теперь интегралы вида , ,, гдеR – функция, рациональная относительно своих аргументов. Если интегралы не являются табличными, то избавиться в подынтегральной функции от квадратного корня можно с помощью, так называемых, тригонометрических подстановок.

4) .

Пусть , тогда, .

Пример 3.

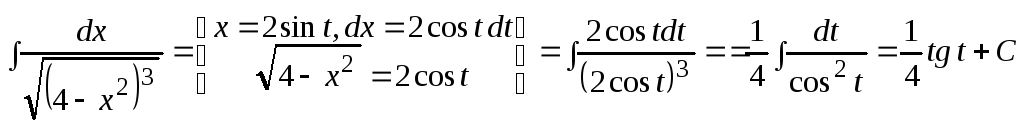
Теперь в ответе надо перейти к х. Это удобнее всего сделать с помощью прямоугольного треугольника. Из подстановки находим. Вспоминаем, что в прямоугольном треугольникеравен отношению противолежащего катетах к гипотенузе 2. По теореме Пифагора находим третью сторону треугольника, а затем по этому треугольнику можно находить любую тригонометрическую функцию угла t.

Из рисунка видно , .

Итак, .

5) .

Пусть , тогда,, .

Пример 4.

, .

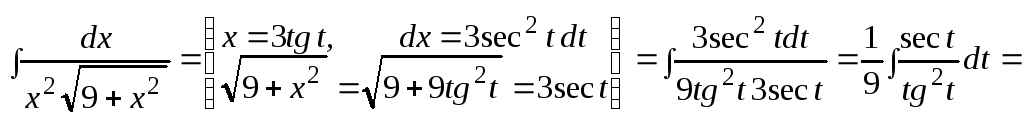
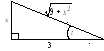6) .

Пусть , тогда, .

Пример 4.

, ,

.

.
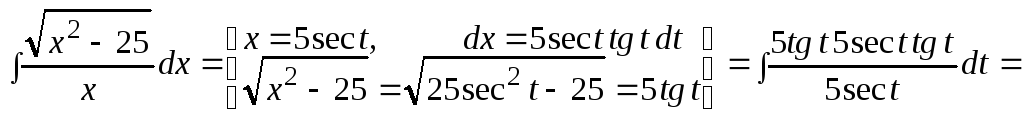
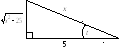