3.6.2. Вычисление длин дуг плоских кривых

Литература: [3], гл. XII, § 3

[5], Ч.2, гл. 10, § 10.5

Если кривая y = f (x) на отрезке [a, b] является гладкой (т.е. производная ─ непрерывная функция), то длина дуги этой кривой, заключенной между точками с абсциссами x = a и x = b, вычисляется по формуле

.

В том случае, когда кривая задана уравнениями в параметрической форме (─ непрерывно-дифференцируемые функции), длина дуги кривой, соответствующей монотонному изменению параметраt от α до β, вычисляется по формуле

.

Если, наконец, кривая задана уравнением в полярных координатах , то длина дуги кривой при изменении полярного углаотдо, находится по формуле

.

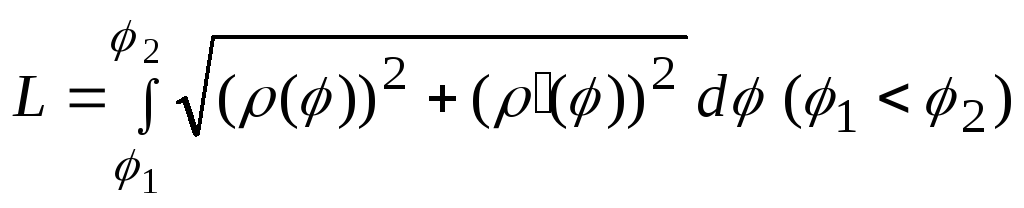Примеры. Найти длину дуги:

1) цепной линии от x = 0 до x = 2;

2) астроиды ;

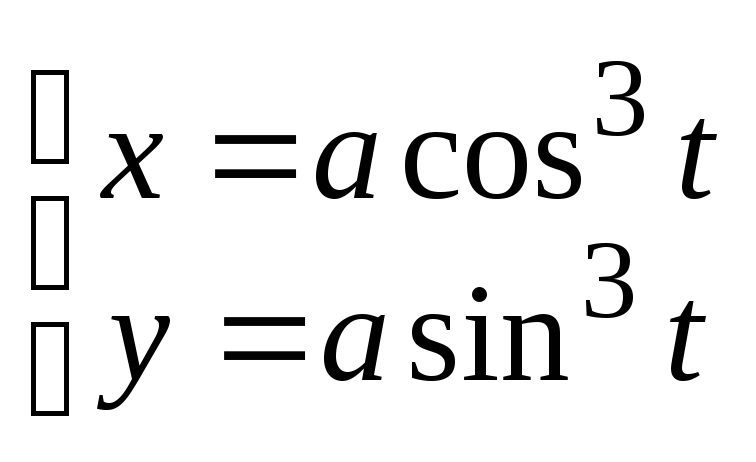3) кардиоиды .

Решение. 1) Дифференцируя, получаем 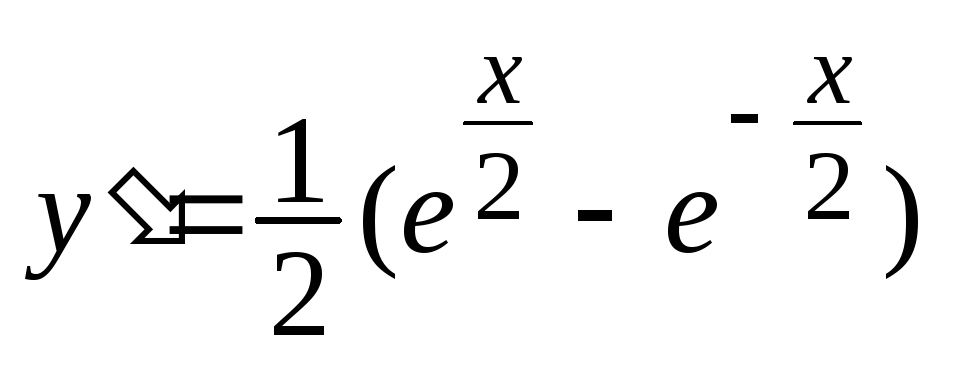, тогда

.

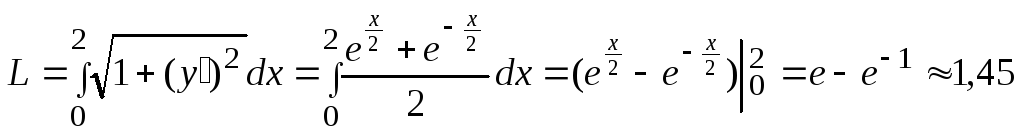2) В силу симметрии астроиды относительно координатных осей достаточно найти длину одной четверти всей кривой и результат умножить на 4. При этом параметр t будет изменяться от 0 до .

Находими:

, .

Тогда

.

Получаем

.

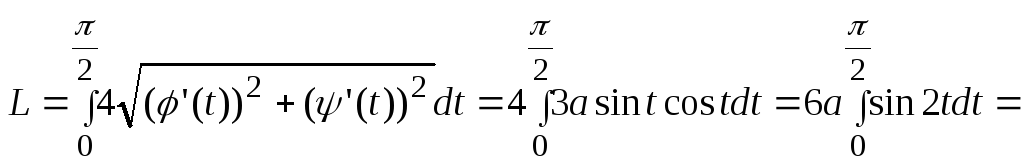
3) Так как кардиоида симметрична относительно полярной оси, то вычислим длину половины ее дуги (полярный угол φ изменяется от 0 до π), а затем умножим на 2. Найдем . Тогда

.

Теперь находим

.

3.6.3. Вычисление объемов тел вращения

Литература: [3], гл. XII, §§ 4, 5

[5], Ч.2, гл. 10, § 10.4

Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной непрерывной кривой y = f (x), осью абсцисс и двумя прямыми x = a, x = b (a < b), находится по формуле

.

Аналогично, объем тела вращения вокруг оси Oy криволинейной трапеции, ограниченной непрерывной кривой x = g (y), осью ординат и двумя прямыми y = c и y = d, вычисляется по формуле

.

Если кривая задана параметрическими уравнениями , то формулы для вычисления объема тела вращения принимают вид

и .

Пример. Вычислить объем тела, полученного вращением эллипса : 1) вокруг оси Ox, 2) вокруг оси Oy.

Решение.

1) ;

2) .

3.6.4. Вычисление площадей поверхностей тел вращения

Литература: [3], гл. XII, § 6

[5], Ч.2, гл. 10, § 10.6

Площадь поверхности, образованной вращением вокруг оси Ox дуги гладкой кривой y = f (x) между точками с абсциссами x = a и x = b, вычисляется по формуле

.

Если кривая задана параметрическими уравнениями , то формула для вычисления площади поверхности вращения принимает вид

.

Пример. Найти площадь поверхности вращения вокруг оси Ox одной арки циклоиды

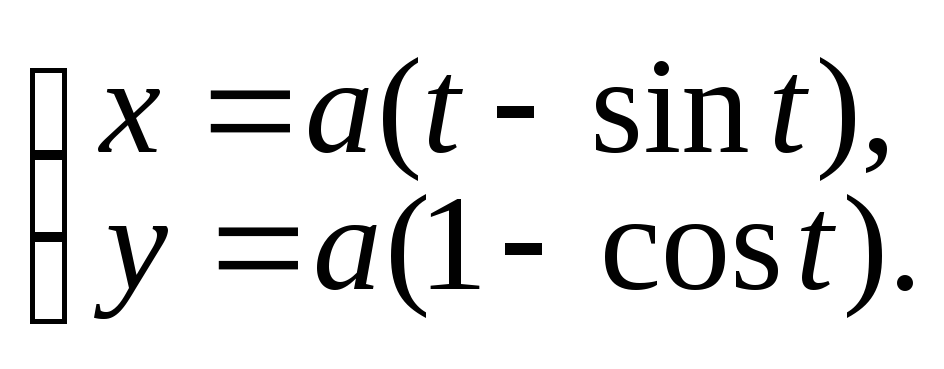
Находим . Подставляем полученные выражения в формулу дляи, учитывая, что параметрt изменяется от 0 до 2π, получим:

.

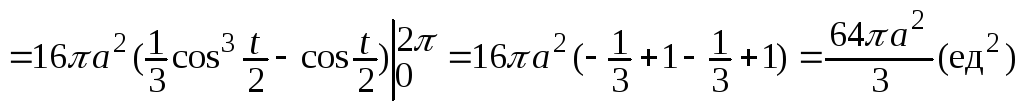4. Несобственные интегралы

Литература: [3], гл. XI, § 7

При определении определенного интеграла предполагалось, что: 1) отрезок интегрирования [a, b] конечен;

2) подынтегральная функция f (x) определена и ограничена на [a, b].

Если нарушается хотя бы одно из этих условий, то интеграл называется несобственным. При этом, если нарушено только первое условие, то говорят о несобственном интеграле первого рода (или интеграле с бесконечными пределами интегрирования). Если нарушено только второе условие, т. е. подынтегральная функция имеет бесконечный разрыв на отрезке [a, b], то говорят о несобственном интеграле второго рода (или интеграле от неограниченной функции).