3.2. Основные свойства определенного интеграла
1.
.
2.
.
3.
.
4. Постоянный множитель можно вынести за знак интеграла:
,
.
5. Определенный интеграл от алгебраической суммы конечного числа функций равен сумме определенных интегралов от этих функций:
.
6. Отрезок интегрирования можно разбить на части:
.
Причем это свойство справедливо для любого расположения точек a, b и c на числовой оси.
7.
Если f1(x)
и f2(x)
интегрируемы на [a;
b]
и для всех x
на [a;
b]
выполняется неравенство
иa
< b,
то
,
т.е. неравенство можно почленно интегрировать.
В частности, если
,
то
.
8.
.
9.
Если f
(x)
непрерывна на [a;
b],
то
,
где
,
и
.
10.
Теорема о
среднем.
Если f
(x)
непрерывна на [a;
b],
то существует точка
такая, что
.
3.3. Вычисление определенного интеграла. Формула Ньтона-Лейбница
Литература: [3], гл. XI, § 2
[5], Ч.2, гл. 10, § 10.1
Пусть функция f
(x)
интегрируема на [a;
b].
Тогда для любого
она будет интегрируемой и на отрезке
[a,
x].
Заменим верхний предел b
определенного интеграла
переменнойx,
получим выражение
,
которое, очевидно, является функцией
отx.
Обозначим эту функцию через
.
Здесь переменную интегрирования мы
обозначим черезt,
чтобы не путать ее с верхним пределом
интегрирования x.
Функция Ф(x) обладает следующими свойствами:
1) если функция f (t) непрерывна на [a,b], то Ф(x) также непрерывна на этом промежутке;
2) если функция f (t) непрерывна в точке t = x, то в этой точке функция Ф(x) имеет производную, равную f (x), т.е.
.
Из последнего
равенства следует, что функция Ф(x)
является первообразной для f
(x)
на [a,
b]
. Отсюда вытекает очень важное утверждение:
всякая непрерывная на отрезке [a,
b]
функция имеет на том отрезке первообразную.
Если F (x)
другая первообразная для f
(x),
т.е.
,
то
.
Формула Ньютона-Лейбница. Определенный интеграл от непрерывной функции равен приращению какой-либо первообразной на промежутке интегрирования:
.
Здесь F (x) – любая первообразная для f (x) на [a, b].
Из формулы Ньютона-Лейбница и второго свойства функции Ф(x) следует, что все методы интегрирования для неопределенного интеграла справедливы для определенного интеграла.
Пример.
Вычислить интегралы: 1)
;
2)
.
Решение.
1)
.
2)
.
3.4. Замена переменной в определенном интеграле
Литература: [5], Ч.2, гл. 10, § 10.2
Рассмотрим
,
гдеf
(x)
непрерывна на [a,
b].
Введем новую переменную интегрирования
t,
связанную с переменной x
соотношением x=φ(t),
где
,
а
.
Функция φ (t) должна быть непрерывно-дифференцируемой. Кроме того, φ(α)=a, φ(β)=b, тогда имеет место формула
.
Следует отметить, что при вычислении определенного интеграла уже нет необходимости возвращаться к старой переменной интегрирования, т.к. пределы интегрирования изменились в соответствии с подстановкой.
Примеры.
Вычислить интегралы 1) 
;
2) 
.
Решение.
1. Введем новую
переменную интегрирования, полагая
.
Отсюда находим:
,
.
Вычислим новые пределы интегрирования:
при
имеем
,
при
получаем
.
Следовательно,
.
2. Положим
,
тогда
.
Находим новые пределы интегрирования:
при
получаем
,
,
.
При
получаем
,
,
.
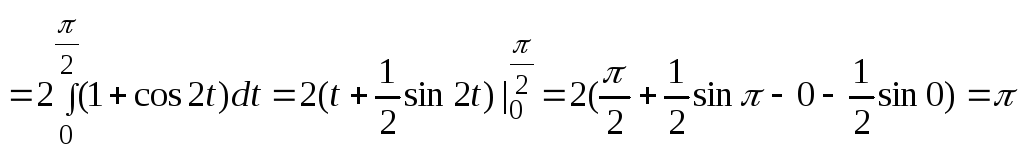
3.5. Интегрирование по частям
Литература: [5], Ч.2, гл. 10, § 10.2
Если функции u(x) и v(x) непрерывно-дифференцируемы на [a, b], то имеет место формула интегрирования по частям:
.
Примеры.
Вычислить интегралы: 1)
;
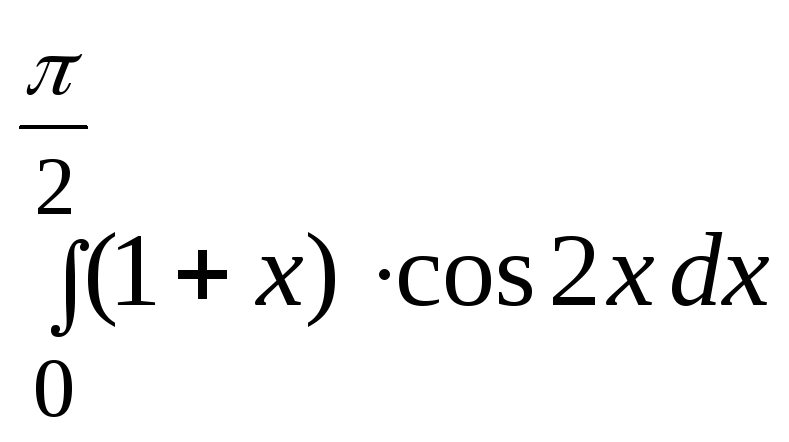2)
.
Решение.
1)
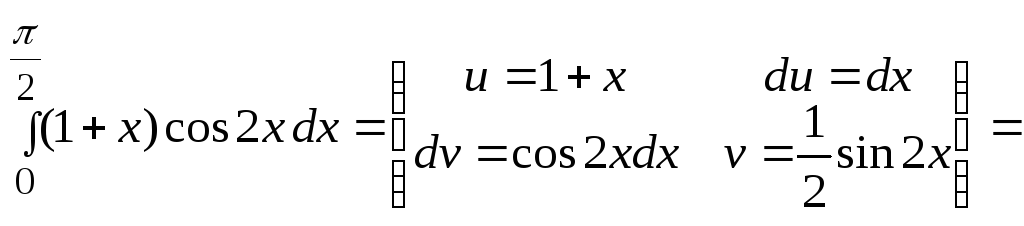
2)
Отметим очень важные для дальнейшего утверждения:
1)
если функция f
(x)
четная, то 
;
2)
если функция f
(x)
нечетная, то
;
3)
если f (x)
периодическая с периодом T,
то
.
3.6. Геометрические приложения определенного интеграла
3.6.1. Вычисление площадей плоских фигур
Литература: [5], Ч.2, гл. 10, § 10.3
Из геометрического
смысла определенного интеграла следует,
что если f
(x)
≥
0 для всех
,
то площадь криволинейной трапеции
ограниченной графиком функцииy
=
f
(x),
прямыми x=a,
x=b
и осью Ox,
выражается формулой
(рис. 3.2, а).
Если же f
(x)
≤
0 для всех
,
то
и, следовательно, в этом случае
(рис. 3.2, б).
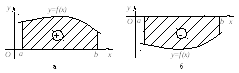
Рис. 3.2
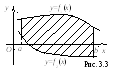
Если фигура
ограничена графиками функций y
=
f1
(x)
и y
=
f2
(x)
таких, что
f1
(x)
≥ f2
(x)
для всех
(рис. 3.3), то
.
Пример 1. Вычислить площадь фигуры, ограниченной линиями y=x и y=2−x2.
Решение. Найдем точки пересечения и построим заданные линии.
,
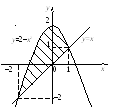
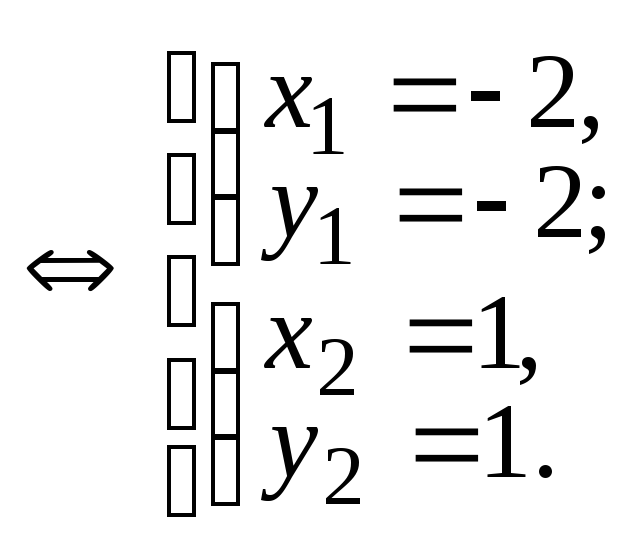т.е. a=–2,
b=1.
Тогда
.
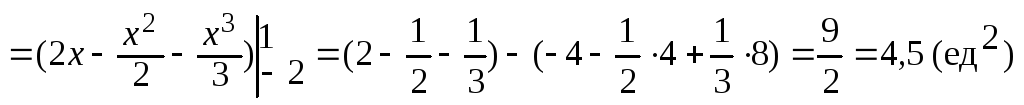Замечание. Часто бывает удобным использовать для вычисления площадей фигур формулы, в которых интегрирование ведется по переменной y, при этом x считается функцией от y, т.е.
и
.
Пример 2. Вычислить площадь, ограниченную линиями y2=2x+1 и y=x−1.
Р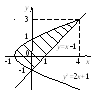
ешение.
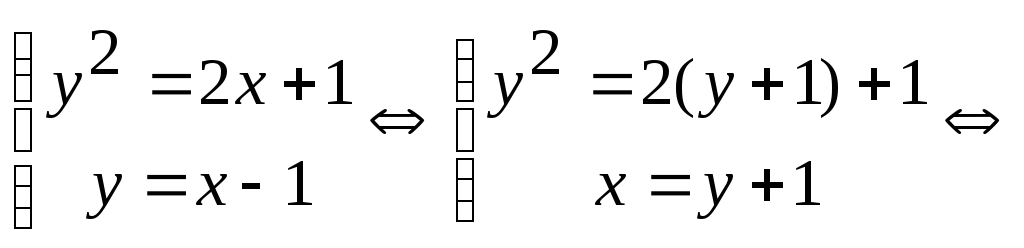
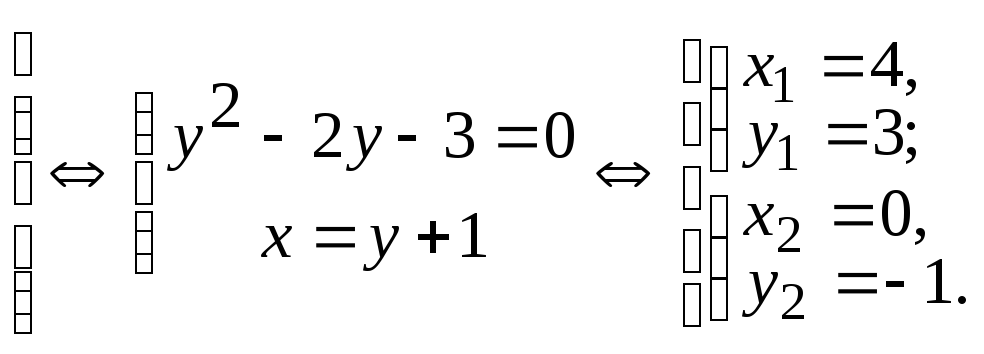
Площадь фигуры равна:
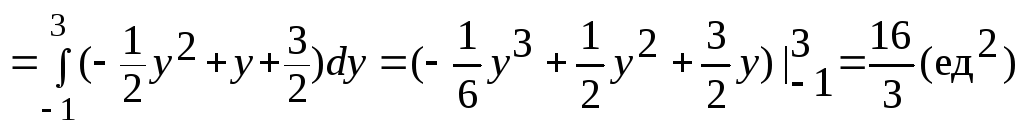
Если кривая,
ограничивающая сверху криволинейную
трапецию, задана в параметрическом виде
,
где
,
то
.
Пример 3.
Вычислить площадь фигуры, ограниченной
эллипсом
,
,
где 0 ≤ t
≤ 2π.
Р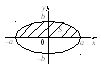
ешение.
В силу симметрии эллипса
Площадь криволинейного
сектора, ограниченного кривой
и двумя полярными радиусами
и
(
),
вычисляется по формуле
.
П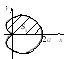
ример.
Вычислить площадь фигуры, ограниченной
кардиоидой
Решение.
