1.7. Производная функции, заданной неявно. Производная степенно-показательной функции. Производная функции, заданной параметрически

Литература: [5], Ч.1, гл. 5, § 5.2

Функция ,неявно задана уравнением , если для всехвыполняется тождество. Для нахождения производной функцииследует имеющееся тождество продифференцировать пох, учитывая, что , а затем полученное уравнение разрешить относительно

Пример 1. Найти производную функции , заданной неявно уравнением.

Решение. Дифференцируем по х обе части равенства, рассматривая у как функцию от х: , откуда

Степенно-показательной называется функция, у которой и основание и показатель степени являются функциями от х, т.е. функция вида . Например,,,.

Прологарифмируем равенство :,. Дифференцируем полученное равенство пох: . Откуда. Подставив, получим формулу для нахождения производной степенно-показательной функции.

Пример 2. Найти производную этой функции .

Решение. ,, откуда.

Прием, нахождения производной, при котором вначале логарифмируется заданная функция, а затем дифференцируется полученное выражение, называется логарифмическим дифференцированием. Он широко применяется при дифференцировании громоздких выражений, состоящих из нескольких сомножителей и делителей.

Если функция заданапараметрически , то ее производнаяпо переменнойвычисляется по формуле.

Пример 3. Найти , если функциязадана параметрически

Решение. Вначале находим производные от ипо переменной:,. Тогда производная отпоравна

1.8. Производные высших порядков

Литература: [5], Ч.1, гл. 5, § 5.4

Производной второго порядка (второй производной) функции y = f (x) называется производная от ее производной.

Вторая производная обозначается или.

Если ─ закон прямолинейного движения точки, то вторая производная пути по времени есть ускорение этого движения. В этом заключаетсямеханический смысл второй производной.

Аналогично, производной третьего порядка функции y = f (x) называется производная от производной второго порядка: . Вообще, производнаяn-го порядка от функции y = f (x) называется производная от производной (n-1)-го порядка: .

Производные высших порядков (вторая, третья и т.д.) вычисляются последовательным дифференцированием данной функции.

Пример 1.. Найти , если.

Решение. Применяя последовательно правила дифференцирования суммы и произведения, а также правило дифференцирования сложной функции, найдем первую производную заданной функции:

.

Дифференцируя первую производную, найдем вторую производную заданной функции: .

Если функция заданапараметрически , то производные,, … вычисляются по формулам:

, ,и т.д.

Производную второго порядка функции, заданной параметрически, можно также вычислить по формуле: .

Пример 2. Найти и, если функция задана параметрически

Решение. Имеем

,

.

Покажем на примере способ нахождения производных высших порядков от функций, заданных неявно.

Пример 3. Найти вторую производную функции , заданной неявно уравнением.

Решение. Дифференцируя уравнение поx, получим:

.

Продифференцировав равенство поx и разрешив его относительно , получим:

.

Подставив уже найденное значение в выражение для второй производной, выразимчерезx и y:

.
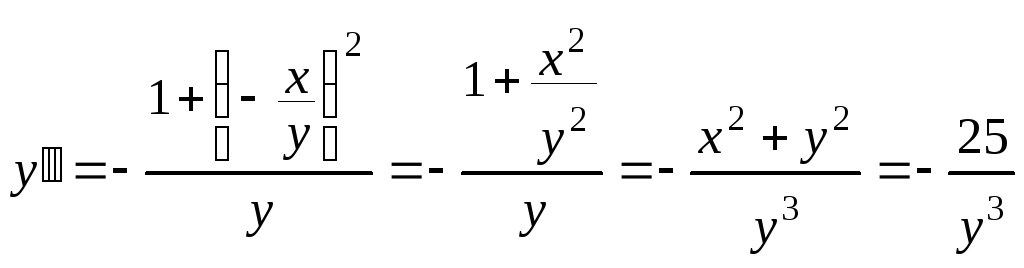