2.4. Метод интегрирования по частям

Литература: [3], гл. X, § 6

[5], Ч.2, гл. 9, § 9.3

Если u=u(x) и v=v(x) ─ непрерывно дифференцируемые функции, то имеет место формула интегрирования по частям

,

которая позволяет вычисление интеграла свести к вычислению более простого интеграла, если удачно выбрать функциюu(х). Чаще всего это бывает в тех случаях, когда подынтегральная функция представляет собой произведение разных элементарных функций: степенной и показательной, степенной и тригонометрической, показательной и тригонометрической и т.д.

Отметим наиболее часто встречающиеся варианты функций.

Если подынтегральная функция представляет собой произведение степенной функции на тригонометрическую или показательную функции, то.

Если подынтегральная функция равна произведению степенной функции на логарифмическую или обратную тригонометрическую функцию, то запринимают последние функции, а степенную функцию относят к.

При интегрировании функций вида ,безразлично, какую из функций принимать заu. Интегрирование по частям применяется дважды (и оба раза за u принимают одну и ту же функцию), в результате чего получается уравнение относительно искомого интеграла, решив которое, находим этот интеграл.

Рассмотрим несколько примеров на применение формулы интегрирования по частям.

Пример 1.

.

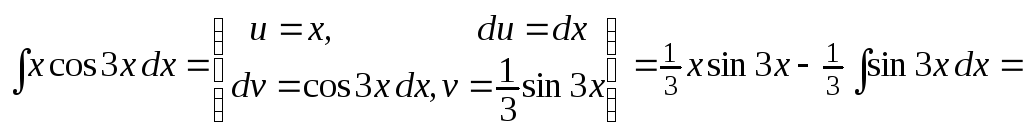
Пример 2.

.

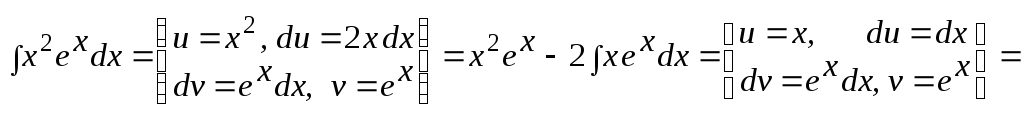
Пример 3.

Пример 4.

.

Пример 5.

,

откуда .

Итак, .

2.5. Интегрирование некоторых функций, содержащих квадратный трехчлен

Литература: [3], гл. X, § 5

[5], Ч.2, гл. 9, § 9.4

_{Прежде всего необходимо уметь выделять из квадратного трехчлена полный квадрат:}

.

Рассмотрим интеграл . Выделив из квадратного трехчлена полный квадрат и заменив, получим табличный интеграл вида(см. формулы 11, 12).

Пример 1.

.

Аналогично находится интеграл .

Пример 2.

.

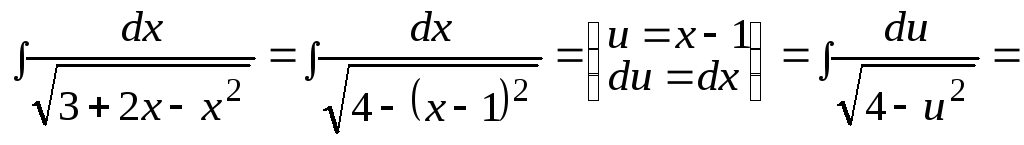
Здесь выделение полного квадрата проведено следующим образом:

.

Рассмотрим интеграл , где. Прежде всего в числителе подынтегральной функции следует выделить производную квадратного трехчлена, далее дробь представить в виде суммы двух дробей, интеграл заменить суммой интегралов, каждый из которых легко сводится к табличному.

Пример 3.

.

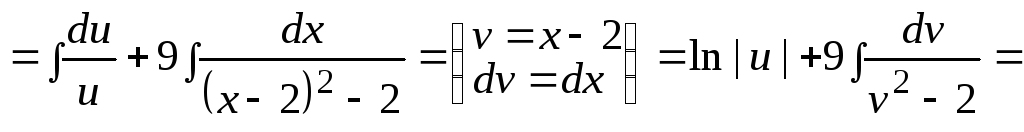
Аналогично можно найти интеграл .

Пример 4.

.

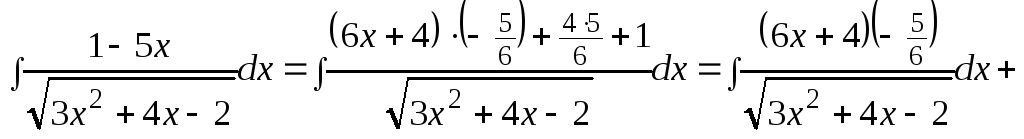
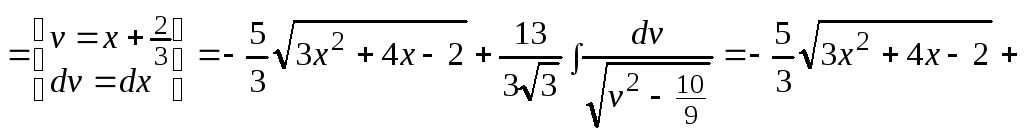
2.6. Интегрирование дробно-рациональных функций

Литература: [3], гл. VII, §§ 6-8; гл. X, §§ 7-9

[5], Ч.2, гл. 9, § 9.5

Многочленом n-й степени относительно переменной x называется функция вида , где .

Корнем многочлена называется такое значениеx, при котором многочлен обращается в нуль, т.е. которое является корнем уравнения . Например, корень многочленаесть , т.к. .

Число х₀ называется k-кратным корнем многочлена , если этот многочлен можно представить в виде, где.

Теорема. Любой многочлен с действительными коэффициентами может быть представлен единственным образом в виде произведения линейных и квадратичных множителей (с отрицательным дискриминантом) с действительными коэффициентами:

,

где ─ действительный корень многочлена кратностиk_i , для дискриминант.

Дробно-рациональной функцией или просто рациональной дробью называется функция, равная отношению многочленов:

,

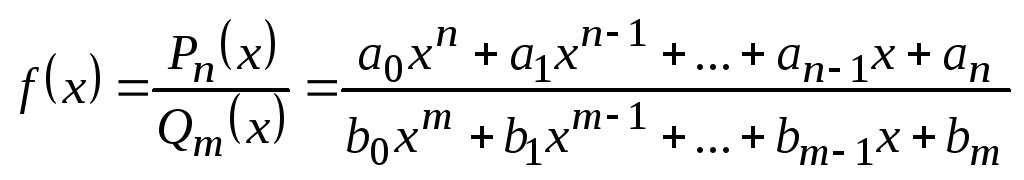где .

Если , то рациональная дробь называется правильной, если , то дробь называется неправильной. Например,

─правильная рациональная дробь ();

─неправильная дробь ();

─неправильная дробь ().

Неправильную рациональную дробь всегда можно представить в виде суммы целой части (многочлена) и правильной рациональной дроби.

Например, .

Б

_ x³-2x²-5x-1 │x²+x-5

x³+ x²-5x │x-3

_-3x²-0x-1

-3x²-3x+15

3x-16

олее общим методом выделения целой части является деление многочлен на многочлен в столбик.

Например,

Таким образом, .

Поскольку интегрирование целой части (многочлена) не представляет труда, остаётся рассмотреть метод интегрирования правильных рациональных дробей.

Простейшими дробями называются рациональные дроби следующих четырёх типов:

I. , где.

II. , где.

III. , где,А и В не равны нулю одновременно.

IV. , где,А и В не равны нулю одновременно,

Интегрирование дробей типа І и ІІ особого труда не составляет:

;

.

Интегрирование дроби типа III рассмотрено в п. 2.5. Подобным образом можно проинтегрировать дробь типа IV.

Теорема. Всякая правильная рациональная дробь может быть представлена единственным образом в виде суммы некоторого количества простейших рациональных дробей типов I − IV, а именно: в разложении дроби каждому множителю видазнаменателясоответствует суммаk простейших дробей I − II типов:

,

а каждому множителю вида , где, соответствует суммаs простейших дробей III − IV типов:

.

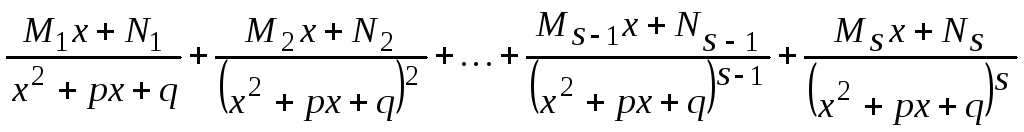Например, согласно этой теореме приведённую ниже дробь можно следующим образом разложить на сумму простейших дробей:

.

Коэффициенты A, B, C, D, M₁, N₁, M₂, N₂ следует подбирать так, чтобы сумма всех дробей, стоящих справа, была равна данной дроби.

Правило. Чтобы разложить правильную дробь на сумму простейших, необходимо:

1) знаменатель Q_m(x) дроби разложить на линейные и квадратичные (с отрицательным дискриминантом) множители;

2) составить формулу разложения данной дроби на сумму простейших дробей с неопределёнными коэффициентами;

3) привести эту сумму к наименьшему общему знаменателю (он равен знаменателю данной дроби) и приравнять числители;

4) полученное равенство использовать для составления системы уравнений относительно неопределённых коэффициентов, количество уравнений системы должно быть равно числу неопределённых коэффициентов;

5) решить составленную систему уравнений и подставить найденные коэффициенты в формулу разложения.

Для составления системы уравнений относительно неопределённых коэффициентов можно использовать следующие утверждения:

1) два многочлена равны тогда, и только тогда, когда равны их коэффициенты при одинаковых степенях x;

2) два многочлена равны тогда, и только тогда, когда их числовые значения равны при любом значении x (в том числе при значениях x, равных корням знаменателя).

Пример. Найти интеграл .

Решение. Подынтегральная функция представляет собой неправильную рациональную дробь, т.к. степени многочленов, стоящих в числителе и знаменателе, равны (m=n=3). Поэтому, прежде всего надо выделить целую часть дроби.

Итак, .

Полученную правильную рациональную дробь разложим на сумму простейших дробей. Для этого разложим на простейшие множители знаменатель . Тогда разложение дроби имеет вид

.

Коэффициенты A, B, C надо подобрать так, чтобы числитель последней дроби был равен числителю данной дроби (их знаменатели равны):

Составим систему уравнений (три уравнения с тремя неизвестными A, B, C), подставляя в равенство числителей корни знаменателя:

.

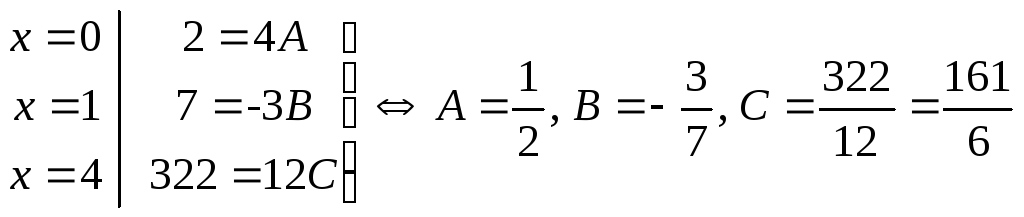Итак, .

.