Скобцовы Моделирование и тестирование

1.МОДЕЛИ ЦИФРОВЫХ УСТРОЙСТВ

1.1Уровни и области моделирования

При автоматизации проектирования и диагностирования дискретных устройств (ДУ) широкое применение находят системы моделирования.

Для представления устройств они требуют соответствующих математических моделей. При проектировании ДУ следует различать модели устройств и их спецификации [39]. Спецификации описывают устройство в терминах получаемых результатов проектирования, таких как схемы, временные диаграммы и т.п. Модели используются в процедурах проектирования устройств при моделировании в данной области (domain),

на данном уровне представления для проверки соответствия заданным спецификациям. Они также применяются для установления соответствия между различными уровнями и областями проектирования.

Физическая область

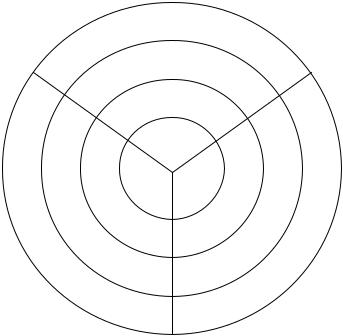
Рис.1.1 Уровни абстракции

13

Для каждой из областей – физической, структурной и поведенческой различают различные уровни: схемный, логический, языков регистровых передач (ЯРП) и системный. При этом в поведенческой области дается функциональное представление ДУ, в структурной области описываются блоки архитектуры ДУ, физическая область отражает реальный кристалл

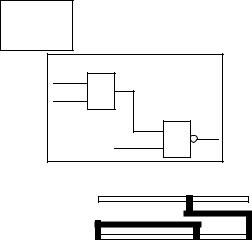
(chip). Например, для логического уровня эти три области показаны на

рис.1.2.

Физический

уровень

b c

Рис.1.2 Области представления схемы на логическом уровне

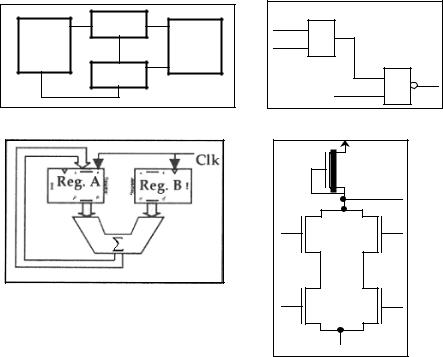
С другой стороны на рис.1.3 показаны различные уровни для структурной области. В табл.1.1 представлены различные уровни проектирования ДУ для каждой области. Следует отметить, что ДУ на одном и том же уровне в данной области может быть описано различными способами. Например, ДУ на логическом уровне в поведенческой области может быть описано с помощью булевых выражений, таблиц, языка программирования, языка описания аппаратуры.

14

элементов или логическом моделировании ДУ. При этом, как правило,

элементы, составляющие ДУ, описываются с помощью логических уравнений (булевых функций), которые отражают логику их функционирования. Кроме этого исследуются функциональные модели ДУ на уровне регистровых передач.

Объектом наших исследований являются ДУ, которые делятся на два класса [1,2]: комбинационные и последовательностные устройства. ДУ называется комбинационным, или ДУ без памяти, если значения его выходных сигналов однозначно определяются только значениями входных сигналов. Последовательностным, или ДУ с памятью, называется устройство, у которого значения выходных сигналов в данный момент времени зависят от значений входных сигналов в текущий момент и от внутреннего состояния объекта в предыдущий момент времени,

определяемого значениями сигналов на линиях обратных связей. При построении моделей ДУ мы рассмотрим три подхода: функциональный,

структурный и представление ДУ языками описания аппаратуры (hardware

design languages - HDL).

1.2 Функциональные модели

Суть функционального подхода заключается в абстрагировании от внутренней организации устройства и рассмотрении только его логики функционирования. Как правило, под ДУ подразумеваются устройства,

перерабатывающие двоичную информацию.

1.2.1 Модели комбинационных схем

В качестве функциональной модели комбинационных устройств,

чаще всего, используют систему булевых функций:

z1 = f1(x1,...xn )

…

zm = fm (x1,...xn ) ,

16

где X=(x1,...,xn) - входные, Z=(z1,...,zm) - выходные переменные,

принимающие двоичные значения B2={0,1}. Данная система булевых функций описывает комбинационное ДУ, которое имеет n входов, m

выходов и представлено на рис. 1.4.

Рис.1.4 Комбинационное ДУ

Здесь каждая булева функция fi (x1,..., xn ) - отображение B2n → B2 .

Простейшим способом представления булевой функции является таблица истинности. Например, в табл.1.2 приведена таблица истинности для булевой функции трех переменных.

Кроме этих таблиц часто используются также табличные модели в виде так называемых «примитивных» (простых) кубов. Эти кубы в сжатом виде фактически представляют ту же самую информацию. Один

«примитивный» куб объединяет несколько «соседних» строк таблицы истинности, на которых булева функция принимает одно и тоже значение.

Под «соседними» здесь понимаются строки, отличающиеся значением одного (или более) бита. В отличие от таблиц истинности такие кубы используют не двоичный алфавит B2={0,1}, а троичный алфавит

E3={0,1,x}, где символ х представляет неопределенное значение (0 или 1)

переменной. В табл.1.3 представлена табличная модель в виде

«примитивных» кубов той же булевой функции (табл.1.2).

17

В табл. 1.3 первая строка («примитивный» куб – х110) объединяет третью

(0100) и седьмую (1100) строки исходной таблицы истинности. Отметим,

что третья стока (куб х0х1) объединяет четыре строки таблицы истинности, имеющих всевозможные значения переменных х1 и х3 и одно и тоже значение булевой функции f=1. Фактически, «примитивный» куб соответствует простой импликанте [40].

1.2.2 Модели последовательностных схем

В качестве функциональной модели последовательностных устройств используется абстрактный конечный автомат, являющийся совокупностью пяти объектов A=(Y,X,Z,δ,λ), где Y, X, Z – конечные множества состояний, входных и выходных сигналов соответственно;

δ:Y×X→Y - функция переходов, определяющая следующее состояние автомата; λ:Y×X→Z - функция выхода, определяющая выходной сигнал.

Различают два типа автомата:

автомат Мили Y (t + 1) = δ (Y (t), X (t))

Z(t + 1) = λ (Y (t), X (t)) ;

и автомат Мура Y (t + 1) = δ (Y (t), X (t))

18

Z(t +1) = λ (Y (t)) .

Например, табл. 1.4 представляет конечный автомат Мили с одним входом – х, одним выходом – z и четырьмя состояниями. Здесь на пересечении строки (текущего состояния) и столбца (входного сигнала)

приводятся следующее состояние и выходной сигнал автомата.

Таблица 1.4

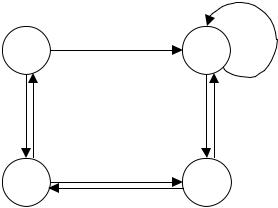
Кроме приведенной табличной формы автомат также часто представляется графом переходов и выходов. Для примера на рис.1.5

показан граф переходов –выходов автомата, представленного табл.1.4.

Рис.1.5 Граф переходов – выходов автомата табл.1.4

Следует отметить, что в этой форме представления неявно предполагается, что функционирование автомата рассматривается в

19

дискретном времени, принимающем целые неотрицательные значения t=0,1,2... Такие автоматы называются синхронными.

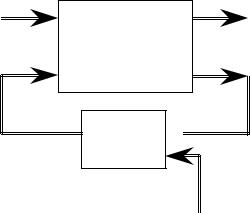
Синхронное последовательностное ДУ имеет каноническую форму представления, приведенную на рис.1.6. Эта автоматная модель позволяет представить последовательностное устройство в виде комбинационного блока и блока памяти, которые соединены линиями обратной связи

Y=(y1,...,yk).

F/Fs

Синхроимпульс

CLOCK

Рис.1.6 Модель схемы с памятью

Здесь каждое состояние в таблице автомата соответствует комбинации переменных состояния - y. Синхронизация неявно реализуется в виде дополнительного входа – clock. Таким образом события (изменение состояния и выходного сигнала ) инициируются импульсами на входе синхронизации. Состояние схемы запоминается в синхронизируемых триггерах (flip-flop - FF) и изменяется при поступлении импульсов на соответствующий вход. На рис.1.7 представлены три используемые на практике типа синхронизируемых триггеров: JK-триггер, Т-триггер и D-

триггер (задержка). В общем случае синхронные ДУ могут иметь несколько входов синхронизации.

20