Teoriya avtomatichnogo keruvannya

У системах із зоною нечутливості або з сухим тертям з'являється зона застою, а на фазовій площині замість особливої точки — особлива лінія. Фазовий портрет, що відповідає неасимптотично стійкій си стемі, зображено на рис. 8.7, е.

Отже, динамічні процеси у нелінійних системах суттєво відрізняються від процесів у лінійних: значно ширше трактується поняття про стійкість, у тій самій системі залежно від початкових відхилень можуть спостерігатися якісно різні перехідні процеси тощо. В цілому за своїми властивостями нелінійні системи значно багатші за лінійні.

8.5

АослідЖення нелінійних систем методом фазової площини

Метод фазової площини належить до точних методів дослідження нелінійних систем. Найповніше цей метод розроблено для систем другого порядку. Сукупність

фазових траєкторій (фазовий портрет), що відповідають різним початковим положенням зображуючої точки, як указувалося раніше, дає повне уявлення про динаміку нелінійної системи. Тому дослідження нелінійних систем методом фазової площини по суті зводиться до побудови фазового портрета й аналізу за його допомогою динамічних режимів системи.

Як зазначалося раніше, рівняння фазової траєкторії у = /(.х) є розв'язком рівняння (8.31) першого порядку. Спосіб розв'язування цього рівняння залежить від типу характеристики нелінійної ланки. Загальним методом розв'язування є чисельне інтегрування за допомогою ЕОМ. Для кусково-лінійних нелінійних характеристик у деяких випадках розв'язок рівняння (8.31) може бути знайдено аналітично для окремих лінійних ділянок нелінійної характеристики. Кожна лінійна ділянка нелінійної характеристики описується своїм рівнянням вигляду (8.31) і, отже, для кожної ділянки отримуємо різні рівняння фазових траєкторій. ГІри цьому на фазовому портреті з'являться так звані лінії перемикання, що розділяють фазову площину на зони з різними фазовими траєкторіями.

410

8.5. Дослідження нелінійних систем

ч.ір.п геристик на рис 8.1, а, б, д рівняння ліній перемикання мають иіп 'під х, - с\ х2 = -с; для характеристики на рис. 8.1, в — х = 0;

перемикання: х, = с при у > 0 і х2 = -с при у < 0.

Якщо на фазовій площині є лінії перемикання, то при розрахуй- * \ фа ювих траєкторій початкові значення х і у для кожної ділянки ми міачаються через їх кінцеві значення на попередній ділянці.

Фазові траєкторії можна побудувати й не розв'язуючи рівняння

іЧ), якщо скористатися методом ізоклін.

Іюкліни (лінії однакового нахилу) — це лінії, вздовж яких похідна

./1 г/\ має стале значення. Через те, що сіу/сіх - С - сопзі:, ізокліна « і.мювить геометричне місце точок з однаковим кутом нахилу дотичппч до (разових траєкторій, що проходять через ці точки. Кут а нахи-

І Іс рівняння є алгебричним. Надаючи Срізних значень від -<*> до

,побудуємо сім'ю ізоклін, використавши яку, легко дістати фазові

ірас к юрії за будь-яких початкових умов (будь-якому початковому іюііоженні зображуючої точки).

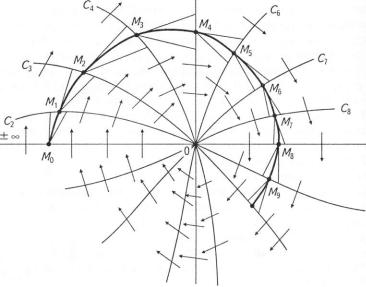
( ім'ю ізоклін наведено на рис 8.8. Стрілками на кожній ізокліні їмч азано кути нахилу дотичних до фазових траєкторій. Очевидно, мю вісь абсцис (у = 0) відповідає ізокліні С = ±°о і куту а = ±п/2. Для ім п»удови фазової траєкторії слід задати початкові умови (вихідні ко-

"Р іипаги зображуючої точки). Потім через точку М0 провести дві ним Нахил першої має збігатися з нахилом стрілки на ізокліні С{, мру і о і з нахилом, що відповідає суміжній ізокліні С2 . Вважаємо,

ми» і очка Л/, лежить майже посередині відрізка, що відтинається на мої міні С2 лініями, проведеними з точки М0 . Аналогічно відшуку- ІОІІ.І я точки М 2 , М 3 , . . . і будується фазова траєкторія.

іл (разовим портретом нелінійної системи можна зробити не п м і и якісну оцінку її динаміки (стійка система чи ні, коливальний

411

Рис. 8.8

або аперіодичний перехідний процес, чи є автоколивання тощо), а й визначити кількісні показники якості перехідних процесів. На фазовій площині час у явному вигляді відсутній, але наближено швидкодію системи можна оцінити, виходячи з величини у - сіх/сії, яка становить швидкість зміни вихідної змінної.Час переміщення зображуючої точки з одного положення Мх в інше, досить близьке, М2 можна наближено знайти за формулою

А/ = Ах/усер,

де Ах і усср визначаються для окремих ділянок фазової траєкторії так, як показано на рис. 8.9.

За фазовим портретом на рис 8.9 можна знайти також величину перерегулювання а (%):

а = ^ 1 0 0 ,

ОА

412

8.5.Дослідження нелінійних систем

~методом фазової площини

і• • ОЛ початкове (максимальне) відхилення вихідної величини від

і і існого значення; ОБ — відхилення через час, що дорівнює полоши 11 періоду коливань.

'>а граничним циклом на фазовому портреті можна визначити амп мі іуду та частоту автоколивань. Якщо реальний граничний цикл май ніжено замінити еквівалентним еліпсом з напівосями хт а х і утах ірис 8.10), то параметри автоколивань можна визначити за такими формулами:

амплітуда

Т= 2я/сой.

1 І П р и к л а д 8.2. Методом фазової площини виконати дослідження слідкувального електропривода, функціональну схему якого показано на рис. 8.4. Вважати, що вимірювальний, перетворювальний і підсилювальний елементи описуються однією нелінійною функцією ия = ф(е),де г 0[1Х - 0ВИХ; ия — напруга на якорі двигуна; електромагнітна стала

.двигуна Гя дорівнює нулю і люфта в редукторі немає.

Р о з в ' я з а н н я . Я к щ о прийняти, що Тя = 0, то передаточна функція двигуна

Дшд(/0 _ кл

(Р) ТмР+1'

413

де — коефіцієнт передачі двигуна; Тм — електромеханічна стала часу електропривода.

Редуктор, вхідною величиною якого є швидкість С0Д, а вихідною кут повороту 0ВПХ, описується передаточною функцією

Рис. 8.11

414

8.5. Дослідження нелінійних систем методом фазової площини

Результат розрахунку подано у вигляді фазової траєкторії на рис. 8.12. Ця траєкторія має вигляд спіралі, що стягується до початку координат. Отже, система стійка і перехідний процес має вигляд зату-

ш к и реального релейного елемента (рис. 8.1, є). У цьому разі стандартну програму розв'язування системи рівнянь слід доповнити умовами:

Ці умови записано з урахуванням рівнянь (8.7), я к щ о ск/сІЇ = - х, і г -- -х1. Розрахунок в и к о н а н о для тих самих умов, що й у попередньому випадку, крім того, п р и й н я т о Ь - 100 В, с - 0,25 рад.

Розраховану фазову траєкторію наведено па рис. 8.13. Фазовий портрет має стійкий граничний цикл, отже, усталеним режимом сис-

у.

^1 4

/12

-\6 /

4 15

Глава 8 НЕЛІНІЙНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ

8.6

Метод Ляпунова

Теореми першого методу Ляпунова сформульовані в гл. 4, п. 4.1 Вони надають можливість викорис товувати методи лінійної теорії для дослідження реальних неліиій

них систем. Природно, що цей висновок справедливий тільки для систем, що містять несуттєві нелінійності. Для систем із суттєвими нелінійностями перший метод Ляпунова застосовувати не можна.

Перш ніж сформулювати теореми другого (прямого) методу Ля пунова введемо такі поняття.

Функція У(х1, х2,..., хп) називається знсікосталою в деякій зоні, якщо вона зберігає один і той самий знак в усіх точках цієї зони най коло початку координат, за винятком деяких точок, в яких вона до рівнює нулю. Знакостала функція, що дорівнює нулю тільки в почаї ку координат, називається знаковизначеною (безумовно-додатною або безумовно-від'ємною). Функція називається знакозмінною, якщо вона в деякій зоні навколо початку координат може мати різні знаки Рівняння вільного руху системи подаються в нормальній формі

Коші

стійка.

Теоремі Ляпунова можна дати досить наочну геометричну інтерпретацію. Візьмемо, наприклад, знаковизначену додатну функцію

416

8.6.Метод Ляпунова

І(х, , х 2 , ... , хл )і надаватимемо їй сталі значення V = 0, С,, С2 ,..., що збільшуються. Кожному рівнянню У(х{, х2,..., хп) = Сі відповідає тмкнута поверхня у /7-вимірному просторі станів даної системи. По-

верхня, що відповідає значенню С/5 цілком перебуває всередині поверхні Сі + {, якщо Сі + { > С,. Ці поверхні зображено на рис. 8.14. Для наочності простір прийнято тривимірним. Якщо зображуюча точка в

Рис. 8.14

просторі станів рухається так, що переходить з поверхні, яка відповідає більшому Сі, на поверхню з меншим С,, тобто наближується до початку координат, то система стійка. Але якщо зображуюча точка рухається таким чином, то визначено-додатна функція Кзменшується з часом, тобто її повна похідна сіУ/сіі буде від'ємною. Отже, для стійкої системи функція У і її повна похідна мають протилежні знаки.

Дослідження стійкості методом Ляпунова проводять у такому порядку.

1. Записують рівняння вільного руху системи в нормальній формі Коші.

2. Вибирають функцію Ляпунова.

3. Визначають похідну с і У / с і і за формулою (8.38), в якій похідні (Іхк /<// замінюють функціями /к (х{, х 2 , ... , хп), тобто дістають похідну (!\ /(її як функцію координат системи і її параметрів.

4. Визначають межі зміни координат системи і її параметрів, у яких похідна сіУ/сіі залишається знаковизначеною, тобто знаходять умови стійкості.

Складність застосування прямого методу Ляпунова полягає в тому, що немає загальних рекомендацій щодо визначення функції Ляпунова. Для заданих у формі (8.37) нелінійних рівнянь системи можна вибрати кілька різних віріантів функції У, оскільки необхідною умовою є тільки знаковизначеність функції У і її похідної. За різних варіантів функції дотримують різні умови стійкості тієї самої системи. Теорема Ляпунова дає достатні умови стійкості, тобто при їх виконанні система обов'язково буде стійкою, але ці умови можуть не охоплювати всю зону стійкості системи. Невиконання умов теореми Ляпунова для вибраної функції У ще не доводить нестійкість системи, бо, власне кажучи, невідомо, чи є інші функції У, для яких умови теореми виконуються.

Для попередньо лінеаризованої нелінійної системи О.М. Ляпунов запропонував знаходити функцію У у вигляді квадратичної форми з невизначеннми коефіцієнтами:

к ,1 = І

Коефіцієнти ак, визначають з умови

де А — будь-яка стала величина. Для цього з виразу (8.39) знаходять частинні похідні с і У / с і х , а похідні сіх ] /сії беруть з лінеаризованих рівнянь руху вигляду (8.37). Ці похідні підставляють у формулу (8.40), прирівнюють коефіцієнти при однакових членах хкх, у лівій і правій частинах і дістають систему алгебричних рівнянь для визначення коефіцієнтів ак1.

Для нелінійних систем, що містять одну безінерційну нелінійність ф(в), А. І. Лур'є запропонував вибирати функцію У у вигляді

о

де В — квадратична форма координат системи; А — стале число.

•П р и к л а д 8.3. Визначити умови стійкості системи, структурну схему якої наведено на рис. 8.11 (див. приклад 8.2), за умови, що нелінійність Ф(Є)Є непарною однозначною.

418

8.6.Метод Ляпунова

Ро з в ' я з а н н я . Враховуючи, що є = -х2, запишемо рівняння (8.33), (8.34) у вигляді

Функцію Ляпунова візьмемо знаковизначеною додатною у формі Лур'є:

асимптотично стійка за таких обмежень на вигляд нелінійної характеристики Ф(Х2), які було прийнято при дослідженні стійкості:

1) характеристика має бути непарною, тобто при г = - х 2 Ф(Є) =

=- Ф ( * 2 ) ;

2)характеристика повинна розміщуватися в першому та третьому

Крім теореми про стійкість, О. М. Ляпунов сформулював теоре- му, що дає достатні умови нестійкості нелінійної системи. Якщо при иданих у вигляді (8.37) рівняннях системи похідна від якої-небудь функції Ляпунова К(х, , х 2 , х „ ) б у д е знаковизначеною, причому са- ма функція У в якій-небудь зоні, що примикає до початку коордипа і, матиме знак, однаковий зі знаком похідної, то система нестійка.

419