Teoriya avtomatichnogo keruvannya

Випадкова величина X, що змінюється в часі ї, становить випадковий процес. Інакше кажучи, випадковий процес — це функція часу, значення якої в кожний момент часу є випадковою величиною. Отже, випадковий процес Х(і) — це сукупність множини можливих кривих х{1), кожна з яких становить лише окремі реалізації випадкового процесу Х(і). Можливі графіки випадкових процесів зображено на рис. 7.1.

Ймовірність того, що процес відбуватиметься за якою-небудь певною заздалегідь заданою кривою, нескінченно мала. Можливий характер перебігу випадкового процесу оцінюється ймовірнісними характеристиками, подібними до характеристик безперервної випад-

свою функцію розподілу. Для випадкової величини Х(ї{) функція розподілу має вигляд

вірностей випадкового процесу Х{і). Частинна похідна від неї

а

Рис. 7.1

370

7.1.Уявлення про випадкові процеси

ми пишеться одновимірною щільністю розподілу.

Функції Рх (х, і) і и>, (х, і) є найпростішими характеристиками ви- 'м нового процесу. Більш повну характеристику випадкового проце-

і • и двовимірна функція розподілу

Р2(х{ ,Х2;Ґі9І2) = р{Х(І{) < X,; Х(Г2) < х2 },

і» і дорівнює ймовірності того, що при/! значення випадкового про-

Аналогічно можна визначити також багатовимірні функцію й ип'їьність розподілу.

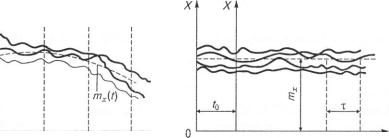
Випадкові процеси можуть бути стаціонарними або нестаціонарними. Якщо ймовірнісні характеристики випадкового процесу не заіг і .їїі, від вибору моменту часу г, тобто інваріантні відносно початку меиіку, то випадковий процес називається стаціонарним, у противному разі — нестаціонарним. Графік випадкового стаціонарного проїм -гу зображено на рис. 7.1, б.

І Імовірнісні характеристики стаціонарного процесу не зміню- інм.ея протягом часу, тобто

Р{х, і)=Г(х);

>у(х, і) = и>(х).

< іаціонарні випадкові процеси мають дуже важливу властивість, ні ,і називається ергодичною. Суть цієї властивості така: будь-яке се- !" і не за множиною з імовірністю «одиниця» (практично достовірно) іирпшіоє відповідному середньому за часом, тобто

її л., де рискою позначено усереднення за часом. Далі користувати- мешся загальним символом усереднення М{-}9 яким позначатимемо

• • редпеппя за множиною або за часом, тобто

М{х) = хсер = х; М{х2} = (х2)сер = х 2 .

371

7.2

Характеристики стаціонарних випадкових процесів

До основних характеристик стаціонарних випадкових процесів належать математичне очікування,

Якщо врахувати ергодичну властивість, то

характеризує міру розкиду значень випадкового процесу стосовно його середнього значення і дорівнює різниці середнього значення квадрата процесу і квадрата середнього значення процесу. Квадратний корінь із дисперсії визначає середньоквадратичне відхилення

372

7.2. Характеристики стаціонарних випадкових процесів

Кореляційна функція (або, що те саме, автокореляційна) характе- ри і\« ( і умінь залежності (кореляції) між значеннями процесу, відда- і ними один від одного на час т, тобто оцінює швидкість змінюванні і пипадкового процесу протягом часу. Вона становить середнє зна-

• і,і' 111 пості кореляційну функцію можна визначити як середнє за ча- I им

Кореляційна функція стаціонарного процесу має такі властивості. І Кореляційна функція є парною функцією зсуву т. Замінивши у

инр.і п (7.10) і на / - т, дістанемо

Ііппадковий процес, середнє значення якого дорівнює нулю, напій, и и,ся центрованим. Для такого процесу

Кх( 0) = вх.

* Значення кореляційної функції при т = 0 є найбільшим:

і!! онесіи цю нерівність, розглянемо очевидну нерівність

[х(ґ) - х(і + т)]2 > 0,

І м» ої

х2(1) + х2(! -ь т) > 2 х ( ї ) х(і + т).

373

Візьмемо середнє за часом від правої та лівої частин останньої нерівності. Тоді, з урахуванням виразів (7.12) і (7.10), дістанемо

М{х2( ї) + х2(ґ + т)} = 2 М{х2(і)} = 2ЛД0);

2М{х(1)х(1 + т)} = 2Кх(т),

звідки

4. При т —> оо кореляційна функція дорівнює квадрату середнього значення випадкового процесу

Для центрованого випадкового процесу Ях( оо)= 0.

5. Значення кореляційної функції звичайно зменшується при збільшенні т, оскільки зв'язок між віддаленими значеннями х, як правило, слабшає.

Для стаціонарного випадкового процесу кореляційна функція становить універсальну характеристику. Обчислити її досить просто, якщо мати експериментально зняті криві, тобто окремі реалізації випадкового процесу. Одну з таких реалізацій зображено на рис. 7.2. Для неї, згідно з виразом (7.11),

1

Т - т

Чим більше час Т і чим більше експериментально знятих кривих, тим точніше можна визначити кореляційну функцію.

За відомою кореляційною функцією можна знайти такі ймовірнісні характеристики:

• середнє значення випадкового процесу

тх = ^Кх( оо);

374

7.2.Характеристики стаціонарних

випадкових процесів

с е р е д нє з н а ч е н н я квадрата в и п а д к о в о г о процесу

М{х2(ї)}=Ях( 0);

д и с п е р с і ю

0 х = К х ( 0 ) - К х ( о о ) ;

середньоквадратичне відхилення

а , = Л / Л , ( 0 ) - / ? » .

Кореляційна ф у н к ц і я має п е в н и й сенс т а к о ж для детермінованих обмежених процесів. Я к п р и к л а д в и з н а ч и м о к о р е л я ц і й н у ф у н к ц і ю і ні постійної та гармонічної дій.

І І Приклад 7.1. Визначити кореляційну функцію постійної дії х(1) = а.

Р о з в ' я з а н н я . За формулою (7.11) дістанемо

375

обчислимо таким чином. Оскільки підінтегральний вираз є періодичним з періодом повторення 7і/ш, то інтеграл можна подати у вигляді суми інтегралів з періодами від (к - 1)я/со до /ся/со, де к = ±1; ±2; ...

При к = 1

672 С0

2тп І* соз(2со/ + сот + 2^) сії = 0.

Для будь-якого к дістанемо інтеграл косинуса за цілий період, який дорівнює нулю. Отже,

Ііт —1 І гг/9[-со$(2со/ + сох + 2ф)]г// = 0

т

і остаточно

Кореляційні функції більшості стаціонарних випадкових процесів можна подати у вигляді лінійних комбінацій кореляційних функцій трьох типів:

Графіки цих кореляційних функцій зображено на рис. 7.3.

Для оцінки статистичного зв'язку між двома випадковими про-

цесами Х(і) і ¥(1) застосовується поняття взаємної кореляційної функції

Яху(т), яка визначається за формулою

тобто взаємна кореляційна функція у разі зміни знака зсуву т змінює порядок своїх індексів.

При т = 0

Яху(0)=М{х(Г)у(Г)}у

тобто початкове значення взаємної кореляційної функції дорівнює середньому значенню добутку випадкових процесів.

376

7.3. Спектральна щільність стаціонарних випадкових процесів

Рис. 7.3

Якщо середні значення процесівтх і ту відрізняються від нуля, то

КхУ(00) = тхту

Для не зв'язаних один з одним випадкових процесів

І Іим пояснюється такий вираз: процеси корелюють або не корелю-

ють, що означає, чи є між ними статистичний (імовірнісний) зв'язок, чи немає.

7.3

Спектральна щільність стаціонарних випадкових процесів

Поняття про спектральну щільність пов'язано з розкладом кривої стаціонарного випадкового про-

іпгу на гармонічні складові.

Спектральна щільність 8А.(со) — це частотна функція, яка характе- ри і\ч спектральний (частотний) склад процесу. Вона є частотною ірактеристикою для середніх значень квадратів амплітуд гармонік,

п.і які розкладається випадковий процес.

( пектральна щільність дає можливість використовувати частотні ір.іічтеристики САК для дослідження якості процесу регулювання у

р.і я випадкових дій.

377

Замінивши в (7.21) т на -т, оо на -со і врахувавши парність кореляційної функції Ях(т), дістанемо

5Л.(со) = 5і, (-со),

тобто спектральна щільність є парною функцією частоти.

Оскільки спектральна щільність і кореляційна функція є парними дійсними функціями, формули (7.21) і (7.22) іноді можна подати

Зв'язок між5Л.(со)і /?х(т)такий, що чим ширше графік кореляційної функції ЛЛ,(т),тим вужчий графік спектральної щільності і навпаки.

Взаємна спектральна щільність двох статистично зв'язаних випадкових стаціонарних процесів визначається за формулою

Спектральні щільності випадкових процесів, кореляційні функції яких мають вигляд (7.17)—(7.19), визначаються відповідно за формулами

378

7 . 3 . Спектральна щільність стаціонарних випадкових процесів

(а + усо0 )р2 + (а - усо() )со2

мо \\2 = а 2 + сод.

Графіки спектральних щільностей 8Хі (со) і 8Хі (ш) зображено на рис. 7.4. Крива 2 на рис. 7.4, б відповідає меншим значенням (3 і більшим значенням а порівняно з кривою 1.

Випадковий процес, який має однакові значення спектральної щільності для будь-яких частот від -оо до +оо, називається білим шумом. Усі частоти для білого шуму однаково ймовірні, спектральна щільність і кореляційна функція матимуть вигляд

5х(й)) = N = соп8і,

'іо й(т) — дельта-функція. Отже, кореляційна функція білого шуму А\ (т) дорівнює нулю для всіх т Ф 0, тобто становить імпульсну функцію.

Випадковий процес зі сталою спектральною щільністю фізично ін реальний, оскільки йому відповідають нескінченно великі диспер-

379