
Komyak_A_I_Molekulyarnaya_spektroskopia
.pdfвысокой точностью в приближении покоящихся ядер. Результат такого решения в большинстве случаев хорошо удовлетворяет опыту (эксперименту). Таким образом, в адиабатическом приближении задачи о движении электронов и ядер в молекуле разделяются. Пределы применимости указанного подхода определяются соотношением энергий колебаний и разности энергий различных электронных состояний. Если энергия колебаний молекулы больше или сравнима по порядку величины с разностью энергий электронных состояний, то адиабатический подход к рассмотрению таких электронно-колебательных состояний неприменим, и необходимо привлекать более общие неадиабатические методы решения таких задач.
В адиабатическом приближении электронно-колебательная волновая функция в силу разделения электронного и колебательного движений представляется в виде произведения волновых функций, описывающих электронное (е) и колебательное ( ) движения:
e (r, R) e (r, R) (R) , |
(6.15) |
где r и R – электронные и ядерные координаты соответственно. В рамках этого приближения в силу медленности ядерных движений электронная волновая функция зависит от ядерных координат R как от параметров. Физический смысл этой зависимости заключается в том, что для каждой конфигурации ядер, совершающих медленные по сравнению с электронами движения, стационарные состояния электронов в принципе различны. Параметрическая зависимость электронной волновой функцииe r, R от ядерных координат в адиабатическом приближении
определяются оператором электронно-колебательного взаимодействия, входящим в потенциальную энергию взаимодействия электронов и ядер V(r, R). Действительно, запишем гамильтаниан молекулы в виде
|
|
|
ˆ |
ˆ |
ˆ |
ˆ ˆ |
V , |
(6.16) |
|
|
|
H |
Te T V (r, R) Te T Vee Ve |
||||
где |
ˆ |
и |
ˆ |
– |
операторы |
кинетической энергии |
электронов |
и ядер |
Te |
T |
|||||||
соответственно, а Vee ,Ve и V -потенциальные энергии взаимодействия
электронов, электронов и ядер и ядер между собой. Уравнение Шредингера запишется в виде
ˆ |
(6.17) |
H e Ee e . |
С учетом ранее приведенного вида электронно-колебательной
волновой функции (6.15) получим равенство |
|
|
ˆ |
T e V (r, R) e Ee e , |
(6.18) |
Te e |
||
|
303 |
|



Проблема учета электронно-колебательного взаимодействия в рамках адиабатического приближения при расчете колебательной структуры электронных переходов была рассмотрена в 30-х годах прошлого столетия Герцбергом и Теллером. Смысл их рассмотрения сводится к следующему.
Пусть оператор, описывающий взаимодействие электронов и ядер, равен
Ve |
Z e |
2 |
, |
(6.27) |
Zi |
|
|||
i, |
|
|
|
где суммирование ведется по всем электроном и ядрам. Представим этот оператор в виде ряда Тейлора по координатам ядер в точке равновесия конфигурации молекулы, когда R R0 :
V V (z , R |
) Ve |
(R R |
) ... |
(6.28) |
R R R 0
Внормальных координатах выражение (6.28) запишется в следующем
виде: e e 0i 0
Ve (r,Q) Ve (r,0) Ve |
|
Qk ... |
(6.29) |
||||||||
|
|
|
|
|
k |
Q |
|
|
|
||
|
|
|
|
|
k |
Qk 0 |
|
||||
|
|
|
|
|
|
|
|
|
|
||
Следует иметь в виду, что выражения (6.28) |
|
и (6.29) справедливы |
|||||||||
только тогда, когда выполняется условие |
|
|
|
|
|
|
|||||
|
ri R 0 |
|
|
|
R R 0 |
|
, |
|
(6.30) |
||
|
|
|
|
|
|||||||
т. е. амплитуды колебаний ядер много меньше расстояний от электронов до ядер. Используя выражение (6.29), получаем для электронной части адиабатического гамильтониана молекулы характерное для теории возмущений выражение
ˆ |
ˆ |
|
|
|
V , |
(6.31) |
He |
Te (ri ) Vee (ri ,rj ) Ve (ri ,0) |
|||||
где V – оператор возмущения, который имеет вид |
|
|
||||
V Ve |
|
|
Qk ... Ak Qk |
... |
(6.32) |
|
|
|
|||||
k |
Q |
|
|
k |
|
|
k |
|
Qk 0 |
|
|
||
|
|
|
|
|
|
|
Если мы рассматриваем колебательные состояния молекулы, расположенные вблизи минимума потенциальной поверхности, то в операторе возмущения (6.32) можно ограничиться первым, линейным по
306

нормальным координатам членом. В этом случае для невырожденных электронных состояний электронная составляющая электронноколебательной волновой функции с учетом членов первого порядка малости по теории возмущений равна
t (r, Q) t (r, 0) |
u |
Akt |
t |
|
Qkt |
u (r, 0). |
(6.33) |
|
|
|
|
|
|||||
E0 |
E |
0 |
||||||
u t k |
|
|
|
|||||
et |
|
|
eu |
|
|
|
||
В выражении (6.38) индекс t у оператора Akt и нормальных координат Qkt показывает, что нормальные координаты берутся в электронном
состоянии t. Таким образом, вибронные переходы, запрещенные по симметрии в кондоновском приближении, могут быть разрешены в более точном, учитывающем электронно-колебательное взаимодействие, герцберг – теллеровском приближении.
Действительно, подставив электронную волновую функцию в виде (6.33) в (6.24), получим для матричного элемента дипольного момента перехода следующее выражение:
|
|
|
|
|
|
Fstk |
|
|
|
|
|
|
|
|
Ftsk |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
t, |
pˆ |
s, t |
pˆ |
|
|
|
Qk |
|
|
|
Qk |
|
|
, (6.34) |
|||||||||||||||||||||||||
s |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
t |
Akt |
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Fstk |
|
|
|
|
|
u |
pˆ |
s |
, |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Eet0 Eeu0 |
|
|
t |
|
pˆ |
|
s |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
u t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Ftsk |
|
t |
|
|
pˆ |
|
|
u |
|
|
|
|
u |
|
Aks |
|
s |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
u s |
|
t |
pˆ |
s |
|
|
|
|
Ees0 Eeu0 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Если переход запрещен по симметрии (или вероятность его близка к нулю), т. е.  t pˆ s
t pˆ s 0, то первый член в (6.34), соответствующий
0, то первый член в (6.34), соответствующий
кондоновскому приближению, будет равен нулю (или очень мал). Однако следующие, герцберг – теллеровские члены пропорциональны
интегралам типа  u pˆ s
u pˆ s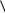 и
и  t pˆ u
t pˆ u , т. е. вероятностям переходов s u или
, т. е. вероятностям переходов s u или
u t , которые могут быть отличны от нуля, и они дадут ненулевые вклады в полную вероятность перехода. Таким образом, переход из состояния s в t происходит как бы через промежуточное виртуальное состояние u, смешанное вибронно с одним из комбинирующих состояний s или t.
307

Если рассматривается электронно-колебательный переход между электронными состояниями, одно из которых основное, скажем s, то выражение (6.34) несколько упрощается. Как правило, можно не учитывать вибронное возмущение основного электронного состояния,
например |
|
s, |
по сравнению с |
возбужденным, |
так |
как |
обычно |
||||||||||||||
E0 |
E0 |
|
E0 |
E0 . |
В |
этом |
случае |
получаем |
из |
|
(6.34), так |
||||||||||
es |
eu |
|
|
et |
eu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
как Fstk 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fstk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
t, |
pˆ |
s, |
t |
pˆ |
s |
|
|
Qk |
|
. |
(6.35) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, видим, что в герцберг-теллеровском приближении колебательная структура электронных спектров определяется не только интегралами Франка – Кондона, как в кондоновском, но еще и интегралами наложения колебательных волновых функций герцберг – теллеровского типа
|
|
|
(6.36) |
|
(Q ) f (Q) (Q )dQ , |
||
где f (Q) i (Qis ) , |
а i |
есть осцилляторная |
функция, |
i |
|
|
|
соответствующая i-м нормальной координате в s-м электронном состоянии, а также интегралами электронно-колебательного
взаимодействия типа  t Akt u
t Akt u .
.
Таким образом, учет электронно-колебательного взаимодействия уже в рамках адиабатического приближения приводит к «перемешиванию» электронных состояний, полученных в приближении Франка – Кондона. Следовательно, вибронные переходы, запрещенные по симметрии в кондоновском приближении, могут быть разрешены в более точном, учитывающем электронно-колебательные взаимодействия, герцберг – теллеровском приближении. В результате примешивания (под воздействием колебательного возмущения) состояний, моменты перехода в которые из основного велики, часть интенсивности этих переходов как бы передается вибронным переходам из основного в рассматриваемое электронное состояние (и из него в основное состояние) Механизм Гегцберга – Теллера поэтому часто называют вибронным заимствованием интенсивности.
В качестве примера рассмотрим применение формулы (6.35) для интерпретации спектра поглощения бензола в ультрафиолетовой области
(см. п. 6.6), соответствующий переходу 1A1g 1B2u . Этот переход
308
запрещен по симметрии, следовательно, первый член в формуле (6.35) равен нулю. Второй член в формуле (6.35) отличен от нуля. Теоретикогрупповой анализ показывает, что второй член отличен от нуля только в том случае, если электронное состояние t имеет симметрию E1u , а
оператор Akt симметрию e2 g (оператор имеет ту же симметрию, что и нормальное колебание Qk ). Это означает, что колебания симметрии e2 g
осуществляют смешивание состояний 1B2u с состоянием 1E1u , переход в которое из основного разрешен.
6.5. ОБЩАЯ ХАРАКТЕРИСТИКА
ЭЛЕКТРОННЫХ СПЕКТРОВ МНОГОАТОМНЫХ МОЛЕКУЛ
По виду электронные спектры можно подразделить на сплошные,
диффузные (полосатые) и дискретные. Сплошные спектры пред-
ставляют собой одну колоколообразную полосу шириной порядка нескольких тысяч см–1, лишенную каких-либо деталей колебатель-
ной структуры.
На рис.6.15,а приведены спектры поглощения (1, 2) и флуорес-
ценции (1', 2') 3,6-тетраметиламинофталимида в парах (1 и 1') и в растворе пропилового спирта (2 и 2') при комнатной температуре.
Поглощение в парах и растворах не изменяется, если судить о форме кривой, за исключением положения максимума полосы, который в растворе значительно сдвигается в красную сторону.
Диффузные спектры представляют собой одну или несколько по-
лос шириной сотни см–1, на которых заметны детали их колебатель-
ной структуры. Примерами могут служить спектры молекул в газах при комнатной температуре, жидкостях и твердых телах.
На рис. 6.15, б приведен спектр поглощения 9,10-
диаллилантрацена в глицерине при комнатной температуре. Спектр обнаруживает явно полосатую структуру с расстоянием между мак-
309
симумами полос, равном примерно 1400 см–1. Эта величина соответ-
ствует полносимметричному колебанию типа ag молекулы антраце-
на, равному 1405 см–1.
Дискретные спектры (обычно их называют квазилинейчатыми) с
шириной линий несколько см–1, наблюдаются для газовых молекул при низких давлениях или в охлажденных потоках, а также в жидко-
стях или кристаллах при низких и сверхнизких температурах. На рис. 6.15, в приведен спектр возбуждения (поглощения) молекулы
1,3-аминофталимида, охлажденной в сверхзвуковом потоке. По сво-
ей структуре этот спектр молекулы аналогичен дискретному спек-
тру атома. Квазилинии имеют ширину 2 – 3 см–1, и особенно одна из них имеет высокую интенсивность и повторяется в спектре не-
сколькими квантами в комбинации с частотой 0–0 перехода
~ |
|
1 |
). |
( 0 |
0 |
26563 см |
Рассмотрим образование сплошных полос поглощения и испуска-
ния многоатомной молекулы, анализируя рис. 6.16.
310


Eкол
E'кол
(E'кол)
0-0
Eкол
E''кол
(E''кол1) Iотн
0,5
300 |
500 |
|
Рис. 6.16. Схема образования сплошных спектров поглощения и испускания многоатомных молекул. Волновой стрелкой указана внутримолекулярная релаксация
|
|
|
и |
На нем приведены самое низшее электронное состояние Eэл |
|||
верхнее возбужденное электронное состояние |
|
со своими колеба- |
|
Eэл |
|||
тельными подуровнями энергии. Для наглядности колебательные уровни отмечены дискретными отрезками прямых линий. С учетом взаимодействия колебательные уровни могут перекрываться, обра-
зуя квазинепрерывную последовательность.
Слева приведены функции, характеризующие населенности коле-
бательных подуровней нижнего ( E ) и верхнего ( E ) электронного
эл эл
312
