Глава 6. Средние величины

Средние величины в статистике выполняют роль обобщающих показателей, характеризующих изучаемую совокупность единиц по какому-либо признаку.

При изучении вопроса о применении средних величин особое внимание следует обратить на то, что каждый их вид определяется в зависимости от конкретного экономического условия и от поставленной задачи. В противном случае средняя даст ошибочный результат и будет являться искаженной характеристикой изучаемой статистической совокупности.

Следует уяснить, что средняя рассчитывается по качественно однородной совокупности, значения которой примерно одного порядка. Это основное условие применения средней.

Средние величины в статистике являются величинами именованными и выражаются в тех же единицах, в которых выражен признак.

В статистическом анализе используют следующие виды средних величин: арифметическая простая, арифметическая взвешенная, гармоническая, геометрическая, средняя квадратическая, структурные средние медиана и мода.

Средняя арифметическая простая применяется в том случае, когда каждая единица совокупности имеет свое конкретное значение, которое встречается один или одинаковое число раз, т.е. когда средняя рассчитывается по несгруппированным единицам совокупности. Она рассчитывается по формуле:

x = ∑nxi ,

где xi – значения показателя; n – число значений.

Средняя арифметическая простая равна частному от деления суммы индивидуальных значений признака на их количество.

Пример. Рассчитаем среднюю арифметическую по следующим данным:

В данном случае применима средняя арифметическая простая:

Таким образом, средняя выработка деталей на одного рабочего составляет

1,0 тыс. шт.

Если исходная информация дана на определённую дату и интервалы между ними равны, то средняя величина определяется по формуле средней хро-

нологической:

45

Пример. Имеются данные о численности сотрудников предприятия: на

01.01.2002 – 40 чел., 01.03.2002 – 60 чел., 01.05.2002 – 80 чел. Средняя чис-

ленность сотрудников за квартал составляет:

x = (40÷2) +60+(80÷2) =60 чел. 3−1

Средняя арифметическая взвешенная применяется в том случае, когда имеется некоторая повторяемость значений единиц совокупности. Она рассчитывается по формуле:

x = ∑xi fi ,

∑ fi

где f – частота (повторяемость признака).

Средняя арифметическая взвешенная равна сумме произведений вариант (x) на их частоты или веса (f), поделенной на сумму частот.

Пример. По данным о распределении рабочих-наладчиков по стажу работы и квалификации участка одного из цехов промышленного предприятия рассчитаем среднюю арифметическую взвешенную (табл. 6.1). Определим:

1)средний разряд рабочих каждой возрастной группы;

2)средний стаж рабочих участка.

Для нахождения среднего разряда рабочих каждой группы следует применять среднюю арифметическую взвешенную: в качестве веса (f) выступает конкретный разряд рабочих. Так, для рабочих со стажем работы до 10 лет средний тарифный разряд составит:

Для рабочих со стажем работы 10-20 лет средний тарифный разряд составит:

И так далее по другим возрастным группам.

Длянахождениясреднегостажарабочихнаучасткеприменяюттужесреднюю арифметическуювзвешенную, ноужедляинтервальногорядараспределения:

46

x = ∑xi fi ,

∑ fi

Для того, чтобы вычислить среднюю арифметическую интервального ряда, надо сначала определить среднюю для каждого интервала, а затем среднюю для всего ряда.

Средняя для каждого интервала определяется как полусумма верхних и нижних границ, т.е. по средней арифметической простой. Так, для первой группы со стажем работы до 10 лет среднее значение интервала составит

(0 + 10) : 2 = 5; 10-20 лет – (10 + 20) : 2 = 15 и т.д.

x = ∑∑xi fi fi ={[(0+10):2]×9+[(10+20):2]×7+[(20+30):2]×3+[(30+40):2]×2}:(9+7+3+2)

== 295 : 21 = 14 лет.

Таким образом, средний стаж рабочих по совокупности – 14 лет. Можно также рассчитать средний стаж рабочих по соответствующим квалификационным группам. Так, для рабочих 5-го разряда средний стаж составит:

X 5 = (5 × 4 + 15 × 2 + 25 × 1) : (4 + 2 + 1) = 10,7 года.

Аналогичные расчеты можно произвести по другим квалификационным группам.

Если нижняя граница интервала отсутствует в первой группе, то середина интервала определяется вычитанием из верхней границы интервала полусуммы величины интервала последующей группы. Если отсутствует верхняя граница последней группы, то середина интервала определяется прибавлением к нижней границе интервала полусуммы интервала предыдущей группы.

Часто в практике приходится определять среднюю из относительных величин. Здесь в качестве весов выступает частота (f) или частность. При расчете средней из относительных величин вариантами (x) являются эти относительные величины, а весами (f) – соответствующее каждой относительной величине основание.

Пример. Необходимо определить средний процент работающих студентов по трем факультетам по данным табл. 6.2.

x= ∑x f = 90 1500 +80 1000 +50 500 = 80%.

∑f 3000

47

Для упрощения расчета средних величин необходимо использовать некоторые свойства средних.

Свойства средней арифметической:

1. Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин:

2.Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю, т.к. сумма отклонений в одну сторону погашается суммой отклонений в другую, т.е. средняя выступает равнодействующей:

∑(xi − x) fi = 0.

3.ЕсливсевариантыуменьшитьилиувеличитьнапостоянноечислоА, тосредняяарифметическаясоответственноуменьшитсяилиувеличитсянатужевеличину:

4. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно уменьшится или увеличится в А раз:

5. Если все веса уменьшить или увеличить в d раз, то средняя арифметическая от этого не изменится:

Перечисленные свойства средней арифметической позволяют в случае необходимости упрощать расчеты путем замены абсолютных частот относительными, уменьшать варианты на какое-либо число А, сокращать их в k раз и рассчитывать среднюю арифметическую из уменьшенных вариантов, а затем переходить к средней первоначального ряда. Такой способ называется «способом условного нуля» или условной средней или «способом моментов».

Пример. Имеются данные о дневной выработке рабочих (табл. 6.3). Необходимо определить среднюю выработку, используя свойства средних.

Таблица 6.3

48

Для определения средней выработки по уменьшенным данным (свойство 4) необходимо из x вычесть A = 40, затем уменьшить эти значения в 5 раз. Частоты уменьшим в 20 раз (свойство 5). Числа берем исходя из логики упрощения решения.

Новая средняя x будет равна сумме произведений сокращенных вариант на частоты, поделенной на сумму сокращенных частот:

Следующим шагом будет переход к первоначальному значению. Для этого полученное значение умножим на 5 (т.к. делили на 5) и прибавим 40 (т.к. вычитали 40):

x = x′ 5 + 40 = −0,08 5 + 40 = 39,6 дет.

Средняя гармоническая применяется в том случае, когда известны один из сомножителей и само произведение. Обозначим x·f через М, тогда средняя гармоническая будет определяться по формуле:

где х – известный сомножитель; М – известное произведение.

Пример. Требуется вычислить средний процент выполнения плана по выпуску продукции цехом, состоящим из четырех участков (табл. 6.4).

Применение средней арифметической простой исключается, так как процентные соотношения не подвергаются суммированию. Для решения данной задачи следует применить формулу средней гармонической. Критерием правильности применения данной формулы является то, что числитель ( ∑M )

представляет собой суммарный объем выпуска продукции участками цеха, а знаменатель ( ∑Mx ) – суммарную величину выпуска продукции по плану.

Подставляя числовые данные в формулу, получаем:

49

x = ∑∑MM =(6500+7300+6900+5300):(6500:1,013+7300:0,905+6900:1,025+5300:1,019)=

x

= (26000:26415,8) × 100% = 98,4%.

Средний процент выполнения плана по выпуску продукции цехом соста-

вил 98,4%.

В тех случаях, когда произведение x f = M одинаковое или равно единице, применяется средняя гармоническая простая, вычисляемая по формуле:

Пример. Две автомашины прошли один и тот же путь. Одна – со скоростью 60 км/час, другая – 80 км/час. Необходимо определить среднюю скорость автомашин.

В данном случае произведения одинаковые, т.к. путь один. Применяем среднюю гармоническую простую:

стой скорость равна (60 + 80) : 2 = 70 км/час, что неверно.

Средняя геометрическая используется для определения среднего темпа роста явления за рассматриваемый период динамики. Она рассчитывается двояко:

где k1, k2, …, kn – коэффициенты динамики по отношению к предыдущему периоду; n – число коэффициентов динамики; х1 и хn – соответственно первый и последний абсолютные уровни ряда динамики; (n-1) – число абсолютных уровней ряда динамики.

Пример. Требуется определить средний темп роста выпуска литья в оболочковых формах в литейном цехе завода за пятилетний период по данным табл. 6.5.

Произведем расчет:

x= 4 1,059 1,073 1,093 1,003 × 100 = 105,6% или

x= 5−1 286,6 : 230,1 × 100 = 105,6%.

Таким образом, средний темп роста выпуска литья составил 105,6%.

50

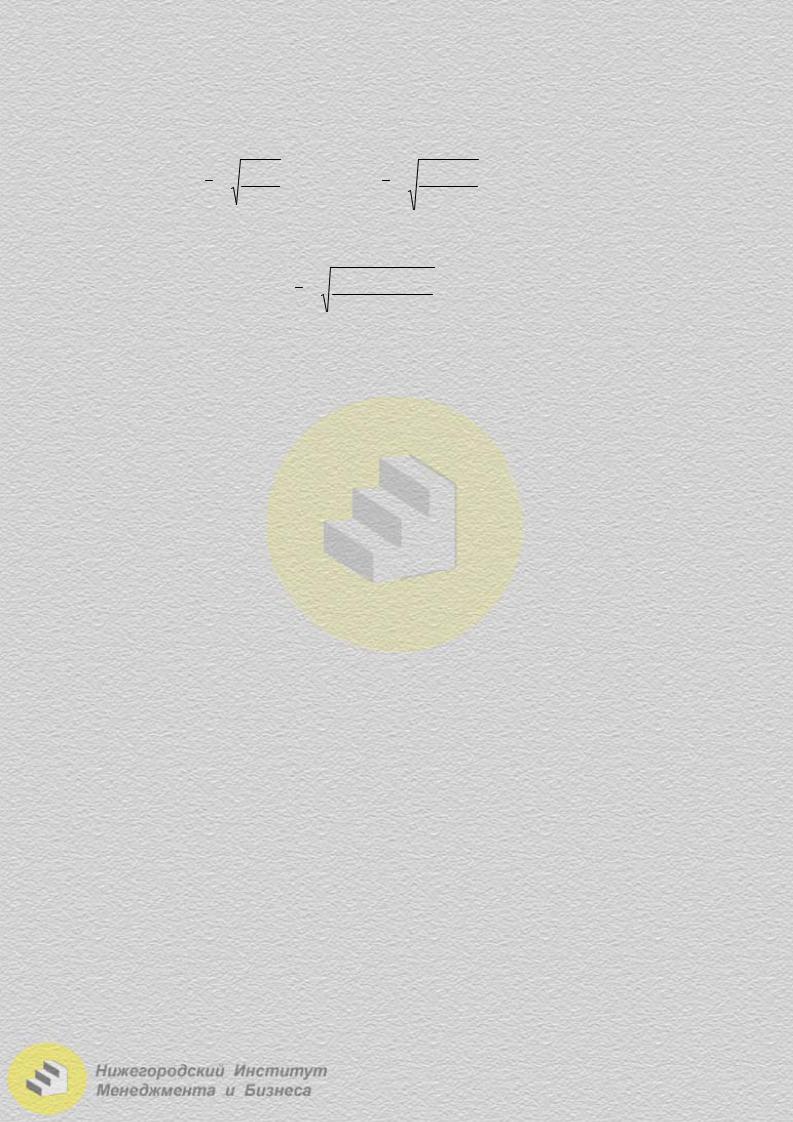
Средняя квадратическая применяется в тех случаях, когда осредняются величины, входящие в исходную информацию в виде квадратных функций. Определяется она по формулам:

Пример. Имеются следующие данные о диаметрах труб: диаметр 1-й трубы – 25 см, 2-й – 40 см, 3-й – 50 см. Средний диаметр трубы равен:

Медиана и мода

Для изучения структуры исследуемой совокупности применяют так называемые структурные средние: медиану и моду.

Медианой в статистике называют такое значение признака, которое расположено в середине упорядоченного ряда.

Медиана определяется по-разному для дискретного и интервального ва-

риационных рядов. Медиана дискретного вариационного ряда, расположенного в ранжированном порядке, имеет серединное значение. Если дискретный ряд включает четное число единиц, то медиана (Ме) определяется как средняя из двух центральных значений. Медиана в интервальном ряде определяется по формуле:

где x0 – нижняя граница медианного интервала (медианным называется пер-

вый интервал, накопленная частота которого превышает половину общей суммы частот);

i– величина медианного интервала;

∑f – сумма накопленных частот;

fm – частота медианного интервала;

Sm−1 – сумма накопленных частот предмедианного интервала.

По следующим данным дискретного ряда распределения, расположенного в ранжированном порядке (в порядке возрастания) определим медиану:

Так как медиана имеет значение признака, находящееся в середине упорядоченного ряда, то для данного ряда распределения она составит 9 лет. Это значит, что половина совокупности рабочих имеет стаж работы до 9 лет, половина – более 9 лет.

Несколько сложнее определяется медиана для интервального вариационного ряда (табл. 6.6).

Таблица 6.6

51

Прежде находится медианный интервал, на который должно приходиться 50% накопленных частот данного ряда, что по условию задачи 40 : 2 = 20. Сумма частот первых двух интервалов равна 19, что меньше 20. Следовательно, медианный интервал будет находиться не во второй группе, а в третьей, т.е. в пределах границ 105-110.

Подставим соответствующие значения в формулу:

Me =105 +5 (40 ÷2) −19 =105,6% . 8

Таким образом, 50% всех рабочих выполняют производственное задание менее чем на 105,6%, 50% – более чем на 105,6%.

Модой в статистике называют наиболее часто встречающееся в исследуемой совокупности значение признака.

В дискретном вариационном ряде моду определяют по наибольшей частоте. В интервальном вариационном ряде мода определяется по формуле:

Просматривая частоты ряда (число рабочих), видим, что наибольшая частота – 12. Она соответствует дневной выработке 20 шт. Таким образом, мода показывает, что в данной совокупности наибольшее число рабочих имеют выработку 20 шт. деталей в день.

Несколько иначе определяется мода для интервального вариационного ряда. В качестве примера воспользуемся данными табл. 6.6.

Сначала найдем модальный интервал, на который должна приходиться наибольшая частота; по условию задачи это будет интервал 100-105, так как ему соответствует наибольшая частота – 16 чел. Подставив соответствующие значения в формулу, получим:

Наибольшее число рабочих выполняют месячное задание на 103%.

52

Моду и медиану в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выберем самый высокий прямоугольник, который является модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника соединяем с левым верхним углом последующегопрямоугольника. Източкипересеченияопускаемперпендикулярнаось абсцисс. Абсциссаточкипересеченияэтихпрямыхибудетмодойраспределения.

Медиана рассчитывается на кумуляте. Для ее определения из точки на шкале накопленных частот, соответствующей 50%, проводится прямая, параллельная оси абсцисс, до пересечения с кумулятой. Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.

Аналогично с нахождением медианы в вариационных рядах распределения можно найти значение признака у любой по порядку единицы ранжированного ряда. Можно найти значение признака у единиц, делящих ряд на четыре равные части, на десять, сто частей. Эти величины называются квартили, децили и перцентили.

Квартили представляют собой значения признака, делящие ранжированную совокупность на четыре равные части. Различают квартиль нижний (Q1), отделяющий ¼ часть совокупности с наименьшими значениями признака, и квартиль верхний (Q3), отделяющий ¼ с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут по величине меньше Q1; 25% будут заключены между Q1 и Q2, 25% – между Q2 и Q3, а остальные 25% превосходят Q3. Средним квартилем Q2 является медиана.

Для расчета квартилей по интервальному вариационному ряду используются формулы:

xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал

определяется по накопленной частоте, первой превышающей 25%);

xQ3 – нижняя граница интервала, содержащего верхний квартиль (интер-

вал определяется по накопленной частоте, первой превышающей 75%); i – величина интервала;

– накопленная частота интервала, предшествующего интервалу,

содержащему нижний квартиль;

SQ3−1 – то же для верхнего квартиля;

fQ1 – частота интервала, содержащего нижний квартиль; fQ3 – то же для верхнего квартиля.

Пример.

Таблица 6.7

Распределение семей города по размеру среднедушевого дохода в январе 2000 г.

53

Нижний квартиль находится в интервале 600-700, накопленная частота которого равна 30%. Верхний квартиль лежит в интервале 800-900 с накопленной частотой 77%. Поэтому получаем:

Итак, 25% семей имеют среднедушевой доход менее 671 руб., 25% семей – свыше 891 руб., а остальные имеют доход в пределах 671-891 руб.

Контрольные вопросы

1.Какова экономическая сущность средней?

2.Какие формы средней рассчитываются в экономических исследованиях?

3.Какова методология расчета средней по данным интервального вариационного ряда?

4.Каковы экономический смысл и методология расчета структурных средних?

5.Какой интервал в интервальном вариационном ряде называется модальным, какой медианным?

54