геодезия конспект лекций

Вообще говоря подземная система координат может быть принята произвольно. Расстояние LП и LШ должны быть равны между собой, а

разность дирекционных углов равна повороту осей координат подземной системы координат.

Угол θ = αШ−αП используется для уточнения дирекционных углов сторон подземного полигонометрического хода.

Необходимо отметить, что ошибки измерения углов и линий в подземной полигонометрии, действующие в направлении перпендикулярно линии О1 О2 целиком входят в определение угла θ.

Данный способ ориентирования выгодно отличается от остальных. Он

позволяет получить дирекционный угол линии подземной полигонометрии непосредственно у забоя с ошибкой порядка 8". Все остальные способы, кроме гироскопического, ориентируют только первую линию хода.

3.9.1.10.Ориентирование способом соединительного треугольника

3.9.1.10.1. Геометрическая схема ориентирования

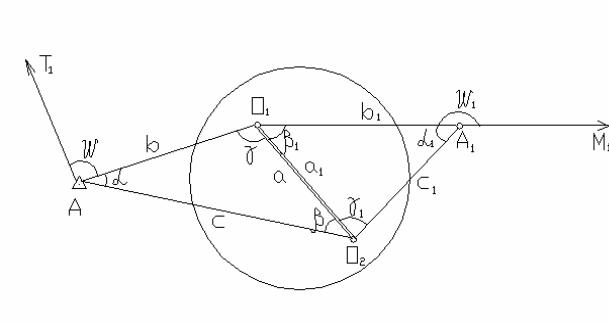
Рисунок 1 В ствол опускают два отвеса О1 и О2. В точке А с известными

координатами, расположенной около ствола, измеряют:

-угол α между направлениями на отвесы;

-примычный угол ω.

Кроме того рулеткой измеряют расстояния :

-от теодолита до отвеса в и с;

-расстояние между отвесами а.

Таким образом на поверхности получают треугольник АО1О2, в котором измерены три стороны и один угол.

Этот горизонтальный треугольник называют соединительным треугольником.

По результатам измерений могут быть вычислены значения двух остальных углов β и γ. Зная дирекционный угол направления АТ, значение примычного угла ω и углы соединительного треугольника, можно получить дирекционный угол створа отвесов О1О2:

α01-02 = αАТ1 + ω + α + β ± 180° (1)

Пользуясь элементами соединительного треугольника и координатами точки А, находят координаты отвесов X01,Y01;X02,Y02.

В подземных выработках на ориентируемом горизонте около ствола закрепляют точку А1. В этой точке измеряют углы α1 и ω1, а также стороны а1, в1, с1 подземного соединительного треугольника.

Считаем, что дирекционный угол створа отвесов под землей равен дирекционному углу на поверхности . При помощи углов подземного

соединительного треугольника и примычного угла вычисляют дирекционный угол приствольной линии А1М1 подземной полигонометрии.

Координаты точки А1 определяют по элементам подземного соединительного треугольника, принимая в качестве исходных координаты отвесов, полученные на поверхности.

3.9.1.10.2.Оптимальная форма соединительного треугольника

Форма соединительного треугольника оказывает влияние на точность вычисления углов β и γ, а следовательно на точность вычисления дирекционного угла створа отвесов (формула 1).

Угол вычисляется по формуле

Т.к. длины сторон треугольника лежат в пределах одной рулетки, то

можно принять

mв = ma = mc = ml

Тогда

Исходя из формулы (2),

sinα = a *sin β (4) b

Подставим выражение (4) в формулу (3): m

Приведем подобные члены и выполним преобразования:

Первый член правой части формулы (5) выражает влияние на точность определения угла β ошибок линейных измерений, а второй - влияние ошибки измерения угла α. Рассмотрим эти влияния отдельно.

Из формулы (6) следует, что чем меньше угол β , тем меньше будет ошибка его определения.

Путем соответствующего выбора точек прикрепления отвесов можно добиться такой формы соединительного треугольника, при которой углы α и β будут достаточно малыми.

Для малых углов отношения синусов (формула 2) можно заменить отношение тангенсов, то есть:

Формула (8) показывает, что чем больше сторона а ( расстояние между отвесами) , тем ошибки линейных измерений ml оказывают меньшее влияние.

Влияние ошибки измерение угла a на точность угла b определяется вторым членом правой части формулы (5 )

Если принять mα=4²,то

mβα=4² при b/a=1

mβα=6² при b/a=1.5 mβα=8² при b/a=2

Из вышеизложенного можно сделать следующие выводы о наивыгоднейшей форме соединительного треугольника :

1)треугольник должен быть вытянутым, угол a должен быть близок к нулю не более 3°

2)величина в/а должна быть по возможности меньше.

Но следует иметь в виду ,что приближение инструмента к отвесу у вызывает необходимость в резком изменении фокусировки трубы, что снижает точность измерения угла a. Поэтому наиболее благоприятным значением величины в/а следует считать 1,5

3) расстояние между отвесами должно быть по возможности больше . Это расстояние зависит от габарита ствола и при диаметре круглых стволов 6 м держится в пределах 4 - 5.5 м.

Это требование вытекает не только из соображений по форме треугольника, но из условий уменьшения влияния ошибки проектирования.

3.9.1.10.3.Точность ориентирования способом соединительного

треугольника

Дирекционный угол подземной ориентируемой стороны вычисляется по формуле:

αА1М = αТА + ω + α + β − β1 + ω1 − 4*180°

Запишем формулу для вычисления ошибки:

m2A1M = m2αΤΑ + m2ω + m2α + m2βξ + m2β1 + m2ω1

Углы α,ω,ω1 измеряются непосредственно теодолитом, поэтому можем записать:

mα = mω = mω1 = m

При сравнительно одинаковых формах треугольников можно принять

mβ = mβ1.

С учетом принятых обозначений, а также ошибки проектирования mпр, получим следующую формулу:

m2А1М = m2αΤΑ = 3m2 = 2m2β = m2ПР (9)

Ошибка mαΤΑ определяется из оценки туннельной триангуляции для стороны, от которой передается в подземные выработки. Эта ошибка обычно не превышает 3".

Ошибка mβ определяется по формуле (5); ml в этой формуле = 0.8мм (на основании опытных данных).

Ошибка проектирования при расстояниях между отвесами 4 - 5 м и глубине ствола около 80 м составляет 8", причем систематическая часть в пределах 6", а случайная - в пределах 5".

При m = 4-5", а = 4.5; в/а = 1.5 величина mА1М находится в пределах 8" при выполнении ориентирования при 3-х положениях отвесов.

3.9.1.10.4. Процесс ориентирования

На период выполнения ориентирования все горно-строительные работы в стволе и в выработках прекращаются. Поэтому все измерения должны быть выполняться быстро, с надежным контролем.

Работы выполняют в следующей последовательности:

1.На поверхности над стволом сооружают помост, на котором надежно закрепляют 2 лебедки с шахтными отвесами. Точки подвеса отвесов

располагают с учетом найвыгоднейшей формы соединительного треугольника.

2.К концу отвесов прикрепляют небольшой груз и производят медленный спуск отвесов. После опускания отвесы нагружают грузом от 15 до 25 кг, которые опускают в сосуды с успокоителями (вода, масло).

3.Убеждаются, что отвесы висят свободно, т.е. не касаются армировки ствола или предметов оборудования. Это проверяется посылкой "почты".

4.Производят измерения расстояний между отвесами, для чего предварительно на каждом отвесе отмечают высоту теодолита.

Измерения как наверху, так и внизу выполняют стальными рулетками при натяжении 10 кг. Натяжение осуществляется при помощи блочных штативов гирями или динамометром. Измерения расстояния производят при 3-х положениях рулетки. Расхождения не должны превышать 2 мм.

Разность расстояний между отвесами на поверхности и в шахте, с учетом поправок за температуру не должна превышать также 2 мм.

5. Измеряют расстояния от теодолита до отвесов - в и с.

Измерение линий производят от центрировочного штифта зрительной трубы.

Рисунок 2

Для контроля линейных измерений может быть измерена линейкой высота треугольника h (одновременно с измерением стороны с).

Тогда, контроль осуществляют по формуле:

Если величина h не измерялась, то применяют формулу М.С. Чремисина:

CВЫЧ = a + b - b(b + a) *α ''2

2 *a *ρ''

Расхождение вычисленной и измеренной длины не должно быть больше ±2 мм для треугольников на поверхности и ±3 мм для подземных треугольников.

6. Производят угловые измерения теодолитами типа Т2 четырьмя приемами. За начальное направление на поверхности принимают направление на пункт триангуляции, а в подземных выработках - хорошо видимый пункт подземной полигонометрии.

Указанные действия составляют один прием. Для увеличения точности и надежности, ориентирование выполняют при трех положениях отвесов.

После каждого приема перемещают с помощью специального устройства

точки подвеса отвесов точно на15мм. Причем перемещения осуществляют по перпендикуляру к визирному лучу из точек А и А1 на отвесы.

Рисунок 3

Если точно известно перемещение l, то можно вычислить теоретическое значение Δω , на которое должен измениться примычный угол ω:

Dw= l *bρ

Сходимость разности измеренных углов в подземных выработках в допустимых пределах является контролем не только правильности измерения углов, но и правильности проектирования отвесов.

Помимо контроля можно осуществить контроль и углов α, α1:

Da²= cl * r"− bl r"

Вычисленные значения Δα и Δα1 сравнивают с фактическими при измерениях. Расхождения не должны превышать:

-поверхность 12" ( в, с ~ 4 - 6 м) 8" ( в, с > 6 м )

-шахта 15" -" - 10" -"--