геодезия конспект лекций

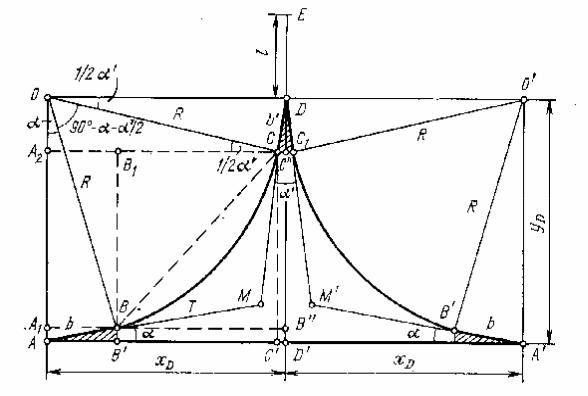
Рисунок 218 - Разбивка поворотного треугольника

Точные координаты точки D определяются как проекция ломаной АBCD соответственно на ось абсцисс и ось ординат:

xD = b ×cosα + R ×(cosα ' /2- sinα ) + b'×sinα ' /2,

yD = b ×sinα + R ×(cosα - sinα ' /2) + b'×cosα ' /2.

При разбивке поворотного треугольника на местности по пикетажу основного пути находят точку А - центр начального стрелочного перевода. Отложив от этой точки по оси пути абсциссу xD и под прямым углом ординату yD , находят положение центра стрелочного перевода тупика D. Затем отмеряя по оси основного пути от точки D’ абсциссу xD, получают точку А’- центр второго стрелочного перевода.

Если в точках А и А’ построить угол крестовины α и отложить величины b и

T = R × tg 90 - α2- α' /2, то определится положение вершин углов поворота М и

М’, т.е. будут найдены все главные точки, необходимые для разбивки поворотного треугольника.

Для контроля в точке D следует измерить углы MDD’ и M’DD’ и отрезки DM и

DM’. В пределах точности измерений эти углы должны быть равны α ’/2 , а отрезки - величине b+T . Точки M, M’ и D могут быть несколько смещены, чтобы указанные равенства были соблюдены.

Детальная разбивка криволинейных участков производится от точек BB’ и C, С’, являющихся началом и концом кривых. Ось DE тупика разбивается как продолжение

направления DD’ (по биссектрисе угла α ’).

Поворот на 180° с помощью петли. Правоповоротная петля состоит из прямого участка AG = x, основной кривой DEFG, прямой вставки DC, обратной соединяющей кривой CB, которая соединяет стрелочный перевод с прямым участком (рис. 219).

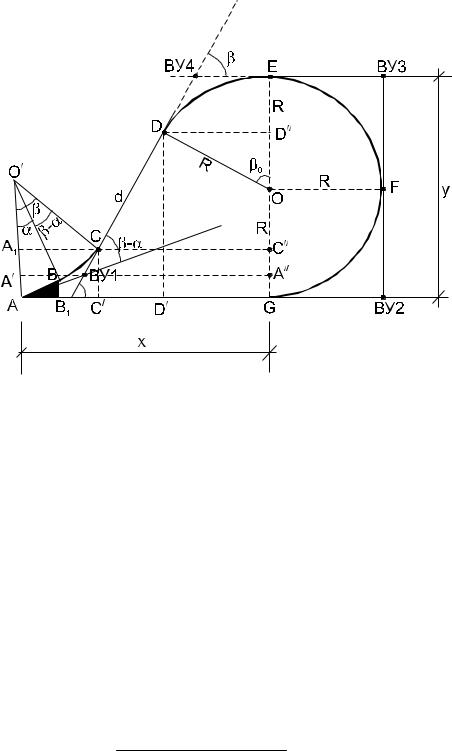
Рисунок 219 – Поворот с помощью петли

Выполним необходимые расчеты:

x = AB1 + B1C'+C' D'+D' G AB1 = b × cosa

B1C' = A1C - A1 B1 ( A' B ) = R × sinb - R × cosa C' D' = d × cosb

D' G = DD'' = R × sinb

x= b × cosa + R ×(sinb - cosa ) + d × cosb + R × sinb

y= GA''+ A'' C''+C'' D''+D'' E = 2R

y = b × sina + R × cosa - R × cosb + d × sinb + R - R × sinb

A'' C'' = O' A'-O' A1 = R × cosa - R × cosb

Угол β определяется из проекции характерных точек поворотной петли на ось y. d × sinb - 2R × cosb = R - b × sina - R × cosa

cosb = b × sina - R(1 - cosa ) 2R

Разбивку поворотной петли начинают с определения положения стрелочного перевода А. Затем на местности разбивают вершины углов поворота ВУ1, ВУ2, ВУ3, ВУ4 и конечные точки кривых B, C, D, F, E, G. От них производят детальную разбивку петли.

2.1.7. Съемка железнодорожных путей

2.1.7.1. Основные формулы

Для нормальной эксплуатации железнодорожного пути периодически производят его съемку, по результатам которой подбирают параметры кривых, наиболее близко подходящие к существующим, и определяют величины правки, или рихтовки, пути, чтобы придать ему расчетную форму.

При рихтовке пути точки кривой M, N (рис. 220.) описывают некоторые линии M’M, N’N , которые близки к нормали кривой.

Рисунок 220 - Расчет величин рихтовки пути на кривой

Так как величина сдвижки пути небольшая, то она рассчитывается по разности эвольвент кривой: проектной Эп и снятой в натуре Эс, т.е.

lM = ЭПМ - ЭСМ ; lN = ЭПN - ЭСN .

В общем виде для точки i

li = ЭПi - ЭСi .

Как известно, эвольвентой называют траекторию, которую описывает конец гибкой и

нерастяжимой нити, сматываемой с некоторой кривой. Эта кривая является

геометрическим местом центров кривизны эвольвенты, т.е. ее эволютой. Поэтому нормаль

к эвольвенте в некоторой точке М одновременно будет касательной к кривой (эволюте) в

точке В (рис. 221).

Длина эвольвенты Э от начальной точки кривой А до текущей точки В

Э = òϕdx

0

где s - длина кривой АВ, ϕ - угол между начальной касательной (линией

тангенса) в точке А и текущей в точке В.

Так как

ddsϕ = ρ1 ,

где ρ - радиус кривизны, то

эвольвенты, получаем формулу для вычисления эвольвенты круговой кривой

s

Э = 1 / Rò sds = s2 / 2R.

0

Для переходной кривой типа радиальной спирали 1/ ρ = s/ C . Тогда

s

ϕ =1/ Còsds = s 2 / 2C;

0

Э =1/ 2Còs s2 ds =s3 / 6C,

0

где С- параметр переходной кривой.

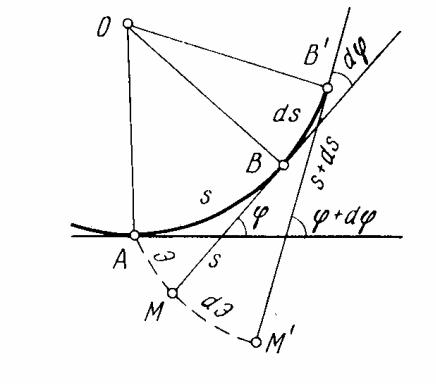
Рисунок 221 - Эвольвента

На основании вышесказанного величина снятой в натуре эвольвенты подсчитывается по приближенной формуле

i

åЭCi =åϕi di ,

1

где di -отрезки (хорды), на которые при съемке делится кривая; ϕ i - угол поворота хорд d относительно начальной линии тангенса (“азимут хорд”).

2.1.7.2. Способы съемки кривых

В зависимости от метода определения азимутов ϕ i различают несколько способов съемки кривых:

♦способ эвольвентных разностей: углы ϕ i определяют по измеренным в натуре теодолитом углам поворота хорд;

♦способ стрел изгиба: углы ϕ i рассчитывают по измеренным в натуре стрелам изгиба кривой в середине хорды d;

-фотограмметрический способ: углы ϕ i измеряют на специальном фотограмметрическом приборе по крупномасштабным аэрофотоснимкам кривой.

А) Способ эвольвентных разностей

(разработан И.В. Гоникбергом).

Рисунок 222 - Схема съемки железнодорожной кривой по способу эвольвентных

разностей На снимаемом участке пути лентой или рулеткой отмечают на внешней нитке пути

20-метровые отрезки (“элементарные хорды “) и разбивают 100-метровые пикеты, при этом конечные точки А и Е (рис. 222) выбирают на прямых участках на расстоянии 40-60 м от видимого начала и конца кривой.

На пикетах теодолитом измеряют углы поворота хорд β1,β2 ,β3... и при

возможности примычные углы γ 1,γ 2 . Одновременно на плюсовых точках +20,

+40,+60,+80 (рис. 4) способом бокового нивелирования при помощи теодолита и

горизонтально установленной рейки измеряют стрелы изгиба кривой от хорды между пикетами. Рейка закрепляется особым башмаком на гранях головки рельса, ее нулевой отсчет (“пятка”) совпадает с продольной осью рельса.

На пикетах А, В, С, D теодолит и визирные марки также центрируются над осью рельса. Стрелы изгиба измеряют дважды: в прямом (А-АВ) и обратном (В-ВА). Из двух значений стрел берут среднее, разность между ними не должна превышать 5 мм.

В пикетных точках А, В, С... по измеренным углам βi вычисляют углы поворота хорд ψ i = 180 - βi и азимуты хорд относительно линии тангенса (рис. 222):

Так как отрезки d = 20n , где n -число 20-ти метровых хорд между соседними пикетами (обычно n =5, в конечных хордах n может быть равно 3 или 4), то получим (углы

ϕ взяты в радианах)

Для вычисления эвольвент плюсовых точек используют измеренные стрелы изгиба кривой. Приращение эвольвенты на 20-ти метровый отрезок составляет

Э = dϕ - f = 20ϕ - f ,

Последовательно суммируя величины приращений находят длины эвольвент для точек

+20, +40,+60,+80.

Так как в пределах каждого пикета åDf = 0 и , следовательно,

n

å(20ϕ -Df ) = 20ϕ,

1

то для пикетажных точек должно соблюдаться равенство

б) в пределах второй половины переходной кривой от s=l/2 до примыкания к круговой кривой (s=l) :

Dl0 = Dl + ( p - (l - s )3 / 6 Rl );

в) в пределах первой половины переходной кривой от ее соединения с прямой (s=0)

до s=l/2 :

Dl0 = Dl + s3 / 6 Rl,

где s - длина переходной кривой от ее начала до текущей точки; l - общая длина переходной кривой.

li = ЭПi − ЭCi зависит, главным образом, от точности подсчета длины эвольвент

существующего пути, так как длины проектных эвольвент могут быть вычислены с достаточной точностью, т. е.:

m l = mЭС .

Определим ошибки подсчета эвольвент для пикетных точек. В формуле

примем, что величины пикетов d1 = d2 =...= di = d. Тогда:

ЭCi = d[y1 + ( y1 + y2 )+...+( yш + y2 + y3 +...+yi )] или ЭCi = d[y1 ×i + y2 (i - 1) + y3 (i - 2 )+...+yi ].

Средняя квадратическая ошибка полученной функции равна:

Если принять R=1000м, K=400 м, n=4, md/d=1/3000, mb=0.5’, то получим по формуле I mЭк=8.3 см, а по формуле II - mЭк =5.2 см, т.е. в уравненном ходе ошибка уменьшается более чем в 1.5 раза.

Для эвольвент плюсовых точек и найденной величине ошибки прибавится еще ошибка определения разности стрел изгиба, которая в среднем не превышает 5 мм.

Для рихтовки пути по плавной кривой большое значение имеет ошибка взаимного смещения соседних плюсовых точек , т.е. ошибка в подсчете приращения эвольвенты на 20-ти метровом отрезке кривой.

Б) Способ стрел изгиба.

В этом способе измеряют стрелы изгиба рельсов в середине каждой 20-ти метровой хорды с перекрытием через 10м (рис. 224). До начала измерений кривую или примыкающие к ней 40-60 метровые прямые участки разбивают на 10-ти метровые отрезки и отмечают их на рабочей грани наружного рельса. При измерениях используют два шаблона для натяжения 20-ти метровой нити и третий для измерения в средней точке нити стрелы изгиба рельса. На прямых участках стрела изгиба будет близкой к нулю.

По измеренным величинам стрел изгиба могут быть вычислены углы поворота хорд и углы поворота относительно тангенса кривой:

где k=d/2=10,00 м.