геодезия конспект лекций
.pdf
∙величину углов между красными линиями ;
∙радиусы закруглений и элементы кривых по красным линиям.
A |
l |
|
L |
l |
B |
|
|
||||
|
1 |
2 |
a |
3 |
|
|
кв.1 |
|
|
кв.2 |
|
|
11 |
12 |
|
5 |
|
|
|
13 |
10 |
|
15 |
14 |
6 |
9 |
кв.3 |
8 |
7 |
кв.4 |
|
R |
|||
|
|
Рисунок 56 – Схема проекта красных линий |
||
Геодезическая подготовка проекта заключается в определении координат углов красных линий микрорайона и кварталов и вычислении разбивочных элементов для выноса углов красных линий в натуру.
1-ый этап (подготовка) выполняется в следующей последовательности:
1.Координаты углов красных линий микрорайона определяют графически с плана. Если несколько кварталов примыкают к прямой магистрали или улице, то графически измеряют только координаты в начале и конце группы кварталов.
2.По координатам вычисляют длины красных линий L микрорайона и дирекционные углы их направлений (например, L1-4):
L1-4= 
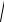 (Y4 − Y1 )2 + (X 4 − X1 )2 ;
(Y4 − Y1 )2 + (X 4 − X1 )2 ;
a1-4=arctg Y4 − Y1 .
X 4 − X 1
3. Аналитическим путем определяют координаты углов кварталов, как створных точек, расположенных на красных линиях микрорайона.
3.1. Измеряют на плане длины кварталов l (l1-2,l3-4);
3.2.Уравнивают графические размеры кварталов так, чтобы их суммарная длина с номинальной
шириной проездов была равна общей длине красной линии на участке между углами поворота ,полученной аналитическим путем.
3.3. Оставляя постоянной ширину проездов и зная суммарную длину участка, вычисляют невязку и распределяют ее на все длины кварталов:
fS = L - (m*a+n*l); fS<=0.8*M*n,
m - количество проездов; a - ширина проездов;
l - длина красной линии квартала;
L - длина красной линии микрорайона; n - число линий в створе;
M - знаменатель масштаба.
4. По уравненным длинам красных линий кварталов и дирекционным углам красных линий микрорайона находят координаты углов кварталов по внешнему контуру (т 2, 3 и.д.)
5. Координаты внутренних углов кварталов определяют, как координаты точек пересечения |
||||||||
двух прямых, заданных координатами. |
|
|
|
|
|
|
|
|
Вычисление координат выполняется с точностью до 1м. |
|
|
||||||
II -ой этап: вычисление разбивочных элементов для выноса красных линий в натуру. |
||||||||
Исходными данными для расчетов являются: |
|
|
|
|
|
|||
1. вычисленные координаты углов кварталов. |
|
|
|
|
|
|||
2. координаты точек геодезической основы в районе строительства. |
||||||||
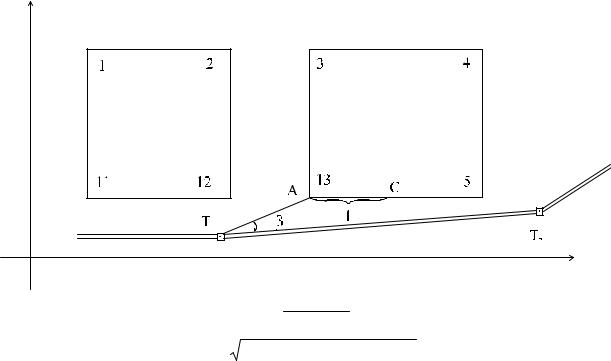
Геодезическая подготовка заключается в вычислении разбивочного угла β от стороны |
||||||||
съемочного обоснования Т1 -Т2 и разбивочной длины от точки |
||||||||
съемочного обоснования Т1 до выносимого в натуру угла квартала А (рис. 57). |
||||||||
Рисунок 57 – Проект выноса красных линий в натуру |
||||||||
β = arctg |
YA − YT1 |
− αT1−T 2 , |
||||||
|
|
|
X A − X T1 |
|
|
|
|
|
L= (Y |
A |
− Y |
)2 + ( X |
A |
− X |
T1 |
)2 |
|
|
|
T1 |
|
|
|
|||
Контроль выноса в натуру концов красных линий: на красной линии выбирают точку, |
||||||||
координаты которой не снимают с плана, а вычисляют. Для этого удаление выбранной точки (С) |
||||||||
от конца красной линии задается целым числом метров. По заданной величине удаления и |
||||||||
дирекционному углу вычисляют координаты Х и Y. Вычисляют разбивочные элементы для |
||||||||
выноса этой точки в натуру. Если после выноса в натуру точки С она оказалась в створе, то |
||||||||
конечные точки вынесены верно. |
|
|
|
|
|
|
|
|
1.2.1.3. Геодезическая подготовка проекта для выноса зданий от красных линий
Для выноса зданий от красных линий необходимо сделать ряд геодезических вычислений. Для этого необходимы следующие исходные данные:
1.Генплан с проектируемыми зданиями;
2.Характеристика зданий;
3.Координаты концов красных линий, дирекционные углы и длины;
4.Угол разворота зданий относительно красных линий;
5.Норма санитарного разрыва между зданиями.
Порядок вычислений:

1.Вычисляют координаты углов зданий, расположенных в створе красных линий:
1.1.Измеряют на плане расстояния между углами зданий и концами красной линии (l1, l2);
1.2.длину между углами зданий вдоль красной линии вычисляют по формуле :
|
|
|
l=( b1+bc.p.)/sinϕ |
|
|
|
|
||||
где |
b1 - ширина здания ; |
|
|
|
|
|
|
|
|
|
|
bc.p - норма санитарного разрыва между зданиями ; |
|
|
|
|
|
||||||
ϕ - угол разворота зданий относительно красной линий. |
|
|
|
|
|||||||
Рисунок 58 – Разбивочный чертеж для выноса проекта зданий от красных |
|
|
|||||||||
|
1.3. Уравнивают измеренные на плане длины таким образом, чтобы выполнялось |
||||||||||
|
условие: |
|
|
|
|
|
|
|
|
|
|
|
(l + l + l) − ( X |
T 2 |
− X |
T1 |
)2 |
+ (Y |
− Y |
)2 ≤ f |
доп |
; |
|
|
1 |
2 |
|
|
T 2 |
T1 |
|
|
|||
невязку распределяют в измеренные на плане длины в виде поправок с обратным знаком |
|||||||||||
пропорционально длинам. |
|
|
|
|
|
|
|
|
|
||
|
1.4. По уравненным длинам и дирекционному углу красной линии вычисляют |
||||||||||
|
приращения, а затем и координаты углов зданий. |
|
|
|
|
||||||
2. Вычисляют координаты остальных углов зданий, используя вычисленные координаты углов, |
|||||||||||
длину, ширину зданий и углы между сторонами зданий, равные 90° . |
|
|
|||||||||
На разбивочном чертеже указывают (рис. 58): |
|
|
|
|
|
|
|
||||
-положение и координаты концов красной линии;
-разбивочные элементы для выноса зданий в натуру (размеры зданий, угол разворота относительно красных линий);
-величину санитарного разрыва, координаты углов зданий.
1.2.1.4.Основные математические зависимости, используемые при расчете
геодезических элементов проекта
При геодезической подготовке проектов вычисляют координаты важнейших точек сооружений и их привязки к пунктам геодезической основы или главным осям сооружений.
Основными задачами подготовки являются:
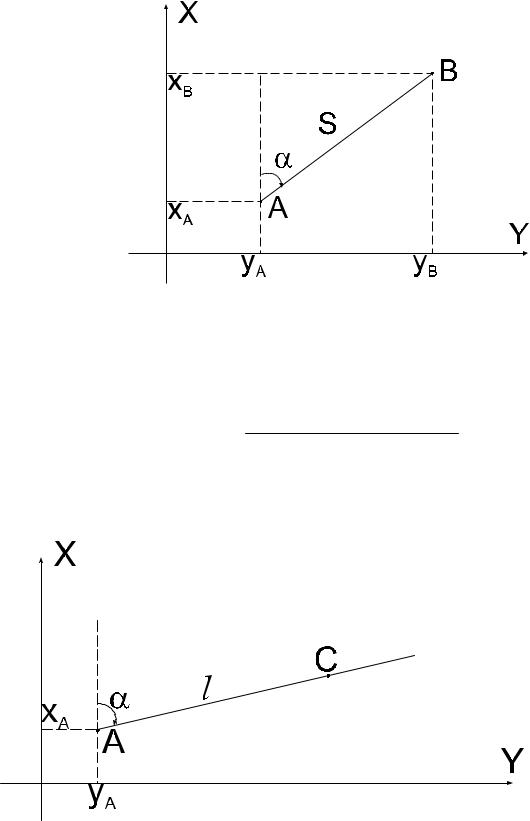
1) Определение дирекционного угла и длины линии, заданной координатами
|
Рисунок 59. |
− YA |
|
||
α A−B |
= arctg |
YB |
; |
||
X B |
− X A |
||||
|
|
||||
S = ( XB − X A ) / cosαB− A; S = (YB − YA ) / sin αB− A;
S = 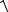
 (YB − YA )2 + ( XB − XA )2
(YB − YA )2 + ( XB − XA )2
XA, YA, XB, YB - координаты начального и конечного пунктов линии. 2) Определение координат промежуточных пунктов створа
Рисунок 60. XC=XA+l*cosα YC=YA+l*sinα
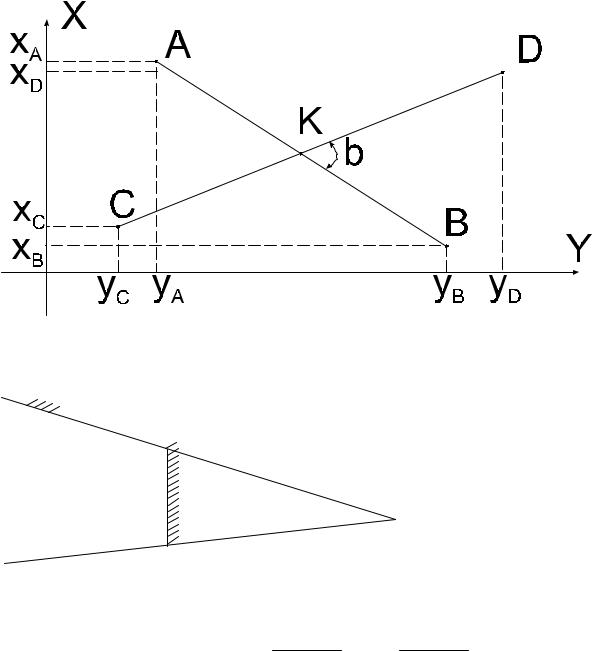
l - расстояние до промежуточной точки от начала створа (т. А)
α- дирекционный угол створа, определяемый по формуле приведенной ниже.
3) Определение координат точки пересечения двух прямых, заданных координатами
XK=XC - R(XD-XC);
YK=YC - R(YD-YC);
(XB − XA )(YC −YA ) − (YB −YA )(XC − XA )
R= |
(X |
B |
− X |
A |
)(Y −Y ) − (Y −Y )(X |
D |
− X |
C |
) |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D C |
|
|
|
|
|
B A |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 61.
4) Определение угла β , составленного двумя заданными прямыми
A
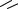



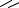
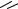
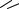
 B
B
β K
K
C









 D
D
Рисунок 62.
β=arctg YB −YA −arctg YD−YC XB −XA XD−XC
1.2.2. Геодезическая подготовка для разбивки зданий способом перпендикуляров
При отсутствии в натуре зданий между сторонами теодолитного хода и красной линией застройки, для разбивки может быть применен способ перпендикуляров.
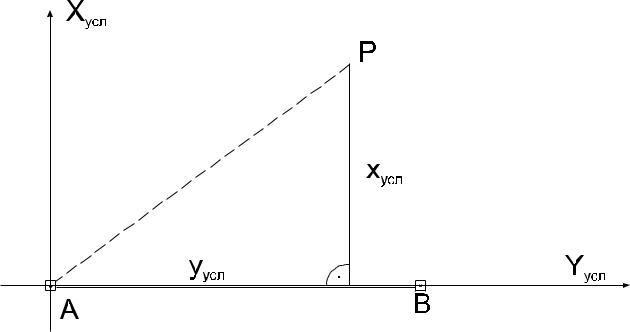
В основу способа положена разбивка проектной точки Р от линии геодезической основы АВ, чаще - от линии строительной сетки, полигонометрии, теодолитного хода, красной линии (рис. 63), взятой за начало частной системы координат, и линии АВ - в частной системы координат, и линии АВ - в качестве частной оси абсцисс.
Рисунок 63 – Схема разбивки точки способом перпендикуляров Прямоугольные координаты определяют по формулам:
Xусл = (Xр - Xа )•cosα0 + (Yр - Yа )•sinα0;
Yусл = (Yр - Yа )•cosα0 + (Xр - Xа )•sinα0,
где Xа ,Xр ,Yа ,Yр - абсолютные координаты исходной и проектной точек, α0 - дирекционный угол опорной линии АВ.
Знаки ординат указывают направление откладывания их от створных точек линии АВ: при положительной - вправо, при отрицательной - влево. Если абсцисса Х отрицательная, то ее откладывают от точки А в противоположном направлении линии АВ.
Для вынесения проекта планировки в натуру составляют разбивочный чертеж, на котором изображают схему разбивки и подписывают все разбивочные элементы и элементы для контроля:
-длины линий и их дирекционные углы;
-разбивочные углы на опорных пунктах;
-контрольные углы на определяемых пунктах;
-линейные размеры зданий;
-расстояния между сооружениями;
-координаты углов зданий.
1.2.3. Вынос на местность красных линий по заданным промерам от осей проезда
Вынос в натуру красных линий осложняется, если пользоваться только имеющимися пунктами геодезической сети. Для упрощения работ по выносу обычно закрепляют оси проезда (или для сохранения пунктов - смещенную ось) и выносят относительно оси проезда красную линию
(рис. 64 ).


tgα = |
a × sinγ |
|
; |
||||
|
|
b + a × cosγ |
|
||||
tgβ = |
b × sinγ |
|
; |
||||
|
|
a + b × cosγ |
|
|
|||
S = |
|
a |
= |
|
b |
|
|
|
sinα |
|
sinβ; |
|
|||
прямоугольные координаты: |
|
|
|
|
|
|
|
m = b + a × cosγ |
; |
|
|||||
|
|
|
sinγ |
|
|
|
|
n = a + b × cosγ . |
|
||||||
|
|
sinγ |
|
|
|
||
1.2.4. Вертикальная планировка площадки строительства методом проектных |
|||||||
горизонталей |
|
|
|
|
|
|
|
1.2.4.1.Основные математические зависимости при расчете геодезических элементов |
|||||||
вертикальной планировки |
|
|
|
|
|
|
|
1) Нахождение проектных отметок точек на наклонной прямой. |
|||||||
Рассмотрим на конкретных примерах методы решения задач, связанных непосредственно с |
|||||||
проектированием новой поверхности. |
|
|
|
|
|
|
|
Во всех случаях проектирования рельефа возникает необходимость нахождения точки с заданной |
|||||||
отметкой Нс на прямой, проходящей через точки А и В с известными отметками На и Нв. |
|||||||
Возможны несколько вариантов решения этой задачи: |
|
|
|
||||
а) графический способ: |
|
|
|
|
|
|
|
Дано : HА ,HВ ,HС . |
|
|
|
|
|
|
|
Найти :местоположение точки С на АВ (рис. 68) |
|
|
|
|
|
||
Рисунок 68 – Графический способ нахождения отметки точки |
|||||||

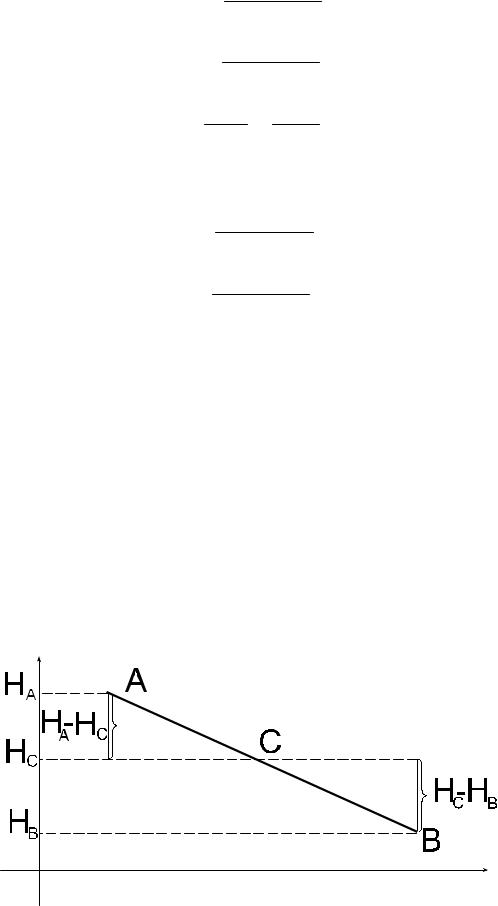
б) аналитический способ:
Дано: HА , HВ , lА-В
Найти: lА-С
|
lA−C |
= |
HC − HA |
|
|
lA−B |
|
HB − HA |
|
|
|
|
|
|
Рисунок 69 – Аналитический способ нахождения отметки точки
в) градуирование прямой (рис. 70):
Дано : HА, HВ , lА-В , h=0.2 м
Рисунок 70.
Определить: местоположение точек, соответствующих отметкам горизонталей при их сечении
h=0.2м (lА-1, l ,lN-B ).
Порядок вычислений:
∙ определение уклона линии А-В :
i= (HB − HA ) / lA−B;
∙вычисляют превышение между точкой А и ближайшей к ней большей по значению горизонталью, кратной высоте сечения рельефа h :
h1 = H1 − HA;
∙зная превышение и уклон, определяем величину заложения между точкой А и ближайшей к ней горизонталью:
lA−1 = h1 / i = (H1 − HA ) / i;
∙ находим заложение между точкой В и ближайшей горизонталью:
lN −B = (HB − HN ) / i;
HN - отметка кратной h ближайшей по значению к точке В меньшей горизонталью. ∙ определяем заложение между соседними горизонталями :
l = h / i;
h - сечение горизонталей или разность между соседними отметками.
∙откладываем по линии АВ полученные значения заложений с учетом масштаба плана, находим места горизонталей.