
геодезия конспект лекций
.pdfЗнаки "+","-" - характеризуют повышение или понижение рельефа.
4.Вычисляют рабочие отметки.
5.Строят проектные горизонтали.
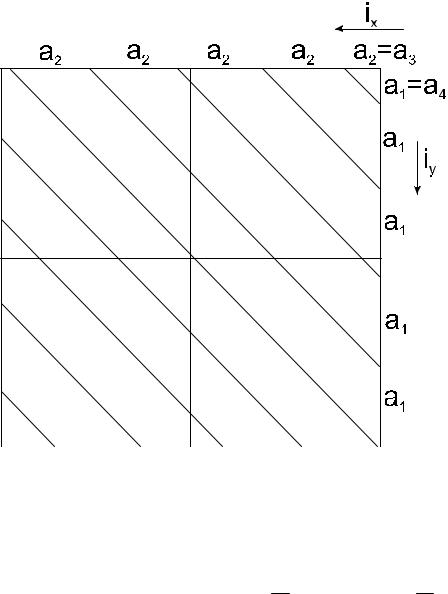
б) способ проектных горизонталей (рис. 86): |
|
|
|
|
|||
|
|
|
Рисунок 86. |
|
|
|
|
Дано: h -высота сечения рельефа; |
|
|
|
|
|
|
|
ix, iy - уклоны. |
|
|
|
|
|
|
|
Построить проектные горизонтали. |
|
|
|
|
|
|
|
- eсли H1 кратно высоте сечения рельефа h , то вычисляют: |
|||||||
a = |
h |
, |
a |
= |
h |
; |
|
1 |
i |
y |
|
2 |
|
i |
|
|
|
|
|
|
x |
|
|
- если H1 не кратно высоте сечения рельефа, то вычисляют не полные расстояния до первой от угла 1 горизонтали а3 и а4.
Например:
H1= 103,5 м; Нпр.1 = 103,6 м; h1 = Hпр.1 -H1.
a4 = h1 , a3 = h1 . iy ix
Вычисление проектных отметок вершин квадратов выполняются аналогично рассмотренной ранее методике.
1.2.9. Условные обозначения, используемые при составлении проекта вертикальной планировки

1.3. РАЗБИВОЧНЫЕ РАБОТЫ
1.3.1. Общие сведения о разбивочных работах
Разбивка запроектированных зданий или сооружений заключается в указании на местности их характерных точек и линий, по которым в процессе строительства при помощи простых приспособлений определяют положение всех частей зданий или сооружений. Способы
перенесения точек сооружений в натуру аналогичны способам определения положения точек при съемке (полярных и прямоугольных координат, прямой угловой засечки и т. п.).
Разбивка ведется с пунктов геодезической основы, созданной еще при съемке местности для проектирования или до начала строительства. Величины необходимых разбивочных элементов проекта (углов и длин линий) предварительно определяют графически или аналитически по проектному плану.
Выбор метода подготовки элементов проекта зависит от формы, размеров, материала, способа ведения строительных работ, определяющих вместе точность возведения сооружения. Разбивочный чертеж с указанием на нем необходимых данных (дирекционных углов, углов, длин линий, опорных и определяемых точек) подготавливают заранее и вычерчивают на чертежной бумаге, подшиваемой затем в специальные альбомы.
Способ разбивочных работ выбирают в зависимости от необходимой точности разбивки точки, наличия геодезических приборов; условий местности, способа ведения строительных работ, квалификации персонала и т. и. При этом различают метод непосредственной разбивки, состоящий в непосредственном построении разбивочных величин с заданной точностью, и метод редуцирования, основанный на предварительной разбивке точки, близкой к проектной, с последующим ее смещением в проектное положение. Метод непосредственной разбивки применяют, как правило, на работах меньшей точности, а метод редуцирования - на работах, требующих высокой точности разбивки (мостов, плотин и т. п.).
1.3.2.Способы разбивочных работ
1.3.2.1.Способ полярных координат
Для перенесения в натуру проектной точки P строят в опорном пункте A полярный угол β, откладывают расстояние S и фиксируют точку (рис. 87).
P
C
β
A 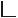

 B
B
Рисунок 87 - Способ полярных координат
Точность разбивки этой точки без учета погрешностей исходных данных определяют по формуле:
|
|
|
|
|
|
|||
|
m = ( |
S ×mβ |
)2 + m 2 + m 2 + m 2 + m 2 , |
|||||
|
r |
|||||||
|
P |
S |
e |
e1 |
ф |
|||
|
|
|||||||
где ms |
- средняя квадратическая погрешность отложения расстояния S; |
|||||||
mβ - средняя квадратическая погрешность построения угла b; |
||||||||
me ,me1 |
- средние квадратические смещения разбиваемой точки, обусловленные |
|||||||
соответственно неточностью центрирования теодолита и визирной марки на исходной стороне;
mф - средняя квадратическая погрешность фиксации разбиваемой точки.
При условии равного влияния погрешностей угловых и линейных измерений имеем:
|
mp ×r |
|
mp |
|
m |
mp |
|
mp |
|
|
m £ |
|
; m £ |
|
; |
S |
£ |
|
; m = m = m £ |
|
. |
1,5×S |
1,5 |
|
1,5×S |
5,22 |
||||||
β |
S |
|
S |
e e1 ф |
|
|||||
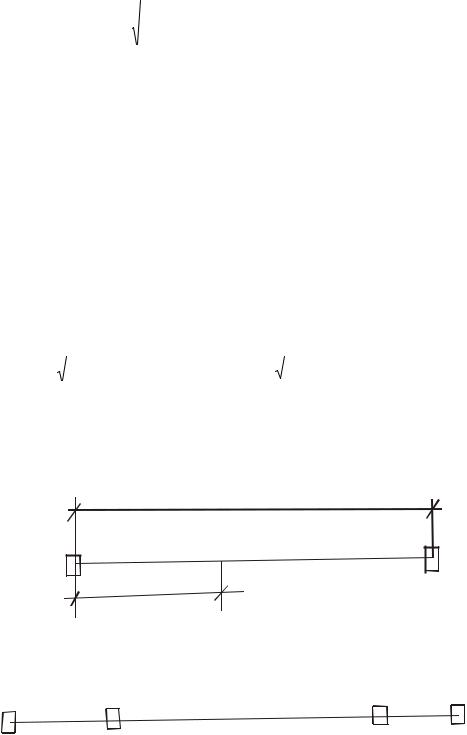
1.3.2.2. Способ створно-линейных координат Этот способ применяют в случае, если разбиваемая точка находится на опорной линии
между ее концами или на ее продолжении. Теодолит и визирную цель размещают на концах
опорной линии и по направлению визирования трубой теодолита откладывают проектное расстояние S и фиксируют точку C (рис. 88,а). Погрешность разбивки точки определяют по формуле:
|
|
|
|
|
|
|
|
|
|
|
m = m |
2 + m |
2 + m 2 |
; |
m = m 2 |
+ m |
2 + m |
2 + m 2 |
, |
||
C |
ств |
S |
ф |
|
ств |
e |
e1 |
виз |
u |
|
- погрешность створа;
mS - погрешность построения длины S; mф - погрешность фиксации точки; mu - СКО исходных пунктов;
mвиз - СКО фокусирования (визирования).
а) разбиваемая точка на опорной линии
b
A C B
S
Б)
S1
S2
b
A |
B |
C2 |
C1 |
|
|
Рисунок 88 – Способ створно-линейных координат |
|
|
Если разбиваемая точка находится на продолжении опорной линии (рис. 88,б), то створ задается либо поворотом трубы через зенит, либо построением угла в 180° (в обоих случаях при двух положениях круга и аналогично полярному способу). Более производительный и точный первый способ.
б) точка вне опорной линии.
Если точку P разбивают на продолжении створа AB, то погрешность построения самого створа возрастает пропорционально его длине, поэтому применять этот способ на большом протяжении не рекомендуется.

Пример. Требуется разбить точку P в створе линии строительной сетки длиной 200 м, имеющей предельную относительную погрешность 1: 10 000, на расстоянии 75 м при помощи теодолита типа Т-2 в комплекте с визирными марками, снабженными оптическими центрирами (линейные элементы центрировки и редукции e = e1 = 0.5 мм ), и мерного прибора, обеспечивающего измерение линии с погрешностью mS = 5мм.
В результате расчета получено:
|
|
|
m |
= |
|
|
|
l |
|
× b - S ; |
|
me=0,2 мм; |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
e |
|
|
|
|
2 |
|
|
|
|
S |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
m |
= |
|
|
|
l1 |
|
|
|
× |
S |
; |
|
me1=0,1 мм; |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
e1 |
2 |
|
|
b |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
m = |
3011 |
× |
|
2×S |
|
|
; |
|
|
m |
= |
30 |
11 × |
2×200000 |
|
= 1,6мм, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
виз |
v |
×r |
|
|
|
|
|
|
|
|
|
|
|
виз |
|
|
25×206265 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где b - длина створа;
30² - средняя разрешающая способность невооруженного глаза; v - увеличение зрительной трубы.
При фиксации точки с погрешностью mф = 0.5 мм получим:
mp = 
 0,22 + 0,12 + 16,2 + 5,02 + 0,52 = 6,1 мм.
0,22 + 0,12 + 16,2 + 5,02 + 0,52 = 6,1 мм.
Здесь влияние отложения длины оказалось доминирующим.
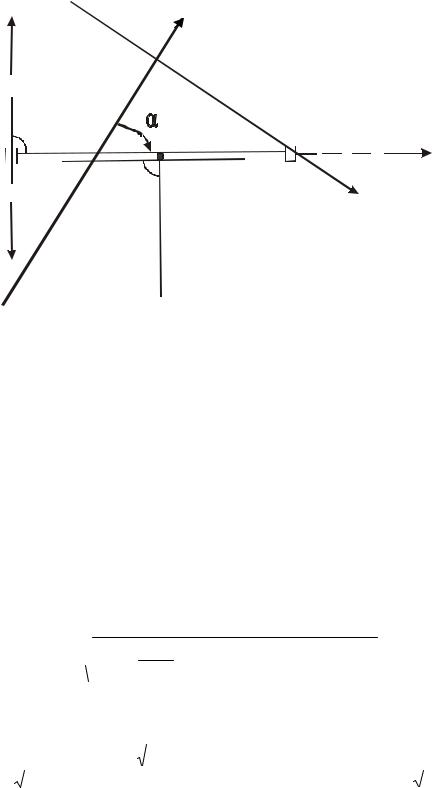
1.3.2.3. Способ прямоугольных координат
В основу способа положена разбивка проектной точки P от линии геодезической основы AB, чаще - от линии строительной сетки, полигонометрии или теодолитного хода (рис. 89) по прямоугольным координатам x и y относительно точки A, взятой за начало частной системы координат, и линии AB - в качестве частной оси абсцисс.
-Y |
X |
A |
|
|
X |
0C |
|
||
|
|
|
|
|
|
|
|
|
|
|
B |
||||
|
|
|
|
||||
|
|
|
|
|
|||
Y
Y
Y
 P
P
Рисунок 89 - Разбивка точки способом прямоугольных координат
Прямоугольные координаты определяют по формулам:
x= ( X P - X A )×cosa0 + (YP - YA )×sina0 ;
y= (YP - YA )×cosa0 -( X P - X A )×sina0 ,
где XA , XP , YA ,YP - абсолютные координаты исходной и проектной точек; a0 - дирекционный угол опорной линии AB.
Знаки ординат указывают направление откладывания их от створных точек линии AB: при положительной - вправо, при отрицательной - влево. Если абсцисса x отрицательная, то ее откладывают от точки A в противоположном направлении линии AB.
Для разбивки точки теодолит устанавливают в пункте А и ориентируют по линии AB при помощи визирной цели, установленной в пункте B. Затем вдоль линии визирования откладывают расстояние x и фиксируют створную точку C. Устанавливают в ней теодолит, строят прямой угол при двух положениях круга с выбором средней точки и, отложив ординату y , фиксируют проектную точку P.
Среднюю квадратическую погрешность точки P определяют по формуле: mP = 
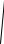 mx 2 + ( y ×rmρ )2 + 2×(me2 + me12 + mф2 ) + my 2 .
mx 2 + ( y ×rmρ )2 + 2×(me2 + me12 + mф2 ) + my 2 .
Здесь в скобки заключены погрешности установок и фиксации, влияние которых невелико. Поэтому, применив к отдельным членам подкоренного выражения принцип комбинированного влияния (равного и неравного в зависимости от величины составляющих), получим:
m = |
|
mp |
; T ³ |
|
x2 + y2 |
; |
m £ |
mp |
; m |
= m |
= m £ |
m |
|
, |
|
|
|
|
|
|
|
|
|
||||||||
|
|
2×v2 +1 |
|
|
m |
|
|
y |
e |
e1 |
ф |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где T - знаменатель предельной относительной погрешности линейных измерений при откладывании расстояний;
m - некоторая вспомогательная погрешность;
v - коэффициент соотношения погрешностей, принимаемый в зависимости от имеющихся инструментов и условий производства работ (обычно v = 2, 2.5 или 3).
Пример. Определить, с какой погрешностью следует производить разбивку проектной точки с прямоугольными координатами x = 80 м и y = 60 м, если ее среднее квадратическое отклонение от проекта не должно превышать mр = 25 мм.
Приняв v = 2, получим T ³ 3 000; mβ < 57² ; me = me1 = mф = 3.4 мм. По этим данным выбирают приборы для производства работ: теодолит 30² точности, рулетку, тонкую веха. Приборы центрируют средним нитяным отвесом, точки фиксируют шпилькой на колышке. 1.3.2.4. Способ полярно- прямоугольных координат Этот способ является модификацией способа прямоугольных координат с той лишь разницей,
что координаты строят на вспомогательной линии AB', составляющей угол j с линией геодезической основы AB.
Например, по условиям строительства необходимо разбить ряд точек P1, P2 , ..., Pn ,
находящихся на одной прямой или нескольких параллельных прямых с заданным дирекционным углом a (рис. 90). При известных дирекционных углах a и a0 направлений AB и AB' определяют угол j = a - a0 . Откладывая его от направления AB, строят вспомогательную линию AB'. Она является базовой для построения прямоугольных координат x и y пунктов застройки, найденных по формулам:
x= ( X p - X A )×cosα0 + (Yp - YA )×sinα0
y= (Yp - YA )×cosα0 + ( X p - X A )×sinα0
сиспользованием дирекционного угла a линии AB'.
X B
0 |
Y |
ϕ= 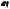
 -
-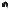
 0
0
A 

|
|
X1 |
|
|
X2 |
|
X3 |
|
X4 |
B‘, |
X |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y1 |
|
Y2 |
|
Y 3 |
|
Y 4 |
|
|
|||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
P1 |
|
|
P2 P3 |
|
|
|
|
P4 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y 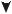
Рисунок 90 - Способ полярно-прямоугольных координат Применение способа полярно-прямоугольных координат позволяет сократить длины ординат и
создать лучшие условия для разбивочных работ. Точность разбивки определяют по формуле:
|
|
|
|
|
|
|
m = m |
2 + ( |
y×mβ |
)2 + 2×( m 2 + m 2 + m 2 ) + m 2 |
|||
ρ |
||||||
p |
x |
|
e e1 ф |
y |
||
|
|
|||||
с учетом погрешности разворота линии АВ¢, выраженной зависимостью:
( mp )AB1 = 
 x2 + y2 × mρϕ ,
x2 + y2 × mρϕ ,
где mϕ - погрешность построения угла j.
1.3.2.5. Способ прямой угловой засечки Этот способ применяется для разбивки удаленных и труднодоступных объектов - мостовых
переходов и гидротехнических сооружений. При этом, положение проектной точки P с известными координатами определяют в натуре путем построения двух проектных углов β1 и β2 соответственно в двух твердых пунктах A и B (рис. 91).
|
|
|
P |
||
|
S3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
||
4 |
S2 |
2 |
1 |
|
|
|
|
|
|||
C |
3 |
|
|
|
|
|
|
|
|
|
|
b |
|
2 |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
A |
|
B |
|
|
|
|
|
|
|
|
||
|
|
b1 |
|||
Рисунок 91 - Прямая угловая засечка
На точность разбивки влияют следующие источники: погрешность собственно прямой засечки и погрешность, обусловленная неточностью фиксации линий засечки (более подробно рассмотрено в вопросе мостовой триангуляции).
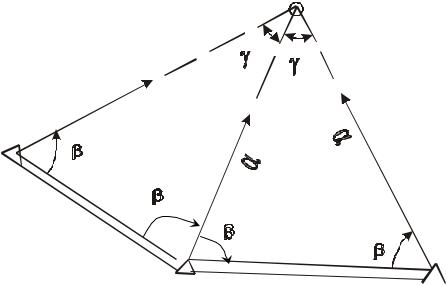
1.3.2.6. Способ замкнутого треугольника Способ используется для уточнения положения точки, разбиваемой прямой угловой засечкой,
главным образом при отсутствии дополнительных опорных пунктов.
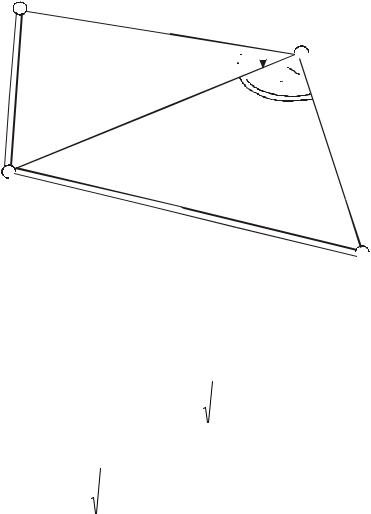
Теодолит устанавливают в найденной точке и измеряют третий угол треугольника. Распределив невязку поровну или в соответствии с весами измеренных углов, определяют координаты точки Р (рис. 92). Сравнив их с проектными, находят поправки - редукции, на которые смещают первоначально найденную точку в проектное положение.
3
S3
P
 1
1 


 2
2 
S2 
 3
3
S1
2
b
 1
1
Рисунок 92 - Вставка точки в треугольник
Для оценки точности ее определения применяют формулу Ф. Красовского (без учета исходных данных).
mP = |
mβ |
|
S12 + S22 + b2 |
. |
ρ sinγ |
3 |
|||
При разбивке точки с трех пунктов (при вставке точки в треугольник) применяют формулу проф. К.Л. Проворова :
mP = |
mβ |
|
(S1S2 )2 + (S1S3 )2 + (S2S3 )2 |
|
|
, |
||||||||||
ρ |
|
|
(S |
sinγ |
1 |
)2 + (S |
2 |
sinγ |
2 |
)2 + (S |
3 |
sinγ |
3 |
)2 |
||
|
1 |
|
|
|
|
|
|
|
||||||||
где γ 1 ,γ 2 ,γ 3 - углы засечки соответственно между визирными лучами 2 и 3, 1 и 3, 1 и 2;
S1 ,S2 ,S3 - длины визирных лучей с пунктов 1, 2, 3.
1.3.2.7. Способ линейной засечки
Способ применяется, в основном, для разбивки точек сооружений по расстояниям S1 и S2, которые не превышают длины мерных приборов. Свето-, радио- и оптические дальномеры целесообразно применять по методу редуцирования. Разбивка состоит в нахождении точки пересечения дуг, построенных мерными приборами длиной S1 и S2, поэтому ее можно осуществлять двумя или поочередно одним мерным прибором (рис. 93).
