геодезия конспект лекций
.pdf
координаты двух пунктов X1 ,X2, Y1 ,Y2 в государственной системе и x1 , x2 , y1 , y2, в строительной, элементы формул находят из выражений:
( x - x )×(Y - Y )- ( y - y )×( X - X )
v × sinq = 1 2 1 2 2 1 2 2 1 2 ;
( x1 - x2 ) + ( y1 - y2 )
v ×cosq = ( x1 - x2 )×( X1 - X2 ) - ( y1 - y2 )×(Y1 -Y2 ) ; ( x1 - x2 )2 + ( y1 - y2 )2
a = X1 - x1×cosq + y1×v×sinq;
b= Y1 - x1×v×sinq - y1×v×cosq.
Вслучае необходимости осуществляют переход от координат пунктов в
государственной системе к координатам в строительной системе по формулам:
x= ( X - a )×cosq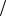
v - ( y - b)×sinq
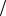v ;
y= ( X - a )×sinq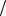
v + ( y - b)×cosq
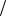v .
Причем, величины cosq/v и sinq/v находят по известным значениям v×cosq и v×sinq:
sinq |
= |
|
v ×sinq |
; |
||
v |
|
(v ×sinq)2 + (v ×cosq)2 |
||||
cosq |
= |
|
v ×cosq |
|
; |
|
v |
|
(v × sinq )2 + (v ×cosq)2 |
|
|||
или вычисляют по формулам:
sinq |
|
= |
( x1 - x2 )×(Y1 - Y2 ) - ( y1 - y2 )×( X1 - X2 ) |
|
; |
||||||||
v |
|
|
|||||||||||
|
|
( X |
1 |
- X |
2 |
)2 + (Y - Y )2 |
|
||||||
|
|
|
|
|
|
1 |
2 |
|
|
||||
cosq |
= |
|
( x1 - x2 )×( X1 - X2 ) - ( y1 - y2 )×(Y1 - Y2 ) |
. |
|||||||||
v |
|
||||||||||||
|
|
( X |
1 |
- X |
2 |
)2 + (Y - Y )2 |
|
||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
||
Для упрощения вычислений целесообразно при возможности совмещать начало координат строительной сетки с пунктом, координаты которого известны. в государственной (местной)
системе, и измерять с него примычной угол на смежный пункт государственной геодезической сети. Пункты, используемые для перевычисления координат, целесообразно располагать на одной линии сетки, так как в этом случае в формулах, служащих для нахождения v×cosq и v×sinq, обращаются в нуль по одному члену в числителе и знаменателе.
1.1.4.8. Определение высот пунктов строительной сетки
Строительная сетка промышленных площадок служит высотной основой выноса в натуру проекта сооружения и производства исполнительных съемок. При
установке точек по высоте в процессе монтажных работ горизонт инструмента должен (для контроля) определяться не менее чем от двух реперов, причем расхождение не должно превышать 3 - 4 мм, поэтому точности взаимного определения высот соседних реперов в среднем не должна превышать ±2 мм. Из исследований было выявлено, что при такой точности высоты пунктов строительной сетки должны быть определены из нивелирования III класса.
RP1
RP2 
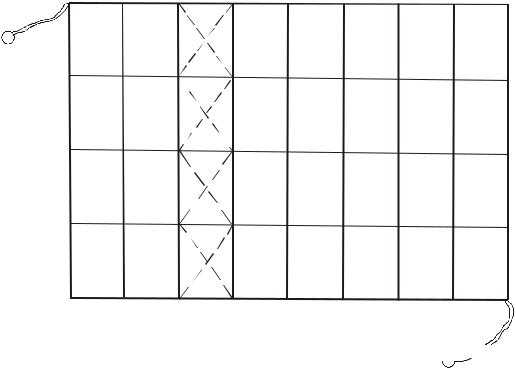
Рисунок 47 - Высотное обоснование строительной сетки Как правило, нивелировку прокладывают по контуру строительной сетки, а
затем делят на полигоны ходами, параллельными одной из осей строительной системы координат (выбирают более короткие стороны). На рис.47 двойными линиями показано расположение нивелирных ходов III класса на строительной сетке. Для обеспечения увязки высотной сети с соседними объектами
осуществляют привязку строительной сетки не менее чем к двум реперам государственной нивелирной сети (на рис. 4. это Rp1 и Rp2). Однако чтобы не
вносить в жесткую разбивочную сеть ошибок исходных данных, ее отметки вычисляют только от одного репера, а второй служит для контроля.
Поскольку при нивелировании III класса нормальная длина визирного луча составляет 75м, при построении сеток с длинами сторон квадратов 100 м можно повысить производительность труда, располагая станции на пересечении диагоналей квадратов. Передвигаясь по этим точкам I1 ,I2 ,I3 ... (см. рис.47), можно одновременно нивелировать два хода.
Нивелировку уравнивают обычно по способу полигонов. На больших сетках
для математической обработки нивелирования может оказаться целесообразным использование ЭВМ.
1.1.4.9. Методы построения сетей второго порядка
1.1.4.9.1.Полигонометрия
Полигонометрию 2-го порядка строят в виде вытянутых ходов (в случае сетки из одинаковых прямоугольников или квадратов - с равными сторонами), опирающихся на пункты полигонометрии 1-го порядка и прокладываемых по кратчайшему расстоянию между ними. Недостатком полигонометрии является отсутствие взаимной связи между соседними ходами. Поэтому, учитывая
важность обеспечения достаточной точности взаимного положения соседних пунктов, следует несколько завышать точность измерений по сравнению с получаемой из расчетов на допуски разбивочных работ и исполнительных съемок. Это относится и к любым другим методам, при применении которых пункты внутри каркаса получают из отдельных взаимно не связанных построений.
Исходя из полученной средней квадратической ошибки ±4.1 см положения пункта, находящегося в середине хода 2-го порядка, получим средний линейный сдвиг в конце хода ±9 см, и предельно допустимую абсолютную невязку хода ± 18 см. При длине хода 1 - 1,5 км это приведет к предельной относительной невязке хода 1: 6 000 - 1: 10 00. Учитывая сказанное выше, не следует прокладывать ходы 2-го порядка с предельной относительной ошибкой более 1: 10 000.
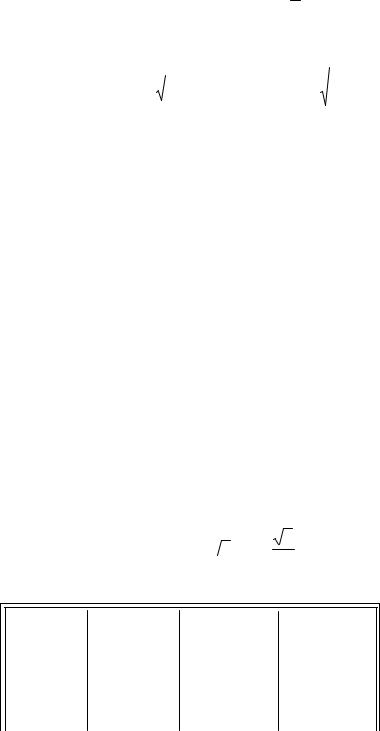
Поскольку сети 2-го порядка служат для определения координат основной массы пунктов строительной сетки, при построении которой одинаково нежелательны деформации как в продольном, так и в поперечном направлении, расчет необходимой точности измерений в полигонометрии выполняют, исходя из принципа равных влияний продольных и поперечных ошибок, т. е. полагая, что ошибка положения пункта равна:
M2 = mt2 +mu2 ,
где mt , mu - соответственно продольная и поперечная ошибки. Следует принять:
mt = mu =M× 
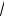2 .
Сдвиг конечной точки вытянутого хода вычисляют по формулам:
mt = |
|
; mu = |
mB |
× L × |
|
n + 3 |
|
. |
|
[mS 2 ] |
|||||||||
|
12 |
||||||||
|
|
|
r |
|
|
||||
Средняя квадратическая ошибка в определении положения пункта в середине вытянутого хода полигонометрии между пунктами каркасной полигонометрии, равна:
mc = M/2≤ 4.1 мм,
где M- ошибка положения пункта в конце хода , она вычисляется для хода АВ по формулам:
M 2 |
= m 2 |
×n× |
mβ |
2 |
+ |
n + 3 |
× L2 - для ×вытянутого× хода |
|||
r2 |
|
|||||||||
|
S |
|
|
12 |
|
|||||
|
|
|
|
|
|
2 |
×[DЦТ |
2 ]- для ×изогнутого× хода |
||
M 2 |
= mS |
2 |
×n + |
mβ |
|
|||||
2 |
|
|||||||||
|
|
|
|
|
r |
|
|
|
|
|
где n -число сторон хода;
[DЦТ2] - сумма квадратов расстояний от центра тяжести до текущих точек. Средняя квадратическая ошибка взаимного положения пунктов CD (рис.48):
2
mCD = mC × 
2 = M × 2 £ 18мм.
B
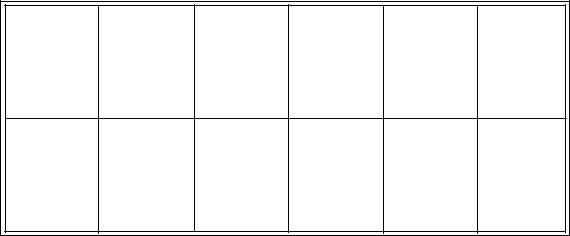
C D
A
Рисунок 48.
1.1.4.9.2. Метод четырехугольников без диагоналей
Сети четырехугольников без диагоналей, заполняя каркас, создают сплошную сеть (рис.49). Все пункты этой сети взаимно связаны и своей формой эта сеть напоминает строительную сетку. Так как диагональные направления не измеряются, то этот метод с успехом используется на застроенных и залесенных площадках.
Рисунок 49 – Схема построения четырехугольников без диагоналей
|
При расчете точности измерений в |
сети, |
уравненной |
между пунктами |
||||||
каркаса, можно использовать таблицу 7. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Таблица 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Система |
Q |
QSx |
|
Qαx |
|
QSy |
|
Qαy |
|
|
построения |
|
|
|
|
|
|
|
|
|
|
Sx = Sy |
|
|
|
|
|
|
|
|
|
|
3x3 |
0,59 |
0,60 |
|
0,41 |
|
0,59 |
|
0,41 |
|
|
3x4 |
0,67 |
0,76 |
|
0,41 |
|
0,59 |
|
0,44 |
|
|
3x5 |
0,71 |
0,84 |
|
0,41 |
|
0,59 |
|
0,46 |
|
4x3 |
0,76 |
0,59 |
0,44 |
0,72 |
0,41 |
4x4 |
0,67 |
0,76 |
0,45 |
0,76 |
0,45 |
4x5 |
0,81 |
0,84 |
0,45 |
0,77 |
0,47 |
5x3 |
0,71 |
0,59 |
0,46 |
0,84 |
0,41 |
5x4 |
0,81 |
0,77 |
0,47 |
0,84 |
0,45 |
5x5 |
0,86 |
0,86 |
0,47 |
0,86 |
0,47 |
Нормированные обратные веса вычислены для наиболее слабых элементов сети, независимо от конкретной длины ее сторон. При этом приняты следующие обозначения:
Q -корень из нормированного обратного веса положения пункта в самом слабом месте сети;
QSx , QSy - то же - для длин соответствующих сторон; Qαx , Qαy - то же - для дирекционных углов этих сторон.
Переход к сети с конкретными |
длинами сторон осуществляется по |
|||||||||
формулам: |
|
|
|
|
|
|
|
|
|
|
mα( Sx ) = |
|
|
mS2 |
; |
mα( Sy ) = |
|
mS2 |
; |
||
|
K1 ×QSx |
K1 ×QSy |
||||||||
m |
= |
mα2 |
; |
|
m |
= |
mα2 |
; |
|
|
|
|
|
|
|||||||
α( αx ) |
|
|
Qαx |
|
α( αy ) |
|
Qαy |
|
||
|
|
|
|
|
|
|
||||
где mS2 и mα2 - требуемая точность длин сторон и дирекционных углов этих сторон.
В заполняющих сетях mS=10 мм, mα=10².
Из этих четырех значений выбирают минимальное и вычисляют ошибку положения пункта:
MII =K1× mα(min)× Q, K1 =S/r";
где S - длина стороны строительной сетки в мм.
1.1.4.9.3. Микротриангуляция
Микротриангуляцию строят для определения координат пунктов строительной сетки из цепочек между исходными сторонами полигонометрии 1-го порядка (риc. 50). В результате получают взаимосвязанные элементы двух рядов пунктов сетки. Недостаток метода
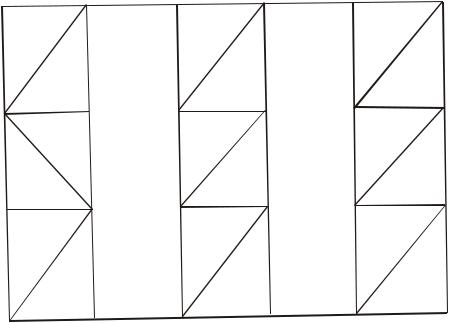
заключается в том, что отсутствует взаимная связь между смежными цепочками. Поскольку обычно все цепочки имеют одинаковую протяженность и форму, при составлении проекта достаточно рассчитать требуемую точность измерений один раз.
Рисунок 50 – Схема построения цепочек микротриангуляции
Угловые измерения в сети выполняют по трех штативной системе. Для
расчета их точности и оценки точности уравненных элементов сети можно использовать табл. 8 (по аналогии с табл. 7) .
|
|
|
|
|
|
|
|
Таблица 8 |
|
|
|
|
|
|
|
|
|
|
|
Система |
Число |
Q |
QSx |
Qαx |
QSy |
Qαy |
QS |
Qα |
|
построения |
треугольн |
|
|
|
|
|
|
|
|
|
иков |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sx = Sy |
6 |
1,1 |
0,94 |
0,66 |
0,72 |
0,61 |
0,9 |
1,3 |
|
|
8 |
1,5 |
1,0 |
0,78 |
0,80 |
0,65 |
1,3 |
1,7 |
|
|
10 |
1,8 |
1,1 |
0,82 |
0,84 |
0,72 |
1,6 |
2,0 |
|
|
|
|
|
|
|
|
|
|
|
Sx = Sy/ 2 |
6 |
1,4 |
1,4 |
0,66 |
0,84 |
1,2 |
1,0 |
1,8 |
|
|
8 |
1,5 |
1,5 |
0,80 |
1,0 |
1,3 |
1,5 |
2,1 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
1,6 |
1,6 |
0,80 |
|
1,1 |
1,4 |
|
1,7 |
|
2,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Примечание |
: QS |
и Q |
α - корни из нормированных обратных весов длины и |
||||||||||
дирекционного угла стороны между пунктами соседних цепочек в их середине. |
|||||||||||||
Рассмотрим примеры расчета точности сети, |
принимая, |
как и |
в примерах |
||||||||||
для метода четырехугольников без диагоналей, те же исходные данные. |
|
|
|
||||||||||
Пример 1. Число треугольников n=10, сетка квадратов S1 = S2=S= 200 м, mS2
=±10 мм, ma2 =±10", M=±40 мм, К1 =0.97.
Для обеспечения требуемой точности определения длин сторон имеем:
mα( Sx ) = |
|
mS |
|
|
10 |
= ±9,4 |
²; |
mα( Sy ) = |
|
|
|
mS |
|
|
|
|
10 |
|
= ±12 |
²; |
||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|||||||||||||
|
K1 ×QSx |
0,97 ×1,1 |
|
K1 ×QSy |
0,97 ×0,84 |
|||||||||||||||||||||||
|
m |
= |
|
|
mα |
= |
10 |
= ±12 ²; |
|
m |
= |
mα |
= |
10 |
= ±14 ²; |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
α( αx ) |
|
|
Qαx 0,82 |
|
|
α( αy ) |
|
|
Qαy |
0,72 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
m = |
mS |
|
= 10 = ±5 ²; |
m = |
mS |
|
= |
|
|
10 |
|
|
= ±6,4 ²; |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
α |
Qα |
2,0 |
|
|
|
S |
|
K1 ×QS |
|
|
|
0,97 ×1,6 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Приняв за окончательный более жесткий допуск |
|
mα (min) = ± 5" получим |
||||||||||||||||||||||||||
ошибку положения пункта:
M = K1×mα(min)×Q = 0,97×5×1,8 = ±8,7 мм.
При уравнивании цепочки микротриангуляции между сторонами полигонометрии 1-го порядка применяют коррелатный способ. Отнеся в первую группу условия фигур и введя первичные поправки путем распределения невязок поровну, для нахождения вторичных поправок решают систему из четырех нормальных уравнений коррелат, соответствующих условиям базиса, дирекционных углов, абсцисс и ординат. Свободные члены этой системы находят по первично исправленным углам.
1.1.4.9.4. Метод геодезических засечек
На открытых площадках сети 2-го порядка могут быть построены методом геодезических засечек. На строительных сетках применяют двух фигурные засечки с двусторонним расположением вспомогательных пунктов. Сеть строят из отдельных цепочек (рис. 51, а, б),
что позволяет взаимно увязать по три ряда пунктов и в то же время сократить число станций,
на которых ведут измерения, приблизительно в три раза. Иногда создают сплошную сеть
(рис. 52), при которой число станций соответствует примерно половине пунктов сети 2-го порядка, но зато все вершины сетки взаимно увязаны.
а) |
б) |
B2
B2 
B1
B1
Рисунок 51
Рисунок 52 – Схема сплошной сети в виде цепочки геодезических засечек
Измерение углов на пунктах ходовой линии должно выполняться с особой тщательностью,
так как приходится на каждом пункте наблюдать восемь направлений, что затягивает прием.
При плохой видимости рекомендуется разбивать прием на две серии, включая в каждую два направления по ходовой линии и все направления по одну ее сторону.
Обычно переход от сети первого порядка к цепочке засечек осуществляют построением в местах примыкания сплошных треугольников (см. рис. 51, а; рис. 52). Иногда (см. рис. 51,б),
измеряют крайние стороны ходовой линии в качестве базисов и передают на них дирекционные углы с пунктов первого порядка. Последний случай может оказаться более эффективным, когда стороны сети первого порядка измеряют светодальномером.
При проектировании сети и оценке точности ее элементов после уравнивания используют формулы: