
геодезия конспект лекций
.pdf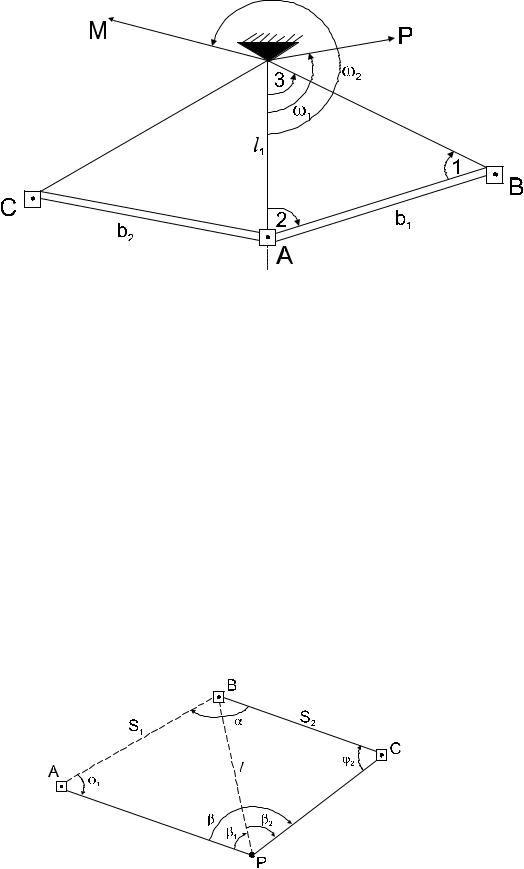
Рисунок 26 - Передача координат со здания на грунтовый пункт
полигонометрического хода Также измеряют углы 1, 2, 3, ω1, ω2. Затем вычисляют l1:
l1 |
|
= |
b1 |
|
; |
|
sin1 |
sin 3 |
|||||
|
|
|||||
αО-А=αО-Р + ω1.
Затем вычисляют координаты XА и YА
1.1.2.4.Измерение углов и длин при отсутствии видимости между точками
1. Измерение углов. Между точками А и В отсутствует видимость. Для вычисления угла α выбираем вспомогательную точку Р, на которую есть видимость с точек А и С и измеряем β1, β2, β, l=BP.
Рисунок 27. Затем вычисляем:
α = 360° - (ϕ1 + ϕ2 + β);

sinϕ1 = (l× sinβ1)/ S1; sinϕ2 = (l× sinβ2)/ S2
2. Измерение длин.
1)Между точками А и В есть препятствие, но видимость есть. Выбирают точку С
иизмеряют S1, S2, α, β. Затем вычисляют расстояние по формуле:
AB= AC×cos α + BC×cosβ.
2) Между точками А и В есть препятствие и нет видимости.
Так как видимость отсутствует, следовательно вместо угла β необходимо измерить угол θ, тогда:
AB2 = AC2 +BC2 - 2×AC×BC×cosθ.
Рисунок 28.
1.1.2.5. Метод редукции при линейных измерениях
Метод редукции при линейных измерениях иногда применяют в городской полигонометрии, т.к. он позволяет отойти от линии на местности, явно неблагоприятной для измерения (посевы, котлованы, каналы, сильное движение и т.д.) и перейти к линиям , удобной для измерения.
Следует различать три типа редукции: линейная, комбинированная, угловая.
1. Линейная редукция.
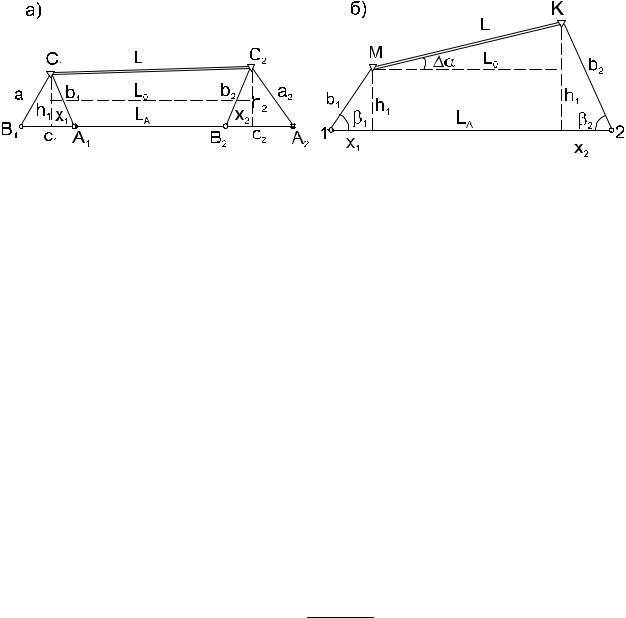
Рисунок 30 - Линейная (а) и комбинированная (б) редукции расстояний.
Здесь точки С1,C2 - центры геодезических пунктов, между которыми необходимо определить расстояние; - А1А2 вспомогательная линия, измеряемая
мерным прибором на местности; точки В1, В2 − располагают |
строго |
по створу |
||
вспомогательной линии. Кроме |
вспомогательной |
линии |
на |
местности |
измеряют рулеткой отрезки |
а1, а2 , в1, в2, с1, с2 . |
|
|
|
Точки А1А2 , В1, В2 − выбираются по створу измеряемой линии таким образом,
чтобы получились равнобедренные треугольники с углами при точках С1,C2 от 50
до 90 градусов.
Элементы линейной редукции вычисляют по формулам
x = [(b12 − a12 ) / c1 + c1 ]/ 2;
h = 
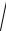 b12 − x12 ;
b12 − x12 ;
Искомое расстояние :
L = Lo + |
h2 |
; |
|
2Lo |
|
L0 = LA + x1 + x2 ; h = h1 ± h2.
В формуле знак “+” ставится, если построенные редукционные треугольники находятся по разные стороны измеряемой линии, и знак “-” - треугольники по одну сторону измеряемой линии (рис. 30, а).
2. Комбинированная редукция |
|
Комбинированную редукцию применяют , если |
отсутствует прямая |
видимость между постоянными геодезическими пунктами М и К (рис. 30,б). На местности выбирают вспомогательную линию 1-2, удобную для измерения.
Помимо линии 1-2 измеряют в точках 1 и 2 угловые β1, β2 и линейные в1,в2
элементы редукции с точностью соответствующего класса измерений. Вычисления выполняют по следующим формулам:
h1 = b1 sin β1; h2 = b2 sin β2; x1 = b1 cosβ1; x2 = b2 cos β2;
L0 = LA − x1 − x2; tg α = (h1 ± h2 ) / L0;
L = L0 sec α.
Редукция угловая занимает очень много времени и применяется в тех случаях, когда по каким-либо причинам линейный элемент редукции определить не возможно.
1.1.3. Геодезические разбивочные опорные сети
1.1.3.1. Общие сведения
Геодезические опорные разбивочные сети служат основой для выноса проектов сооружения в натуру, соблюдения их геометрических параметров,
производства геодезических наблюдений за смещениями и деформациями инженерных сооружений. Они создаются на строительной площадке в виде
развитой сети закрепленных знаками пунктов и обеспечивают исходными данными последующие построения на всех этапах строительства и эксплуатации сооружений.
Геодезическую разбивочную основу увязывают с имеющимися в районе строительства пунктами государственной сети или геодезических сетей сгущения, а также пунктами периода ранее проведенных инженерных изысканий. Проект
разбивочной основы составляется в соответствии с генеральным планом объекта строительства в порядке и в сроки, соответствующие принятым стадиям проектирования и очередям строительства. Точность построения геодезической разбивочной основы должна соответствовать требованиям табл.5. (СНиП 3.01.0384. Геодезические работы в строительстве. М., Стройиздат,1984).
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Допустимые средние квадратические |
|||||
Класс |
|
Объекты строительства |
|
|
|
|
погрешности |
|
||||||
точно |
|
|
|
|
|
|
|
|
угловые |
|
линейные |
|
отметки, |
|
сти |
|
|
|
|
|
|
|
|
величины, |
|
измерения |
|
мм |
|
|
|
|
|
|
|
|
|
|
сек |
|
|
|
|
|
1-0 |
Предприятия и группы зданий |
|
|
|
|
|
|
|||||||
|
и |
сооружений |
на |
участках |
|
|
|
|
|
|
||||
|
площадью |
|
более |
100 |
га. |
5 |
|
1:50 000 |
|
2 |
|
|||
|
Отдельно |
стоящие |
здания |
и |
|
|
|
|
|
|
||||
|
сооружения |
с |
|
площадью |
|
|
|
|
|
|
||||
|
застройки более 100 тыс. кв. м. |
|
|
|
|
|
|
|||||||
2-0 |
Предприятия и группы зданий |
|
|
|
|
|
|
|||||||
|
и |
сооружений |
на |
участках |
|
|
|
|
|
|
||||
|
площадью до 100 га. Отдельно |
10 |
|
1:15 000 |
|
2 |
|
|||||||
|
стоящие здания и сооружения с |
|
|
|
|
|
|
|||||||
|
площадью застройки свыше 10 |
|
|
|
|
|
|
|||||||
|
до 100 тыс. кв. м. |
|
|
|
|
|
|
|
|
|
|
|||
3-0 |
Здания |
и |
сооружения |
|
с |
|
|
|
|
|
|
|||
|
площадью застройки до 10 тыс. |
|
|
|
|
|
|
|||||||
|
кв. м |
|
|
|
|
|
|
20 |
|
1:5 000 |
|
3 |
|
|
|
Дороги, |
|
подземные |
|
и |
|
|
|
|
|
|
|||
|
надземные |
коммуникации |
|
в |
|
|
|
|
|
|
||||
|
пределах |
|
застраиваемых |
|
|
|
|
|
|
|||||
|
территорий |
|
|
|
|
|
|
|
|
|
|
|
||
4-0 |
Дороги, |
|
подземные |
|
и |
|
|
|
|
|
|
|||
|
надземные |
коммуникации |
вне |
30 |
|
1:2 000 |
|
5 |
|
|||||
|
застраиваемой территории |
|
|
|
|
|
|
|
|
|||||
|
Класс точности |
построения |
геодезической |
разбивочной |
основы особо |
|||||||||
сложных и уникальных инженерных сооружений, а также зданий выше 16 этажей
устанавливают при разработке проекта производства геодезических работ (ППГР). Точность измерения базиса геодезической разбивочной основы определяется специальными расчетами.
Геодезическую разбивочную основу создает заказчик и не менее чем за 10 дней до начала строительно-монтажных работ передает подрядчику
техническую документацию на нее и на закрепленные на площадке строительства пункты и знаки основы. Знаки геодезической разбивочной основы в процессе строительства находятся под наблюдением за их сохранностью и устойчивостью.
Положение знаков проверяет строительная организация не реже двух раз в год или в сроки, установленные в ППГР.
В районах крупного строительства и на городских территориях создается высотная основа для инженерно-геодезических разбивочных работ и наблюдений за осадками в виде нивелирных сетей II и III классов. Ходы нивелирования IV класса развивают по необходимости. При строительстве уникальных и крупных инженерных сооружений, для монтажа и наблюдения за осадками создают локальные специальные опорные высотные инженерно-геодезические сети высокой точности.
Необходимость создания высокоточных высотных опорных геодезических сетей обосновывается в ППГР. Методику и точность производства геодезических
измерений выбирают на основе расчетов точности и оценки качества проектов нивелирных сетей. Нивелирные ходы таких сетей прокладывают в прямом и обратном направлениях или при двух горизонтах инструмента.
Для высокоточного нивелирования применяют нивелиры Н1, Н2, Ni004, Ni007, Ni-B3 и др. Рейки - штриховые с инварной полосой. Нивелиры и рейки подвергают тщательным исследованиям по полной программе.
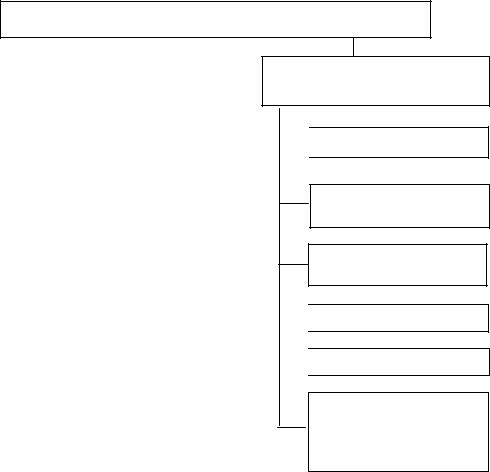
Опорные геодезические разбивочные сети
Расположенные в районе площ
|
|
|
|
|
|
|
|
|
Государственные |
||||
строительства |
|
геодезические сети: |
||||
|
триангуляции, |
|||||
|
|
|||||
|
|
трилатерации, |
||||
|
|
полигонометрии I и II |
||||
|
|
классов, нивелирование I и |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сети сгущения: |
|
||
|
|
|
триангуляция, |
|
||
|
|
|
трилатерация III и IV кл., |
|
||
|
|
|
полигонометрия III и IV |
|
||
|
|
|
кл., 1, 2 разрядов, |
|
||
|
|
|
нивелирование III и IV |
|
||
|
|
|
|
|
|
|
|
|
|
|
Съемочное обоснование |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Специальные сети, построенные
для разбивочных работ

 Мостовая триангуляция
Мостовая триангуляция
Тоннельная триангуляция (сторона
Микротрилатерация (сторона 20-50 м)
 Строительная сетка
Строительная сетка

 Красная линия
Красная линия
Линейно-угловые построения (засечки,
четырехугольники без диагоналей и т.д. )
Рисунок 31 – Классификация опорных геодезических разбивочных сетей
Выбор вида построения опорных разбивочных геодезических сетей зависит от следующих факторов:
-типа объекта; -его формы и площади; -его назначения;
-физико-географических условий района строительства; -точности; -наличия измерительных средств у исполнителя ; и др.
Например, триангуляция применима для значительных площадей, особенно для вытянутых объектов: мостов, гидротехнических сооружений и т.д.
Полигонометрия применима для застроенных территорий и дорожного строительства.
Линейно-угловые сети применяются при строительстве уникальных сооружений, где требуется высокая точность.
Строительная сетка применяется при строительстве крупных промышленных комплексов.
Теодолитные ходы применяются при строительстве отдельных зданий небольшой этажности, при прокладке сетей коммуникаций.
Инженерно-геодезические (опорные геодезические разбивочные сети) сети обладают следующими особенностями:
∙создаются на конкретных объектах;
∙имеют ограниченные размеры с небольшим числом фигур и короткими длинами;
∙плотность пунктов и точность построения сети рассчитывается от конкретных задач;
∙сеть строится, как правило, в виде свободных построений в
условной прямоугольной системе координат с привязкой к государственной сети.
1.1.3.2. Линейно-угловые сети
При установке элементов конструкций инженерных сооружений и высокоточной установке технологического оборудования создаются специальные высокоточные сети по форме, повторяющей геометрическую форму сооружения в плане. При строительстве сравнительно простых по геометрической форме
промышленных и гражданских инженерных сооружений такие сети строят в виде четырехугольников, геодезических четырехугольников или квадратов, рядов из ромбов, центральных систем. Измерение их ведут методом триангуляции, трилатерации или линейно-угловым.
Для расчета точности угловых и линейных измерений в указанных сетях применяются формулы, разработанные А. И. Дурневым, К. Р. Проворовым, К. А. Лапингом, Т. Т. Чмчяном и др.
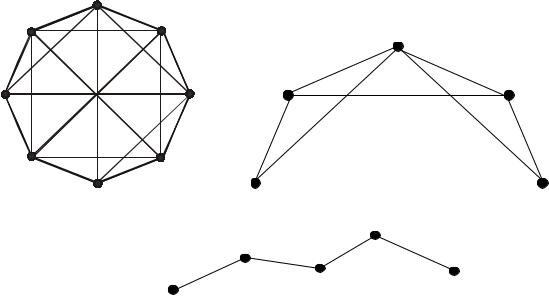
При высокоточной установке технологического оборудования развивают специальные высокоточные сети микротрилатерации: радиально-кольцевые, кольцевые и линейные (рис. 32).
а) радиально-кольцевые б) кольцевые
в) линейные
Рисунок 32 – Виды линейно-угловых сетей Методика построения таких сетей обосновывается разработкой ППГР.
В линейных и кольцевых сетях микротрилатерации взаимное поперечное положение смежных пунктов определяют с высокой точностью. С увеличением числа треугольников точность определения пунктов понижается. Для повышения
точности взаимного поперечного положения удаленных пунктов дополнительно измеряют углы, создавая линейно-угловые сети. Применение различных схем
кольцевых и линейных сетей микротрилатерации зависит от точности разбивки сооружений.
1.1.3.3. Геодезические засечки
Этот метод весьма эффективен в условиях открытой, но довольно пересеченной местности. По известным дирекционному углу α1 (рис.33), длине первой стороны S1, измеренным при ней углам A1, B1 и A1′,B1′ определяют прямой угловой засечкой боковые пункты M и M' и дирекционные углы на них. Измерением в точке II дополнительно углов A2, A3 и A2' ,A3', находят дирекционный угол линии IIIII и направления на боковые точки N, N'. По
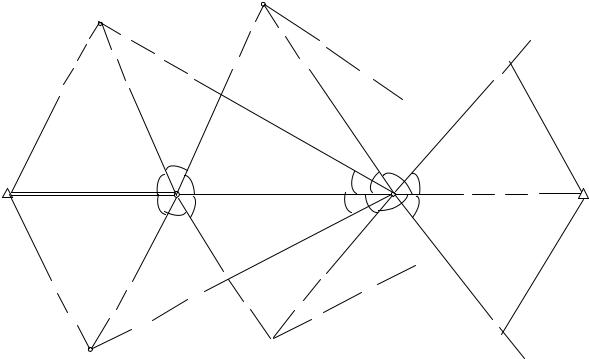
измеренным в точке III углам B2 и B2' дважды получают значение линии II -III,
которая становится исходной для дальнейших аналитических построений и вычислений.
N
M
|
|
|
ΙΙ |
|
III |
|
|
|
|
A2 |
B3 |
A4 |
|
|
S1 |
B1 |
A3 |
B2 |
A5 |
E |
A |
α1 |
B1’ |
A3' |
B2' |
A5' |
|
|
|
|
A2' |
B3' |
A4' |
|
 N’
N’
M’
Рисунок 33 – Схема определения координат способом засечек
|
|
|
S1 |
|
= |
MII |
|
|
||
sin(180 − (A − B )) |
sin A |
|
|
|||||||
|
|
|
1 |
1 |
|
|
1 |
|
||
MII |
|
= |
|
|
II − III |
|
|
|
||
sin B |
2 |
|
sin(180 − (A + B |
2 |
)) |
|||||
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|||
Длину стороны с порядковым номером i ходовой линии в сети из двух фигурных засечек вычисляют по теореме синусов дважды:
|
= S1 × |
sin A sin( A |
|
+ B |
2 |
)sin A ....sin( A i −2 |
+ B i−2 |
) |
= |
||||||||||||||
Si |
|
|
1 |
2 |
|
|
|
|
|
|
3 |
|
|
2 |
|
2 |
|
||||||
|
sin( A |
+ B )sin B |
2 |
sin( A |
+ B |
3 |
).....sin B i−2 |
|
|||||||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
||||
|
× |
sin A |
sin( A |
+ B |
2 |
)sin A ....sin( A i−2 |
+ B |
i−2 |
) |
|
|
|
|||||||||||
S1 |
|
1 |
|
2 |
|
|
|
|
|
|
|
3 |
|
2 |
|
2 |
|
|
|
|
|||
sin( A |
+ B |
)sin B |
2 |
sin( A |
+ B |
).....sin B |
i−2 |
|
|
|
|
||||||||||||
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
3 |
3 |
|
|
2 |
|
|
|
|
||
