геодезия конспект лекций
.pdf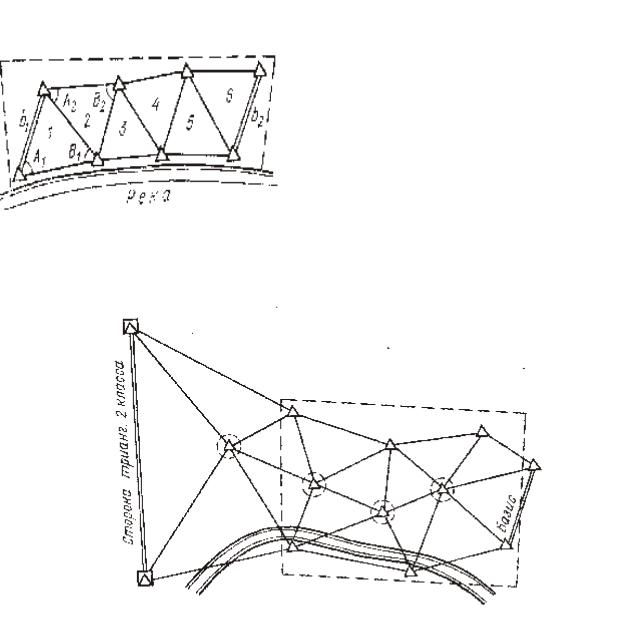
отдельных пунктов в процессе строительства и сгущения планового обоснования
исполнительных съемок. |
|
|
|
Триангуляция строится из |
одной |
фигуры или сочетания нескольких |
|
фигур (геодезические |
четырехугольники, |
центральные системы), в зависимости |
|
от местных условий, |
размеров |
и конфигурации площадки (рис. 43). |
|
|
|
а) Ряд триангуляции |
|
б) Сдвоенные ряды триангуляции
Рисунок 43- Схема развития сетей триангуляции
В сети триангуляции намечают не менее двух базисов, в качестве которых обычно измеряют непосредственно стороны сети. При этом, пункты,
закрепляющие базисные |
стороны, стремятся |
строго совмещать со сторонами |
||||
сетки. |
В этом случае, |
при измерении |
базиса, в качестве створных точек |
|||
определяют положение расположенных на нем пунктов сетки. |
||||||
В |
зависимости от |
принятой |
при |
проектировании системы координат |
||
одному из пунктов триангуляции присваиваются |
начальные координаты, а одной |
|||||
из ее сторон -начальный дирекционный угол. |
|
|
||||
|
При |
обработке |
триангуляции |
базисы вычисляют на плоскости |
||
(поправки за |
приведение |
к проекции |
Гаусса и |
уровню референц -эллипсоида не |
||
вводят). |
|
|
|
|
|
|
Расчет точности измерений в триангуляции выполняют по проекту сети,
составленному с использованием полученного при изысканиях картографического
материала. |
|
Полигонометрия 1- го |
порядка представляет собой систему вытянутых |
ходов (для сеток из квадратов или одинаковых прямоугольников, стороны ходов равны между собой). Отличительной чертой таких ходов являются короткие стороны (в среднем около 200 м), что приводит к большому числу сторон в ходе, а следовательно, требует повышения точности угловых измерений. Поэтому, если полигонометрия представляет систему полигонов, рекомендуется осуществить передачу дирекционных углов на узловые точки. Здесь также может быть использован способ измерения в комбинациях.
Полигонометрию 1-го порядка прокладывают |
между |
пунктами |
триангуляции или строят в виде самостоятельных систем. |
|
|
Исходя из средней ошибки положения пункта полигонометрии 1-го порядка |
||
±2,7 см, получим среднюю ошибку в конце хода ±5,4 см |
и предельную ±10 см. |
|
При длине хода между пунктами триангуляции 2-3 км - это составит 1:20 000 - 1:30
000, что |
соответствует |
полигонометрии 4-го |
класса. Однако измерения |
(особенно |
угловые) |
следует выполнять с |
особой тщательностью, так как |
наименьшая длина стороны в полигонометрии 4-го класса - 250 м, а в строительной сетке, как правило, все стороны в среднем равны 200 м.
Поскольку стороны каркаса служат базисами для тригонометрических сетей 2-го порядка, точность в измерениях должна быть в 1,5-2 раза выше точности определения сторон этих сетей.
Сети второго порядка требуют большого объема полевых работ, часто в весьма неблагоприятных условиях. Строиться они могут в виде ходов
полигонометрии между пунктами каркаса или заменяющих их тригонометрических построений (микротриангуляции, геодезических засечек, четырехугольников без диагоналей).
Специфическая форма этих сетей, обусловленная построением их по заранее установленным временным пунктам, приводит, к образованию вытянутых ходов с равными сторонами, цепочек, равнобедренных прямоугольных треугольников и т. п. В последние годы широкое применение для построения сетей 2-го порядка
получили микротриангуляция, |
метод геодезических засечек и четырехугольников |
|||||
без диагоналей. |
|
|
|
|
|
|
В случае, |
когда местные условия |
препятствуют |
постановке угловых |
|||
измерений, |
но |
позволяют |
организовать |
линейные |
с |
использованием |
светодальномеров, для построения сетей 2-го порядка можно использовать микротрилатерацию или линейные геодезические засечки.
Переход от более простой полигонометрии к сетям микротриангуляции, геодезических засечек, четырехугольников без диагоналей, микротрилатерации и линейных геодезических засечек объясняется тем, что для строительных сеток
особо важно надлежащим образом выдержать точность во взаимном расположении пунктов по направлениям осей строительной системы координат. С этой точки зрения система из параллельных ходов полигонометрии 2-го порядка не является лучшей, ибо в середине хода могут быть значительные взаимные сдвиги. Цепочки микротриангуляции и микротрилатерации связывают воедино по два ряда, а цепочки угловых и линейных геодезических засечек - по три ряда пунктов сетки. Иногда их удается запроектировать таким образом, что
технологически связанные группы сооружений располагаются в пределах цепочки.
Наиболее рациональной с точки зрения построения сетки является сеть четырехугольников без диагоналей, повторяющая конфигурацию сетки и
создающая взаимную связь между пунктами по всем направлениям вдоль осей строительной системы координат. Однако, с точки зрения сохранности пунктов,
этот способ может привести к увеличению разрыва между постановкой временных и постоянных знаков, ибо для вычисления элементов редукции нужно построить и уравнять всю сеть целиком. Кроме того, иногда может оказаться целесообразным, по мере проведения вертикальной планировки, строить сети 2-го порядка, чтобы быстрее начинать разбивочные работы. Цепочки позволяют решать вопрос оперативнее, чем сплошные сети. Анализ отечественного опыта показывает, что для создания сетей 2-го порядка особо эффективны метод четырехугольников без диагоналей и метод геодезических засечек.
1.1.4.5.Оценка точности построения строительной сетки
При расчете точности строительной сетки следует исходить из того, что она должна, во-первых, обеспечить разбивку основных осей сооружения; во-вторых - служить основой для исполнительной съемки. В связи с этим, предъявляются следующие требования к точности построения строительной сетки:
1.) чтобы обеспечить разбивку основных осей - ошибки во взаимном положении соседних пунктов в заполняющей сети не должны превышать 1:10 000;
если сторона принята равной S=200 м, то ошибка должна быть < 20 мм;
2.) если строительная сетка используется в качестве основы для исполнительной съемки, то важно выдержать необходимую точность общего расположения пунктов; предельные ошибки положения пунктов строительной сетки относительно исходных не должны превышать 0,2 мм в масштабе плана ( при М 1:500 t=10 см).
Произведем расчет точности построения строительной сетки.
Если сторона сетки S=200 м, при двух стадийном построении сетки, для ошибки взаимного планового положения двух смежных пунктов будем иметь:
Мвз= 20 мм,
Мвз= 
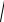mI 2 + mII 2 .
Примем коэффициент понижения точности 2, тогда:
|
m |
|
|
|
m |
2 |
|
|
|
|
|
|
|
|
|
|
|
= m 125, = 20мм ; |
|||||
m = |
II |
Þ М |
вз |
= |
( |
II |
|
)2 + m 2 |
|||
|
|
|
|||||||||
I |
2 |
|
|
2 |
|
II |
II |
||||
|
|
|
|
|
|
|
|
|
|||
20
mII = 
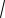125, » ±18мм;
mI = mII = ±19мм. 2
Допустимая СКО взаимного положения пунктов в заполняющей сети ±18 мм,
а в каркасной - ±9 мм. Тогда:
mI = mSI |
2 + ( |
mαI |
)2 S2 £ 9мм ; |
|
r |
||||
|
|
|
mII = 
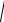mSII 2 +( mrαII )2 ´ S2 £ 18мм ,
где mSI, mSII - СКО определения длин сторон сетей I и II порядка;
mαI, mαII - СКО определения дирекционного угла в сетях I и II порядков. mS2+ mα 2= m2, пусть mS= mα= m2, тогда:
m = |
m |
|
, m = |
m ´ |
r |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
||||||||||||||
|
S |
2 |
|
|
α |
S 2 |
|||||||||||
|
|
|
|
|
|
||||||||||||
Отсюда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
= |
9 |
|
|
|
= 6,4мм » 5мм |
||||||||||
|
|
|
|
|
|
|
|
||||||||||
SI |
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
m |
|
|
= |
18 |
|
|
|
= 12,8мм » 10мм |
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||
SII |
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
mαI = 200000206265´´ 92 » 6 ²»5²
m |
= |
206265 ´18 |
» 13,2 ²» 10² |
||
|
|
||||
200000 ´ 2 |
|||||
αII |
|
|
|||
Это допустимые СКО для сетки, которая будет использована для выноса осей зданий.
Для сетки, которая будет использована для исполнительной съемки:
mI2+mII2=5 см2,
принимаем коэффициент понижения точности k=1,5, тогда:
mI = mII Þ mII = 4,1см 1,5
|
|
|
|
|
|
|
|
|
|
mI=2,7 см. |
Для расчета точности используется формула СКО в конце хода для |
||||||||||
одиночного хода светодальномерной полигонометрии: |
||||||||||
M 2 |
= m 2 |
×n× |
mβ |
2 |
+ |
n + 3 |
× L2 - для ×вытянутого× хода |
|||
r2 |
|
|||||||||
|
S |
|
|
12 |
|
|||||
|
|
|
|
|
|
2 |
×[DЦТ |
2 ]- для ×изогнутого× хода |
||
M 2 |
= mS |
2 |
×n + |
mβ |
|
|||||
2 |
|
|||||||||
|
|
|
|
|
r |
|
|
|
|
|
где n -число сторон хода;
[DЦТ2] - сумма квадратов расстояний от центра тяжести до текущих точек. Так как mI=27 мм в наиболее слабом месте (в середине хода), тогда:
M ≤ 2mI ≤ 5,2мм.
Для полигонометрии требуется выполнение этого условия, что достигается следующим путем:
∙повышают точность угловых и линейных измерений;
∙при неизменных mβ и mS общий ход по периметру разбивают на несколько ходов (полигонов);
∙увеличивают длину сторон сетки.
1.1.4.6. Контрольные измерения строительной сетки
Контрольные измерения предназначены для проверки правильности редуцирования и получения данных о качестве построенной строительной сетки.
Вначале выполняют контрольные угловые измерения, охватывающие всю сетку. Если на отдельных пунктах обнаруживаются ошибки, выходящие за пределы принятых при построении строительной сетки допусков, выполняют
повторное редуцирование или дополнительные измерения с целью обнаружения промахов. Контрольные угловые измерения выполняют на пунктах, расположенных в шахматном порядке (рис. 44), с таким расчетом, чтобы охватить все пункты сетки. Для ускорения работы рекомендуется измерять углы
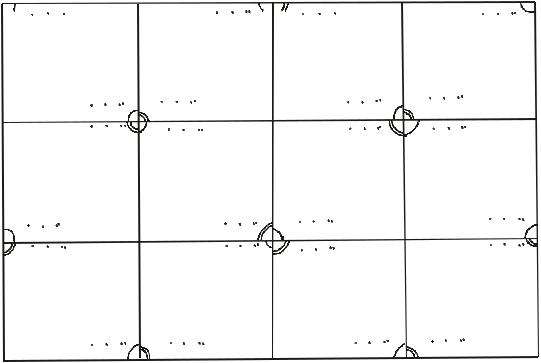
одновременно двумя теодолитами, используя общие визирные цели. По величинам отклонения значений углов от проектных судят о качестве построения сетки.
A18
89
59 43
90 00 18 
89 59 58
90 00 15 
A16 |
90 08 23 |
90 00 03 |
90 00 00 |
89 59 58 |
|
89 59 57 |
89 59 37 |
89 59 49 |
90 00 13 |
||
|
A14 |
90 00 04 |
90 00 12 |
89 39 42 |
90 00 08 |
|
89 59 48 |
90 00 02 |
90 00 04 |
90 00 08 |
||
|
A12 |
90 00 08 |
90 00 02 |
|
89 59 49 |
90 00 14 |
|
|
B16 |
B18 |
B20 |
|||||
B12 |
|
B14 |
|
Рисунок 44 - Угловые контрольные измерения в строительной сетке
Естественно, что при этом целесообразно получить данные о линейных
величинах отклонения наблюдаемых точек от |
линий, |
на которых они |
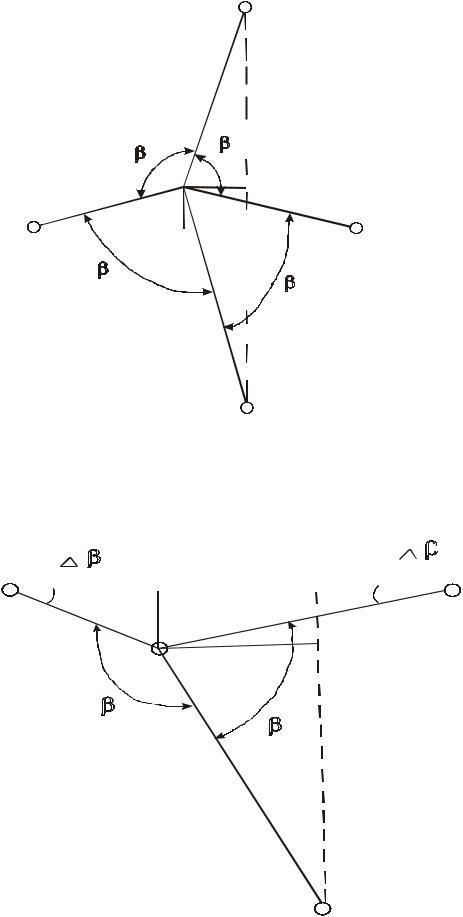
расположены. Принимая, что пункты 1, 2, 3 и |
4 (рис. |
45), между которыми |
расположен пункт 5, определены безошибочно и соединяющие их линии 1 - 3 и 2 - 4 пересекаются под прямым углом, можно определить линейные смещения а и в этих точек от створов по формулам:
a = |
S1 × S2 |
× d A ; |
|
b = |
S3 ×S4 |
× dB |
, |
||||||
|
|
|
|
|
|||||||||
|
S1 + S2 |
r |
|
|
|
S3 + S4 |
r |
|
|||||
которые для сетки квадратов при S1 = S2 = S3 = S4 = S |
принимают вид: |
||||||||||||
|
|
S |
|
|
|
|
|
S |
|
|
|||
|
a = |
|
×d A |
; |
b = |
|
×dB . |
|
|
||||
|
2×r |
2×r |
|
|
|||||||||
В этих формулах:
δA=180° - (β2 + β3);
δB=180° - (β3 + β4).
3
S2
A) пункт 5 внутри сетки
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
S4 |
|
|
|
|
|
A |
|
|
|
|
|
|
|
S3 |
||||||
|
5 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
S1
1
Рисунок 45 – Схема определения величин отклонений в положении пунктов
строительной сетки
Б) пункт 5 на временном контуре сетки
2
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
A |
|||||||||||||||
|
S1 |
|
|
|
|
|
|
|
|
|
|
|
S2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
5 |
|
|
|
B |
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
S3
4
Рисунок 46 - Схема определения величин отклонений в положении пунктов
строительной сетки
При расположении точки на внешнем контуре сетки (рис. 46) находят смещение a перпендикулярно к периметру, а смещение b вдоль периметра - из выражения:
db b = S3 × r ,
причем величину db находят по формулам:
db = 90°-(b1 ± Db1 )
Db(1)2 = (a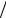
S( 1)2 )×r
В последней формуле в скобках знак "плюс" принимают при b1 + b2 <180°, а знак "минус" - b1 + b2 ³180°.
Рассмотрим пример. Для пункта A16 B14 (см. рис. 45) строительной сетки со стороной квадрата S=200 м имеем:
b1 =90° 00'23"; b2 =90° 00'03" ; b3 =89° 59'37" ; b4 =89° 59'57".
Согласно формулам, приведенным выше:
dA=180° - 179°59¢40²=20²; dB=180° - 179°59¢34²=26².
Затем определяем линейные смещения:
|
b = |
S |
×dB = 12,6мм; |
|
2 ×r |
||
Для расположенного на внешнем |
контуре сетки пункта A18 B16 имеем b1 |
||
=90° 00'19"; |
b2 =89° 59 57". По значению dA =16" находим a = 7.7 мм. Затем |
||
определяем: |
|
|
|
Db=206265×7,7 /200 000=8² ;
db=½90° - (b1 ± Db1)½= ½90° - (90°00¢19² - 8²)½= 11²; b = S3 × drβ = 10,6мм.
На особо ответственных объектах можно выполнять сплошной контроль построения сетки путем проложения азимутальных ходов. В этом случае между
проконтролированными пунктами каркаса прокладывают ходы по линиям сетки, параллельным осям абсцисс и ординат, причем измеряют в них только углы поворота, а затем вычисляют дирекционные углы. Абсциссы вычисляют по ходам,
параллельным оси ординат, ординаты - по ходам, параллельным оси абсцисс. |
|
||
При использовании светодальномеров можно измерять в |
ходах только |
||
линии, образуя продольные линейные ходы, |
вытянутые вдоль оси ординат, |
и |
|
поперечные, вытянутые вдоль оси абсцисс. Стороны поперечных |
ходов а этом |
||
случае являются приращениями абсцисс, |
а стороны продольных ходов |
- |
|
приращениями ординат. |
|
|
|
Оба способа могут быть использованы и для построения сетей 2-го порядка на небольших площадках, а также для сгущения и восстановления строительных сеток.
1.1.4.7. Перевычисление координат
Для увязки строительной сетки с соседними объектами перевычисляют ее координаты в государственную или местную систему, используя формулы:
X = a + x×v×cosq - y×v×sinq ;
Y = b + x×v×sinq + y×v×cosq ,
где X, Y - координаты пункта в государственной или местной системе; x, y - координаты того же пункта в системе строительной сетки;
a, b - координаты условного начала в государственной (или местной) системе; v - коэффициент изменения масштаба сети в связи с редуцированием на
плоскость в проекции Гаусса и приведением к поверхности эллипсоида Красовского;
q - разность дирекционных углов соответствующих направлений в государственной и строительной системах координат.
Для перевычисления достаточно знать координаты двух пунктов в той и другой системе. Однако, для контроля желательно иметь три пункта. Зная