
zadachi_с решениями
.pdf
Основымолекулярнойфизики
итермодинамики
1. Основные понятия и положения молекулярно-кинетической теории
1.1. Определить массу одной молекулы кислорода O2.
Äàíî:
M = 32æ10–3 êã/ìîëü, NA = 6,02æ1023 ìîëü–1.
Найти m0.
Решение.
M
1 - é ñ ï î ñ î á : m0 = NA , ãäå Ì – молярная масса, NA – постоянная Авогадро;
m0 |
= |
32 |
10−3 |
êã/ìîëü |
= 5,3æ10–26 êã. |
|
|
|
23 |
−1 |
|||
|
|
6,02 10 |
ìîëü |
|
||
2 - é ñ ï î ñ î á :
m0 = 32 à.å.ì. = 1,66æ10–27 êãæ32 = 5,3æ10–26 кг. Ответ: m0 = 5,3æ10–26 êã.
1.2.Выразить массу молекулы воды в килограммах, если известно, что ее относительная молекулярная мас-
са равна 18 а.е.м.
Решение: m0 = 18 à.å.ì. = 1,66æ10–27 êãæ18 =
=3æ10–26 êã.
1.3.Сколько молекул воздуха содержится в комнате объемом 60 м3 при нормальных условиях? Молярная масса воздуха M = 29æ10–3 кг/моль, плотность воздуха ρ 0 = 1,29 êã/ì3.
Äàíî:
M = 29æ10–3 êã/ìîëü, ρ 0 = 1,29 êã/ì3,
V0 = 60 ì3,
NA = 6,02æ1023 ìîëü–1.
Найти
N.
Решение.
Число молекул N = mm , ãäå
0
m — масса воздуха в комнате; m0 — масса одной молекулы.
M
Íî m = ρ 0V0; m0 = NA .
35

Находим число молекул, содержащихся в воздухе комнаты:
|
N = |
ρ 0V0NA |
; |
|
|
|
|
|
|
|
|||
|
|
|
M |
|
|
|
|
1,29 êã/ì3 60 ì3 |
6,02 1023 |
ìîëü−1 |
|||
N = |
|
|
|
= 1,6æ1027. |
||
29 10−3 |
êã/ìîëü |
|
||||
Ответ: N = 1,6æ1027.
1.4. Масса 14,92ж1025 молекул инертного газа составляет 5 кг. Какой это газ?
Äàíî: |
|
|
|
|
|
|
Решение. |
|
|
|||
|
|
|
|
|
|
|
|
|||||
N = 14,92æ1025, |
|
|
|
|
|
|
m |
M |
||||
m = 5 êã, |
|
|
|
|
|
|
|
|||||
|
|
|
Òàê êàê N = |
|
, à m0 = |
|
|
|||||
23 |
–1 |
|
|
, |
||||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
m0 |
NA |
||||
NA = 6,02æ10 ìîëü . |
|
|
|
|
|
|
|
|
|
|||
Найти |
|
|
òî |
N = |
mNA |
. Отсюда |
|
|
||||
M. |
|
|
|
M |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
M = |
|
mNA |
; |
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
M = |
5 êã |
6,02 1023 ìîëü |
− 1 |
|
|
|
|
|
|
|||
|
14,92 |
25 |
|
|
= 20,17æ10–3 êã/ìîëü. |
|||||||
|
|
10 |
|
|
|
|
|
|
|
|
||
Ответ: M = 20,17æ10–3 êã/ìîëü.
1.5. Определить среднюю длину свободного пробега молекул гелия при нормальных условиях, если молекулы, двигаясь со средней скоростью 1380 м/с, испытывают 6,9ж109 столкновений в секунду.
Äàíî: |
|
|
|
|
|
|
|
Решение. |
||||||||||||
|
|
|
= 1380 ì/ñ, |
|
|
Средняя длина свободного пробе- |
||||||||||||||
v |
|
|
||||||||||||||||||
|
|
|
= 6,9æ109 ñ–1. |
|
га молекул |
|
|
|
|
|
|
|
|
|||||||
z |
|
|
|
|
|
|
|
|
|
|||||||||||
Найти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|||||||
|
|
|
|
|
|
λ = |
|
|
|
; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
λ . |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|||||||
|
1380 ì / ñ |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
= 2æ10–7 |
ì = 2æ10–4 ìì. |
|||||||||||
|
|
|
|
λ |
= |
|||||||||||||||
|
|
|
|
6,9 10 |
9 |
ñ |
− 1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: λ = 2ж10–4 ìì.
36

1.6. Молекулы аргона при нормальных условиях испытывают 6ж109 столкновений в секунду при средней длине свободного пробега 6,35ж10–8 м. Определить среднюю скорость поступательного движения молекул аргона.
Äàíî: |
|
|
Решение. |
|||||||||||
|
|
|
|
= 6æ109 ñ–1, |
Из формулы средней длины сво- |
|||||||||
z |
||||||||||||||
|
|
|
= 6,35æ10–8 ì. |
бодного пробега находим |
||||||||||
|
λ |
|||||||||||||
Найти |
|
|
|
|
|
|
|
|
|
|||||
|
|
= λ |
|
; |
||||||||||
|
|
|
|
|
|
|
|
v |
z |
|||||
v . |
||||||||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
= 6,35æ10–8 ìæ6æ109 ñ–1 = 381 ì/ñ. |
||||||||
|
|
|
|
v |
||||||||||
Ответ: v = 381 ì/ñ.
1.7. Определить концентрацию молекул кислорода, если они при средней скорости 400 м/с испытывают в среднем 8ж109 столкновений в секунду. Эффективный диаметр молекулы кислорода 3ж10–10 ì.
Äàíî: |
|
Решение. |
|
||||||||
|
|
|
|
|
= 400 ì/ñ, |
Концентрация молекул газа |
|||||
v |
|||||||||||
|
|
|
= 8æ109 ñ–1, |
|
|
|
|
|
|
||
z |
|
|
z |
|
|
||||||
dýô = 3æ10–10 ì. |
|
n = |
; |
|
|||||||
|
|
|
|
|
|
|
2 |
π |
d2 |
v |
|
|
|
|
|
|
|
|
|||||
Найти |
|
|
|
ýô |
|
|
|||||
|
|
|
|
|
|
||||||
n. |
|
n = |
8 109 |
ñ− 1 |
|||||||
|
|||||||||||
|
|
|
|
|
|
|
|
= |
|||
|
|
|
|
|
|
1,41 3,14 9 10− 20 |
ì2 400 ì / ñ |
||||
= 5æ1025 ì–3.
Ответ: n = 5æ1025 ì–3.
2. Основное уравнение молекулярнокинетической теории идеального газа
2.1. Определить среднюю кинетическую энергию поступательного движения одной молекулы воздуха при нормальных условиях. Концентрация молекул воздуха при нормальных условиях n0 = 2,7æ1025 ì–3.
37

Äàíî: |
|
|
|
|
|
Решение. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
T0 = 273 K, |
|
|
|
Из основного уравнения молеку- |
|||||||||||||
p0 = 105 Ïà, |
|
лярно-кинетической теории газов |
|||||||||||||||
n = 2,7æ1025 |
ì–3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 p0 |
|
||
Найти |
|
|
p0 = |
|
n0 |
Eê выразим: Eê = |
; |
||||||||||
|
3 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n0 |
|||
|
Eê . |
|
|
|
|
|
|
3 105 Í / ì2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Eê = |
|
= 5,6æ10–21 Äæ. |
||||||||||
|
|
|
|
2 2,7 1025 ì− 3 |
|||||||||||||
Ответ: Eê = 5,6æ10–21 Äæ.
2.2. На сколько кельвин понизилась температура 10 моль идеального газа при постоянном объеме, если его внутренняя энергия уменьшилась на 623 Дж? Молярная теплоемкость Cm = 12,46 Дж/(мольжK).
Äàíî: |
|
|
Решение. |
||||
ν = 10 ìîëü, |
|
Òàê êàê œU = Cmν œT, òî |
|||||
Cm = 12,46 Дж/(мольжK), |
|
|
|
||||
œU = 623 Äæ. |
|
œT = |
∆ |
U |
|||
|
|
|
|
|
; |
||
|
|
C |
ν |
||||
Найти |
|
|
|||||
|
|
|
|
m |
|||
œT. |
|
|
|
|
|
|
|
623 Äæ |
|
|
|
|
|||
œT = |
|
= 5 K. |
|||||
12,46 Äæ/ (ìîëü Ê) 10 ìîëü |
|||||||
Ответ: œT = 5 K. |
|
|
|
|
|
|
|
2.3. Определить среднюю квадратичную скорость молекул азота при нормальных условиях, т. е. при p0 = = 105 Па и плотности ρ 0 = 1,25 êã/ì3.
Äàíî: |
|
|
|
|
|
|
|
|
|
Решение. |
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
p |
= 105 Ïà, |
|
|
В основном уравнении молеку- |
||||||||||||||
ρ |
00 =1,25 êã/ì3. |
|
лярно-кинетической теории газов |
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
= ρ 0 è |
||
Найти |
|
|
|
2 |
|
|
|
|
||||||||||
|
|
|
p0 = |
|
m0n0v |
заменим m0n0 |
||||||||||||
|
|
|
êâ. |
|
|
|
3 |
|
||||||||||
|
v |
|
|
|
выразим |
|
êâ: |
|
êâ = |
3p0 |
; |
|
||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
v |
v |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ 0 |
|
|
|
|
|
|
|
êâ = |
3 105 Í / ì2 |
|
= 490 ì/ñ. |
|
|||||||||
|
|
|
|
v |
3 |
|
|
|||||||||||
|
|
|
|
|
|
|
1,25 êã / ì |
|
|
|
|
|
|
|
||||
Ответ: vêâ = 490 ì/ñ.
38
2.4. Определить изменение внутренней энергии 5 моль одноатомного идеального газа при повышении его температуры на 50 K и при неизменном объеме. Молярная теплоемкость Cm = 12,46 Дж/(мольжK).
Äàíî: |
Решение. |
|
ν = 5 ìîëü, |
Изменение внутрен- |
|
Cm = 12,46 Дж/(мольжK), |
|
ней энергии идеального |
V = const, |
ãàçà |
|
œT = 50 K. |
|
|
|
|
œU = Cmν œT; |
Найти |
|
|
œU. |
|
|
|
|
|
œU = 12,46 Дж/(мольжK)ж5 мольж50 K = 3115 Дж.
Ответ: œU = 3115 Äæ.
2.5. Определить внутреннюю энергию всех молекул воздуха в аудитории, объем которой 168 м3, при нормальных условиях.
Äàíî: |
|
Решение. |
|||
p = 105 |
Ïà, |
|
Внутренняя энергия молекул газа |
||
0 |
|
|
|
|
|
V0 = 168 ì3. |
|
U = |
3 |
p0V0; |
|
Найти |
|
|
|||
|
|
||||
U. |
|
2 |
|||
|
|
U = 1,5æ105 Í/ì2æ168 ì3 = |
|||
|
|
|
|||
|
|
= 25,2æ106 Äæ = 25,2 ÌÄæ. |
|||
Ответ: U = 25,2 ÌÄæ.
3. Уравнение состояния идеального газа. Изопроцессы и их графики
3.1. Определить температуру идеального газа, если средняя кинетическая энергия поступательного движения его молекул равна 7,87ж10–21 Äæ.
39
Äàíî:
Eê = 7,87æ10–21 Äæ, k = 1,38æ10–23 Äæ/Ê.
Найти
T.
Решение.
Òàê êàê Eê = 32 kT, ãäå
k — постоянная Больцмана, то отсюда находим
|
|
|
|
|
|
2 7,87 10− 21 Äæ |
|
|
T = |
2Eê |
; |
T = |
= 380 K. |
||||
3 1,38 10− 23 Äæ / K |
||||||||
3k |
||||||||
Ответ: T = 380 K.
3.2. Под каким давлением находится кислород в баллоне, если при температуре 27 °C его плотность 6,24 кг/м3?
Äàíî: |
|
|
|
|
Решение. |
|
|||||||
|
|
|
|
|
|||||||||
M = 32æ10–3 êã/ìîëü, |
|
|
Преобразуем |
уравнение |
|||||||||
T = 300 K, |
|
|
Клапейрона – Менделеева к |
||||||||||
ρ = 6,24 êã/ì3, |
|
|
âèäó |
|
|
|
|
|
|||||
R = 8,31 Дж/(мольжK). |
|
|
|
|
p = |
m |
RT, |
||||||
Найти |
|
|
|
|
|
|
|||||||
VM |
|||||||||||||
p. |
|
|
íî |
m |
= ρ ; следовательно, |
||||||||
|
|||||||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
V |
|
|
||||
6,24êã / ì3 |
8,31 Äæ / (ìîëü K) 300 K |
||||||||||||
p = |
ρ RT |
; p = |
|
|
|
|
|
= |
|||||
|
|
|
32 10-3 êã / ìîëü |
|
|||||||||
M |
|||||||||||||
= 4,86æ105 Í/ì2 = 4,9æ105 Ïà.
Ответ: p = 4,9æ105 Ïà.
3.3. При какой температуре средняя квадратичная скорость молекул углекислого газа CO2 равна 400 м/с?
Äàíî: |
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
= 400 ì/ñ, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M = 44æ10–3 êã/ìîëü, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 0v2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
R = 8,31 Дж/(мольжK). |
|
|
|
Òàê |
êàê Eê = |
|
è |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
Найти |
|
|
|
= |
3 kT, òî m |
|
|
2 = 3kT. Íî |
||||||||||||||
E |
|
|
||||||||||||||||||||
T. |
v |
|||||||||||||||||||||
ê |
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
m0 |
= |
|
|
, тогда |
|
Mv |
= 3kT, |
||||||||||||
|
|
|
|
NA |
|
|
|
NA |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
40
|
|
|
2 |
|
|
|
|
2 |
|
|||
|
Mv |
|||||||||||
откуда T = |
|
= |
Mv |
, ãäå kNA = R. Находим |
||||||||
3kNA |
||||||||||||
|
|
|
3R |
|
||||||||
T = |
44 10− 3 |
êã / ìîëü 16 104 ì2 / ñ2 |
= 282,4 K. |
|||||||||
|
3 |
|
8,31 Äæ(ìîëü K) |
|||||||||
|
|
|
|
|||||||||
Ответ: T = 282,4 K.
3.4. Какой объем занимает 1 кг кислорода при температуре 273 K и давлении 8ж105 Па? Молярная масса кислорода M = 32æ10–3 êã/ìîëü.
Äàíî: |
|
|
|
|
|
|
Решение. |
|
||
m = 1 êã, |
|
|
|
|
|
Из уравнения Клапейрона |
||||
T1 = 273 K, |
|
|
– Менделеева выразим V1: |
|||||||
p = 8æ105 |
Ïà, |
|
|
|
|
|
|
mRT1 |
|
|
1 |
|
|
|
|
|
|
|
|
||
M = 32æ10–3 êã/ìîëü, |
|
|
|
V = |
||||||
|
|
|
p1M |
|||||||
R = 8,31 Дж/(мольжK). |
|
|
1 |
|
||||||
|
|
|
|
|||||||
|
|
Вычисляя, находим |
||||||||
|
|
|
|
|
|
|
||||
Найти |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
V1. |
|
|
|
|
|
|
|
|
|
|
V1 = |
1 êã 8,31 Äæ / (ìîëü Ê) 273 K |
= 0,087 ì3. |
||||||||
8 |
5 |
2 |
10 |
− 3 |
êã / ìîëü |
|||||
|
10 |
Í / ì 32 |
|
|
|
|
||||
Ответ: V1 = 0,087 ì3.
3.5. При изохорном нагревании идеального газа, взятого при температуре 320 K, его давление увеличилось от 1,4ж105 äî 2,1æ105 Па. Как изменилась температура газа?
Äàíî: |
|
|
|
|
Решение. |
|||
T1 = 320 K, |
|
Так как процесс изохорный, то |
||||||
p = 1,4æ105 |
Ïà, |
|
|
|
|
|
||
1 |
5 |
Ïà, |
|
p1 : p2 = T1 : (T1 + œT); |
||||
|
|
|||||||
p2 = 2,1æ10 |
отсюда |
|
|
|
||||
T2 = T1 + œT. |
|
|
|
|||||
Найти |
|
|
|
|
œT = |
T1 p2 |
– T1; |
|
œT. |
|
|
|
|
p1 |
|||
320 K 2.1 105 |
Ïà |
|
|
|||||
œT = |
– 320 K = 160 K. |
|||||||
|
1,4 105 Ïà |
|
||||||
Ответ: œT = 160 K.
41
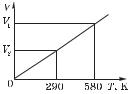
3.6. Определить начальную и конечную температуры идеального газа, если при изобарном охлаждении на 290 K его объем уменьшился вдвое. Начертить график изопроцесса в координатных осях T, V.
Äàíî: |
|
|
|
|
Решение. |
|
||
p = const, |
|
Так как процесс изобарный, то |
||||||
V2 = 0,5V1, |
V1 |
: V2 = T1 |
: T2 èëè |
|
|
|||
T2 = T1 – 290. |
|
|
||||||
|
|
V1 |
|
T1 |
|
T1 |
|
|
Найти: |
|
|
|
|||||
|
|
0,5V1 |
= |
T1 − 290 ; T1 − 290 = 2; |
||||
T1; T2. |
|
|
||||||
|
|
|
T1 |
= 580 K; T2 |
= 290 K. |
|||
На рис. 6 изображен график изобарного процесса в координатных осях T, V.
Ðèñ. 6
Ответ: T1 = 580 K; T2 = 290 K.
3.7. При изохорном охлаждении идеального газа, взятого при температуре 480 K, его давление уменьшилось в 1,5 раза. Какой стала конечная температура газа?
Äàíî: |
|
|
Решение. |
|
|
|
||||
|
|
|
|
|
||||||
T1 = 480 K, |
Так как процесс изохор- |
|||||||||
p2 = |
p1 |
èëè p1 = 1,5p2. |
íûé, òî |
|
|
|
|
|
|
|
|
|
|
|
|||||||
1,5 |
|
p1 : p2 = T1 : T2; |
|
|
||||||
Найти |
|
|
|
T1p2 |
|
T1p2 |
|
T1 |
|
|
T2. |
T2 = |
|
= |
= |
; |
|||||
|
|
|
1,5 |
|||||||
|
|
|
|
|
p1 |
1,5 p2 |
|
|||
T = 480 K : 1,5 = 320 K.
Ответ: T2 = 320 K.
42
4. Первое начало термодинамики
èприменение его к изопроцессам
4.1.Как изменится внутренняя энергия 240 г кислорода O2 при охлаждении его на 100 K?
Äàíî:
m = 0,24 êã, œT = 100 K,
M = 32æ10–3 êã/ìîëü, R = 8,31 Дж/(мольжK).
Найти:
œU.
Решение.
Изменение внутренней энергии газа массой m при его охлаждении на œT равно
œU = 52 Mm RœT;
5 |
0,24 êã 8,31Äæ/ (ìîëü K) 100 K |
|
œU = |
2 32 10− 3 êã / ìîëü |
= 15,58 êÄæ. |
Ответ: Уменьшится на 15,58 кДж.
4.2. Один килограмм углекислого газа CO2 изобарно нагрет от 268 до 400 K. Определить работу, совершенную над газом при увеличении его объема, и изменение внутренней энергии этого газа.
Äàíî:
m = 1 êã, T1 = 268 K, T2 = 400 K,
M = 44æ10–3 êã/ìîëü, R = 8,31 Дж/(мольжK).
Найти
A; œU.
Решение.
Так как процесс изобар-
íûé, òî A = pœU = Mm RœT. Изменение внутренней
энергии газа
œU = 3 Mm RœT = 3A;
A = |
1 êã 8,31 Äæ / (ìîëü K) 132 K |
= 24,93 êÄæ; |
44 10− 3 êã / ìîëü |
œU = 3A = 74,79 êÄæ.
Ответ: A = 24,93 êÄæ; œU = 74,79 êÄæ.
43
4.3. Определить начальную температуру 0,56 кг азота N2, если при изобарном нагревании до 370 K совершена работа 16,62 кДж на увеличение его объема.
Äàíî: |
|
|
|
|
|
Решение. |
|
|
|||||
|
|
|
|
|
|
|
|||||||
m = 0,56 êã, |
|
|
|
Работа газа при изобарном |
|||||||||
T2 = 370 K, |
3 |
Äæ, |
|
процессе |
A = |
|
m |
RœT, отсюда |
|||||
|
|
|
M |
||||||||||
A = 16,62æ10 |
|
|
|
|
|
|
|
|
|
|
|||
M = 28æ10–3 êã/ìîëü, |
|
œT = |
AM |
. Следовательно, |
|
||||||||
R = 8,31 Дж/(мольжK). |
|
||||||||||||
|
|
||||||||||||
|
|
|
|
|
mR |
|
|
|
|
|
|
|
|
Найти |
|
|
|
|
|
|
|
|
|
|
|
|
|
T1. |
|
|
|
T1 = T2 – œT; T1 |
= T2 – |
AM |
; |
||||||
|
|
|
mR |
||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T = 370 K – |
16,62 103 |
Äæ 28 10− 3 |
êã / ìîëü |
= 270 K. |
|
||||||||
|
0,56 êã |
8,31 Äæ / (ìîëü |
K) |
|
|
||||||||
1 |
|
|
|
|
|
||||||||
Ответ: T1 = 270 K.
4.4. Газ изобарно увеличился в объеме в три раза при давлении 3ж105 Па. Определить первоначальный объем газа, если на увеличение его объема потребовалось совершить работу 12,9 кДж.
Äàíî: |
|
Решение. |
|||
V2 = 3V1, |
|
Работа расширения газа |
|||
p = 3æ105 Ïà, |
при изобарном процессе |
||||
A = 12,9æ103 Äæ. |
A = pœV = p(V2 – V1) = 2pV1; |
||||
Найти |
|
отсюда находим |
|||
V1. |
|
|
V1 = |
A |
; |
|
|
||||
|
|
|
|||
|
|
2 p |
|||
V1 = |
12,9 103 |
Äæ |
= 2,15æ10–2 ì3. |
||
2 3 105 Í / ì2 |
|||||
Ответ: V1 = 2,15æ10–2 ì3.
4.5. При изохорном процессе газу сообщено 4ж1010 Дж теплоты. Рассчитать изменение внутренней энергии и работу по расширению газа.
44
