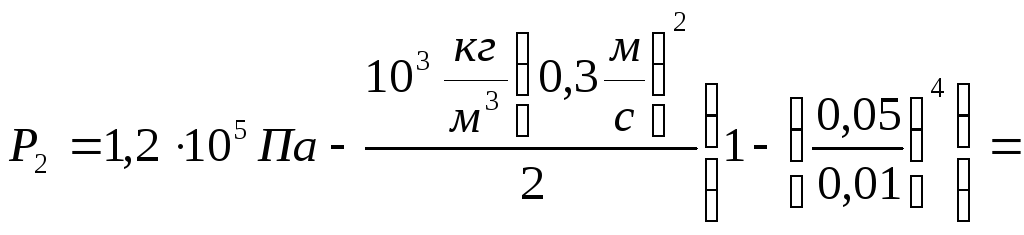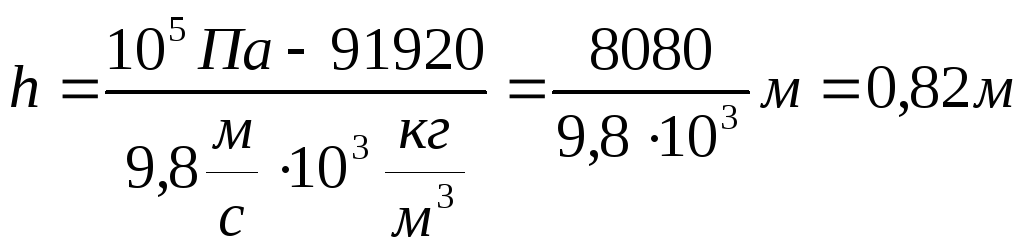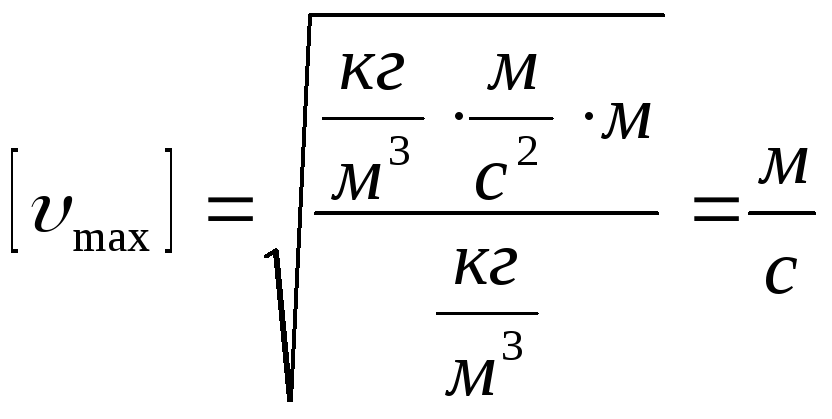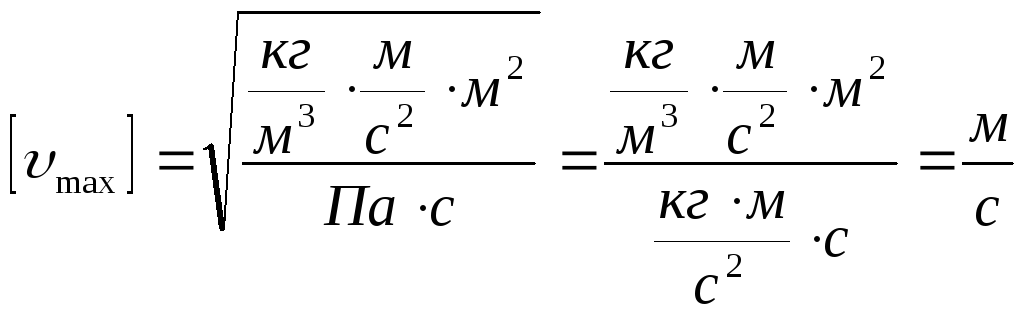- •Міністерство аграрної політики та продовольства україни
- •Критерії оцінювання знань
- •Індивідуальні домашні завдання.
- •Модуль 1.
- •Механіка.
- •Питання модульного контролю:
- •Модуль 1. Механіка і гідроаеродинаміка
- •Модуль 1 "Механіка" Мікромодуль 1м1 "Кінематика"
- •Модуль 1 "Механіка" Мікромодуль 2м1 "Динаміка" Питання для самоконтролю
- •Модуль I «Механика» Микромодуль 1м3 «Элементы гидроаэродинамики» Вопросы для самоконтроля .
- •Задачи для аудиторного и индивидуального решения Примеры решения задач
- •По уравнению Бернулли
- •Задача 2.
- •Задачи аудиторного и индивидуального решения.
- •Справочные данные Плотность ρ твердых тел и жидкостей
- •Модуль 2.
- •Молекулярна фізика та термодинаміка.
- •Питання модульного контролю
- •Модуль 2. Молекулярна фізика і термодинаміка
- •Задачі для самостійного та індивідуального розв'язання.
- •2.1. Молекулярно - кінетична теорія ідеальних газів.
- •2.2. Термодинаміка
- •Модуль 3.
- •3.1. Електростатика
- •3.2. Постійний струм
- •Довідкові таблиці
- •Магнетизм. Приклади розв’язку задач.
- •Задачі для самостійного розв'язання.
- •3.3. Магнітне поле струмів.
- •3.4. Частинка у магнітному полі
- •3.5. Ерс індукції і самоіндукції
- •Модуль 4.
- •Вычислим
- •Задачи для самостоятельного и индивидуального решения
- •4.1. Гармонические колебания
- •4.2. Электрический колебательный контур
- •4.3. Волны
- •4.4. Дифракция света
- •4.5. Тепловое излучение
- •Модуль 5.
- •Задачи для самостоятельного и индивидуального решения
- •Справочные таблицы
- •1. Масса покоя некоторых частиц, а.Е.М. Электрон - 0,00055 Нейтрон - 1,00867
- •2. Массы нейтральных атомов некоторых изотопов, а.Е.М.
Задача 2.
По горизонтальной трубке переменного сечения течет вода. Скорость воды в широком сечении υ1= 30см/с, давление Р1 = 1,2·105 Па. Диаметр узкой
части d2= 1см, широкой d1=5см
Определить:
Скорости воды υ2 и давление Р 2 в узкой части трубы.
На какую высоту h поднимется вода в вертикальной трубке, впаянной в узкую часть трубы (рис.2)? Атмосферное давление Ратм = 105 Па
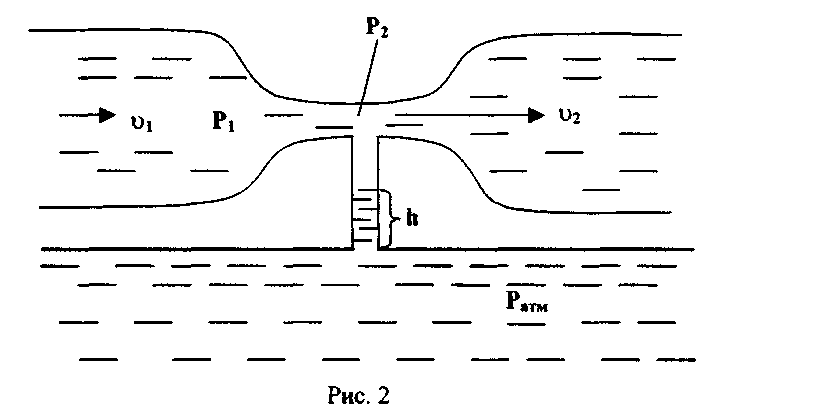
По уравнению неразрывности
![]() (1)
(1)
где S1 и S2 - площади поперечных сечений узкой и широкой частей трубы соответственно.
Отсюда
 (2)
(2)
Для горизонтальной трубки тока уравнение Бернулли принимает вид:
![]() (3)
(3)
тогда
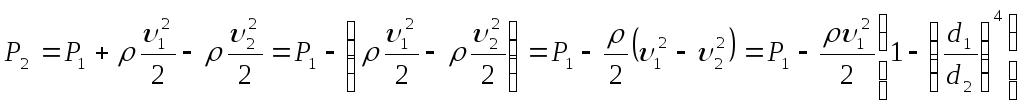
Вода поднимется в вертикальную трубку в том, случае, если атмосферное давление (под ним находится вода в нижнем сосуде) больше давления P2.
Вода в трубке установится на таком уровне, что давление столба воды
ρ будет равно Ратм-P2. Так как Р = ρqh, то
ρqh= Ратм-Р2 (4)
Отсюда
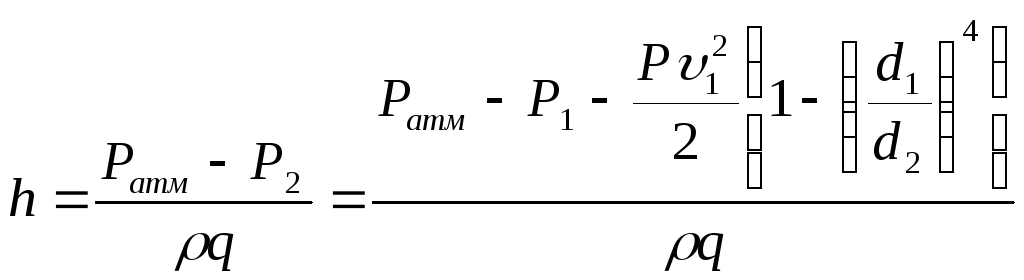
Вычисления проведем в СИ:
Дано:
|
υ1=0,3м/с P1=1,2·103 Па d2=0,01м d1=0,01м Ратм=105Па ρ =103 кг/м3
|
|
|
υ 2-? Р2-? h-? |
Высота подъема
|
Задача 3
Найти
наибольшую скорость, которую может
приобрести стальной шарик (![]() )
радиусом 3,99 мм, свободно падающий в
воздухе. (
)
радиусом 3,99 мм, свободно падающий в
воздухе. (![]() ).
Коэффициент сопротивленияСх
принят
равным 0,5.
).
Коэффициент сопротивленияСх
принят
равным 0,5.
На шарик, падающий в воздухе вертикально вниз, действуют три силы:
сила тяжести
![]() , (1)
, (1)
где r - радиус шарика;
сила Архимеда
![]() (2)
(2)
и сила сопротивления Fc, величина которой находится по формуле
![]() (3)
(3)
где ν -скорость движения тела, Сх - коэффициент сопротивления, S - площадь наибольшего сечения шарика.
F
 C При
наибольшей скорости
результирующая
сила, приложенная к шарику, равна 0,
движение его становится равномерным.
C При
наибольшей скорости
результирующая
сила, приложенная к шарику, равна 0,
движение его становится равномерным.
![]() (4)
(4)
F
 A Поскольку
A Поскольку
![]() ,
то
из сравнения формул (1) и (2) следует,
FА
<< mg, так
что равенство (4) принимает вид
,
то
из сравнения формул (1) и (2) следует,
FА
<< mg, так
что равенство (4) принимает вид
mg
Рис.
3 ![]()
Площадь сечения S = πr2 , тогда уравнение (5) запишем в виде
![]()
отсюда ![]()
Дано: Проверим размерность:
|
ρ = 7,8 г/см3=7,8·103кг/м3 ρв=1,29 кг/м3 Sx=0,5 g=9,8 м/c2 r=3,9мм=0,0039
|
Вычисление: |
|
υ max - ? |
|
Задача 4.
Алюминиевый шарик (плотность ρ = 2,7 г/см3) диаметром d = 4 мм свободно падает в сосуде, наполненным касторовым маслом (плотность ρж = 0,96 г/см3, вязкость при данной температуре составляет 0,99 Па∙с).
О
 пределить
максимальную скорость, с которой может
двигаться шарик.
пределить
максимальную скорость, с которой может
двигаться шарик.
FC На шарик, свободно падающий в жидкости, действуют три силы:
с ила
тяжести
ила
тяжести
FA ![]() (1)
(1)
m g
где
g
где
![]() - радиус;ρ
– плотность шарика;
- радиус;ρ
– плотность шарика;
Рис. 4 сила Архимеда
![]() (2)
(2)
где ρж – плотность жидкости (масла)
сила сопротивления, установленная Дж. Стоксом равна
![]() (3)
(3)
где η - вязкость жидкости;
υ - скорость шарика.
Закон Стокса справедлив для медленно двигающихся небольших тел сферической формы в безграничной жидкости (размеры сосуда много больше диаметра шарика).
Сила сопротивления с увеличением скорости возрастает, и, в конце концов, скорость шарика становится такой, что силы уравновешивают друг друга, ускорение становится равным нулю, и скорость шарика постоянной и максимальной υ= υmax
![]()
![]() (4)
(4)
Решая уравнение (4) относительно скорости υ получим
![]() (5)
(5)
Дано: Проверим размерность:
|
ρ = 2,7 г/см3=2,7·103кг/м3 ρж=0,96 г/см3=9,6·102кг/м3 η=0,99 Па·с g=9,8 м/c2 d=4мм=0,004 |
Вычисление: |
|
υ - ? |
|