11.15. Прецесія електрона

На електрон атома, що знаходиться в магнітному полі, діє момент сили

, (1)

який намагається спрямувати магнітний момент електрона у напрямкові вектора індукції магнітного поля (див.Мал.124). Застосовуючи гіромагнітне відношення , можна записати

, (2)

де момент імпульсу електрона, вектор співпадає за напрямком із вектором . За другим законом Ньютона можна записати

. (3)

Так як , то після підстановки значенняв (3) одержимо

. (3')

Лінійна швидкість обертового руху вершини деякого радіус-вектора визначається виразом

(4)

де кутова швидкість.

Порівнюючи вирази (3) та (3') з (4) видно, що величину можна прирівняти до деякої частоти з якою обертаються векторита, тобто

,

де

. (5)

Частота називаєтьсяларморівською частотою прецесії електрона навколо вектора .

Унаслідок прецесії відбувається додатковий рух електрона навколо , який створює орбітальний струм

(6)

і орбітальний магнітний момент

, (7)

де вектор ,площа проекції орбіти прецесії електрона на площинувектору. Таким чином в атомі під дією зовнішнього магнітного поля виникає додатковий магнітний момент, що направлений проти індукції зовнішнього магнітного поля.

11.16. Магнітне поле в магнетиках

11.16.1. Намагніченість середовища.

Будь - яка речовина, внесена в зовнішнє магнітне поле, намагнічується, створюючи своє власне магнітне поле. Основною характеристикою намагніченості об'єму середовища є вектор намагніченості

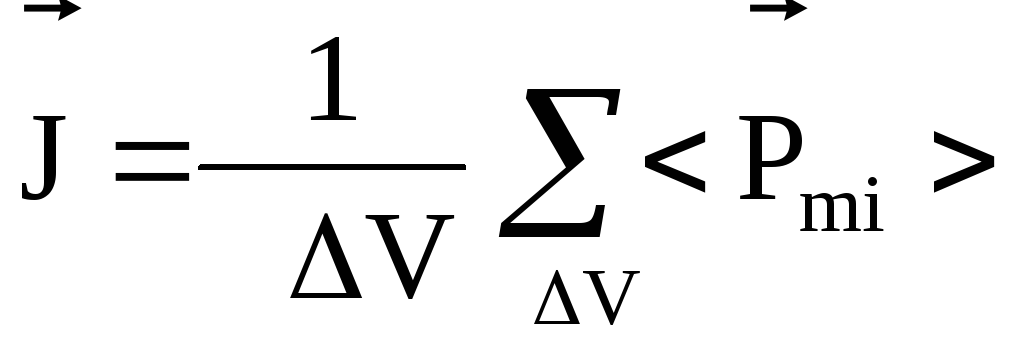, (1)

де  середнє значення магнітного моменту і-го атома. При дослідженні магнітного поля використовується така його характеристика як вектор напруженості

. (2)

Як показують досліди, для ізотропного магнетика величина вектора намагніченості середовища пропорційна напруженості магнітного поля Н, тобто

, (3)

 коефіцієнт пропорційності, який називають магнітною сприйнятливістю середовища.

11.16.2. Гіпотеза Ампера.

З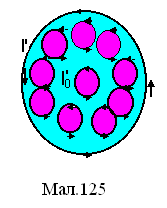а гіпотезою Ампера, виникнення магнітних властивостей у магнетиках пов'язане з молекулярними струмами , джерелом яких є рух електронів в атомах, іонах, молекулах (див.Мал.125). Ці молекулярні струми створюють поверхневий молекулярний струм І', який породжує внутрішнє магнітне поле , Векторза напрямком співпадає з вектором зовнішнього поля, а в діамагнетиках має протилежний напрямок. Реалізується це поле лише при намагніченні середовища зовнішнім полем . В підсумку поле в магнетику є сумою зовнішнього та внутрішнього магнітних полів

. (4)

11.16.3. Магнітне поле у магнетикові.

Розглянемо поле в середині магнетика у вигляді циліндра довжини L та радіуса основи r << L. Такий циліндр можна представити як довгий соленоїд з одним витком, по якому тече поверхневий струм І'. Cхему утворення І' із молекулярних струмів І₀' подано на Мал.47. В середині циліндра струми сусідніх молекул компенсують одне другого за рахунок їх протилежних напрямків, чого немає на поверхні циліндра. Густина витків циліндра n = 1/L, а величина індукції

. (5)

Магнітний момент молекулярного струму . Величина вектора намагніченості

. (6)

Підставивши І' в (5) одержимо . З іншого боку, і тоді

. (7)

Остаточно вираз для індукції у середовищі магнетика запишеться так

, (8)

де  магнітна проникливість середовища.

Частку, що приходиться на індукцію, створену молекулярними струмами, можна записати так

. (9)

По ступені й характеру намагніченості розрізняють три групи речовин: діамагнетики, парамагнетики й феромагнетики.