
- •12.Електромагнітні коливання та хвилі
- •12.1. Коливальний контур
- •12.2. Незгасаючі електромагнітні коливання
- •12.3. Вільні згасаючі електромагнітні коливання
- •12.4. Вимушені коливання
- •12.5. Змінний струм
- •12.6. Рівняння Максвелла
- •12.6.1.Теорема Остроградського-Гауса
- •12.6.2.Теорема Стокса.
- •12.6.3.Струм зміщення
- •12.6.4.Перше рівняння Максвелла.
- •12.6.5.Друге рівняння Максвелла.
- •12.6.6.Третє рівняння Максвелла.
- •12.6.7.Четверте рівняння Максвелла.
- •12.6.8.Матеріальні рівняння Максвелла.
- •12.7. Диференціальні рівняння Максвелла у діелектрику
- •12.8. Плоска електромагнітна хвиля
- •12.9.Поляризація хвилі
- •12.10. Енергія, інтенсивність та тиск електромагнітної хвилі
- •12.11. Випромінювання електричного диполя
- •12.12.Контрольні питання
12.Електромагнітні коливання та хвилі
12.1. Коливальний контур
1. Коливальним RLC-контуром (див.Мал.133) називається замкнений електричний контур, у якому є конденсатор із ємністю С, омічний опір R та соленоїд з індуктивністю L. В цей контур може бути ввімкнено джерело струму із примусовою електрорушійною силою Е= Е0cost. У загальному випадку протікання струму І в контурі на елементах контуру виникає
напруга на опорі
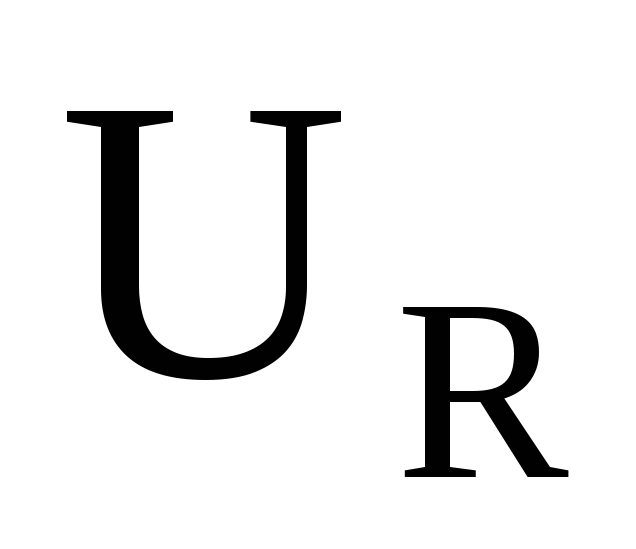 = IR,
= IR,
напруга на конденсаторі
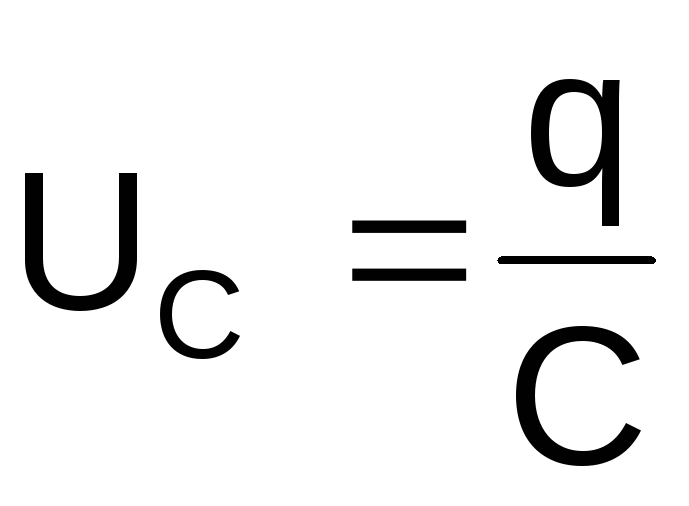 ,
,ЕРС індукції у соленоїді
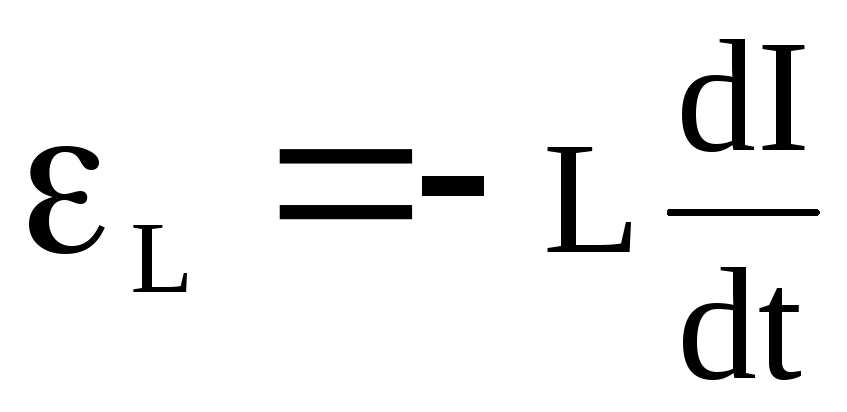 .
.
2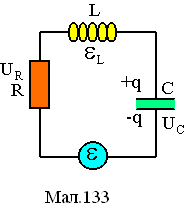 .
Застосовуючи друге правило Кірхгофа
до такого контуру, одержимо
.
Застосовуючи друге правило Кірхгофа
до такого контуру, одержимо
![]() .
(1)
.
(1)
Підставляючи відповідні вирази для напруги та електрорушійних сил, одержимо
![]() .
(2)
.
(2)
Для
одержання канонічного диференціального
рівняння коливань заряду
на обкладках конденсатора, підставимо
у (2) замість І його значення
![]() і розділимо рівняння на індуктивністьL
і розділимо рівняння на індуктивністьL
![]() ,
(3)
,
(3)
де позначено
![]() ,
,![]() ,
,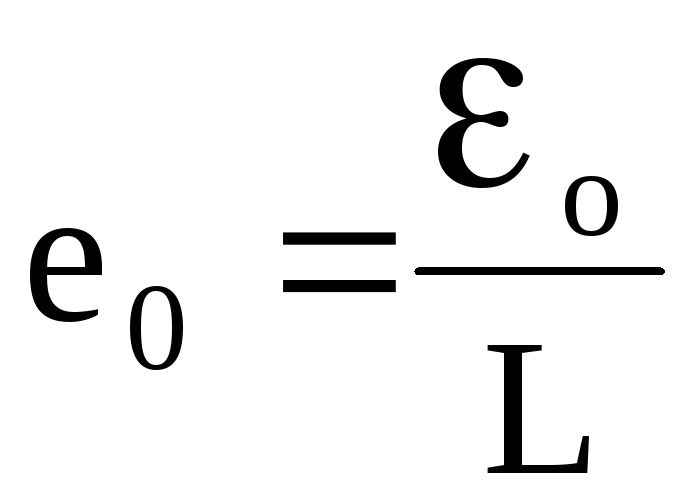 .
(4)
.
(4)
3. Диференціальне рівняння
(3) по своїй структурі тотожне з рівнянням
механічних коливань, наприклад,
коливаннями пружинного маятника. З цієї
причини ми скористаємося розв'язками
диференціального рівняння для механічних
коливань, підставляючи відповідні
значення параметрів
![]() з
(4).
з
(4).
12.2. Незгасаючі електромагнітні коливання
1. Незгасаючі вільні електромагнітні коливання, або близькі до них, виникають, коли в контурі без зовнішнього джерела енергії (Е = 0) можна знехтувати омічним опором (R 0). В цьому випадку рівняння незгасаючих електромагнітних коливань буде мати вигляд
![]() ,
(1)
,
(1)
а його розв'язком є
![]() .
(2)
.
(2)
Сталі розв'язку qo та знаходяться з початкових умов, наприклад, якщо задано величини заряду на конденсаторі та струму у контурі в деякий момент часу t.
2. Характеристики коливань
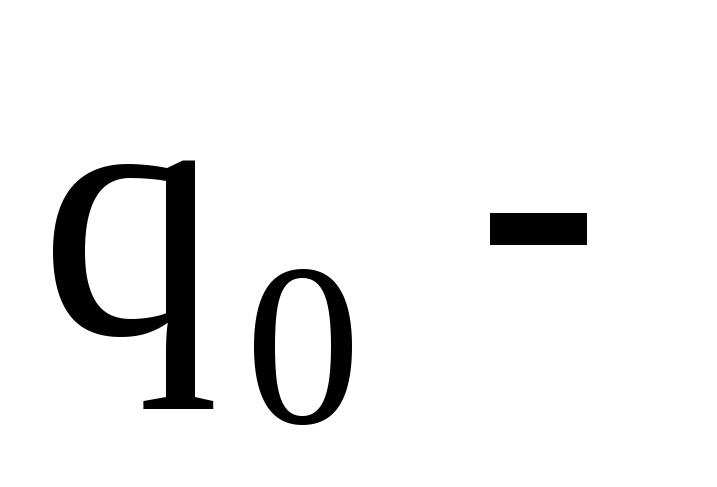 амплітуда коливань,
амплітуда коливань,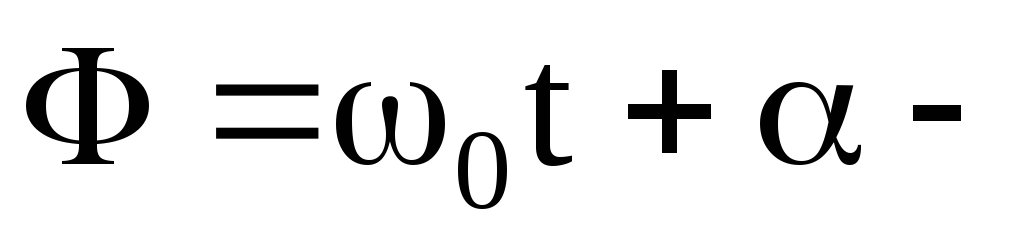 фаза коливань,
фаза коливань,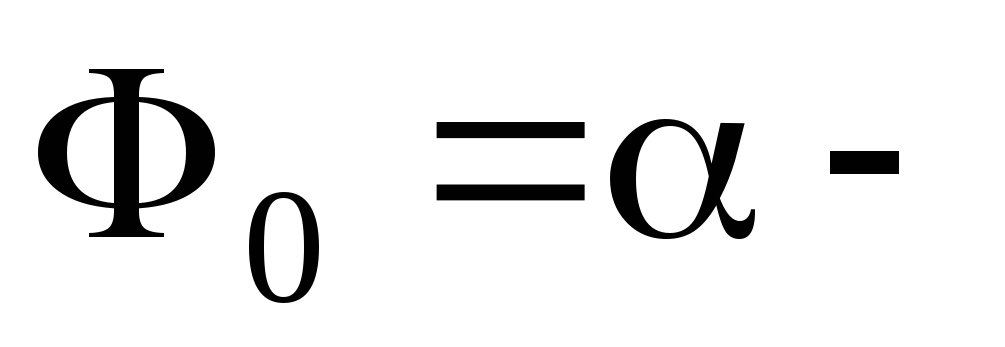 початкова фаза,
початкова фаза,
частота коливань
![]() ,
(3)
,
(3)
період коливань
![]() ,
(4)
,
(4)
струм у колі
![]() . (5)
. (5)
Коливання струму випереджають коливання заряду за фазою на /2.
Напруга на обкладках конденсатора
![]()
![]() .
(6)
.
(6)
Напруга на соленоїді
![]() ,
(7)
,
(7)
![]() .
(8)
.
(8)
Величини
![]() та
та![]() ,
що фігурують в (6) та (8) називаються
реактивними опорами конденсатора та
індуктивності відповідно.
,
що фігурують в (6) та (8) називаються
реактивними опорами конденсатора та
індуктивності відповідно.
Електрична та магнітна енергії контуру задаються виразами
![]() .
(9)
.
(9)
![]() .
(10)
.
(10)
Зважаючи на те, що
![]() ,
,
магнітну енергію можна записати у вигляді
![]() .
(11)
.
(11)
Середні значення енергій <Wm> та <Wm> за період задаються виразами
![]() ,
(12)
,
(12)
![]() ,
(13)
,
(13)
де середнє значення косинуса є
![]()
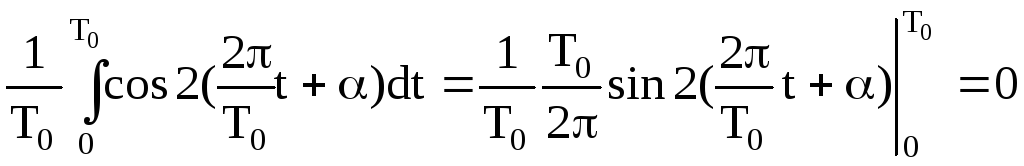 .
.
Таким чином одержимо
![]()
![]() ,
,
а повна енергія буде такою
![]() .
(14)
.
(14)
Під час коливань електрична енергія конденсатора (потенціальна енергія) переходить у магнітну енергію соленоїда (кінетична енергія) і навпаки так, що зберігається повна енергія контуру W.
Хвильовий опір контуру змінному струмові визначається так
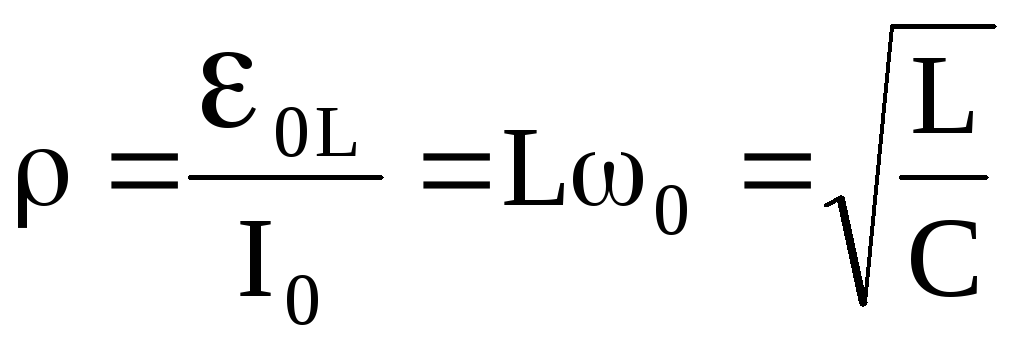 .
(15)
.
(15)
12.3. Вільні згасаючі електромагнітні коливання
1.
Вільні згасаючі електромагнітні
коливання виникають у RLC-контурі у тому
випадкові, коли в ньому відсутнє зовнішнє
джерело енергії (![]() ).
Рівняння цих коливань запишеться у
вигляді
).
Рівняння цих коливань запишеться у
вигляді
![]() ,
(1)
,
(1)
а його розв'язком є
![]() ,
(2)
,
(2)
де
=
![]() =
=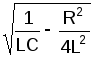 ,
=
,
=
![]() (3)
(3)
циклічна частота.
2. Характеристики згасаючих коливань
Амплітуда коливань є спадною функцією часу
А(t)=Aoe-t, (4)
Період коливань
![]() =
=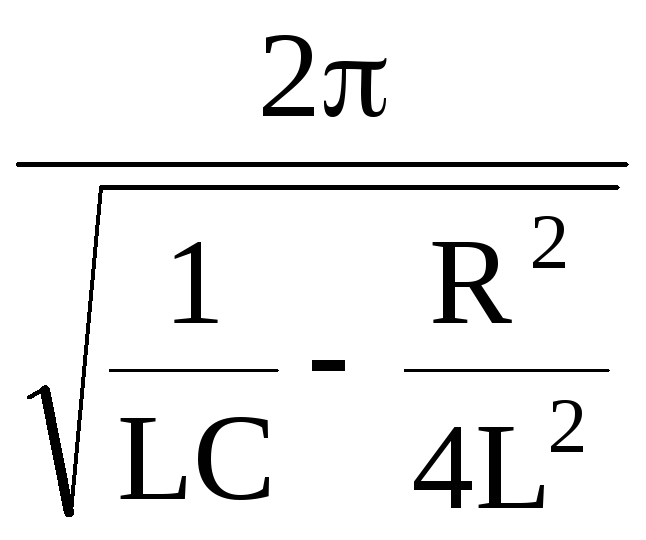 =
=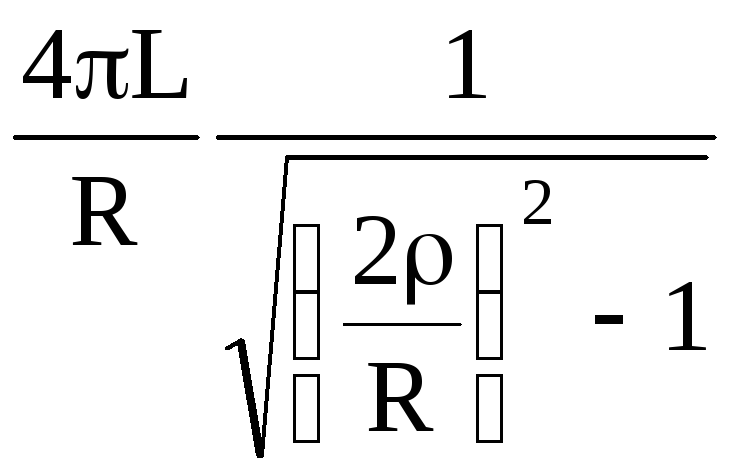 ,
(5)
,
(5)
час релаксації
![]() =
=![]() ,
(6)
,
(6)
число повних коливань за час релаксації
![]() ,
(7)
,
(7)
логарифмічний декремент згасання
 , (8)
, (8)
добротність контура
![]() ,
(9)
,
(9)
У випадку
малого опору R
(![]() ,
а
,
а![]() ), коли можна покласти
), коли можна покласти
![]()
![]() (10)
(10)
![]() =
=![]() .
(11)
.
(11)
Величина A2(t)-A2(t+T) пропорційна джоулевій теплоті, яка виділяється на опорі R контуру.
У випадку малого опору, коли
![]() добротність буде
добротність буде
![]() .
(12)
.
(12)
Повний опір контуру (імпеданс) визначається так
![]() .
(13)
.
(13)
