11.8.3. Потокозчеплення.

Повний магнітний потік через N простих контурів із магнітним потоком Ф через кожний з них називається потокозчепленням. Наприклад, магнітний потік через виток соленоїда з перерізом S і лінійною густиною n витків є

, (5)

а потокозчеплення через N витків становить

, (6)

де V  об'єм соленоїда.

Потокозчеплення контуру, зумовлене магнітним полем струму, що тече в іншому контурі називається потокозчепленням взаємної індукції цих контурів.

11.8.4. Робота по переміщенню провідника із струмом у магнітному полі.

Якщо в магнітному полі з індукцією знаходиться провідник dl із струмом І, то магнітне поле створить силу Ампера(див.Мал.118). Ця сила приведе провідник у рух і за час dt він переміститься на. Елементарну роботу сили Ампера запишемо у вигляді

,

звідки маємо

А = IdФ, (7)

де вектор малої площадки, яку пересікає провідник, магнітний потік, який перетинає провідник за час руху.

Якщо провідник пересікає поверхню S, через яку протікає магнітний потік , то роботу можна визначити так

. (8)

11.9. Визначення питомого заряду електрона

Питомий заряд електрона

(1)

м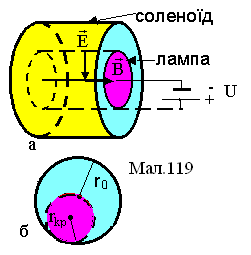ожна визначити, розглядаючи його рух у схрещених (взаємно перпендикулярних) магнiтному та електричному полях. Такі поля можуть створювати, наприклад, соленоїд та циліндрична електронна лампа, розміщена в ньому (див.Мал.119а). Така конфігурація називається магнетроном і її назва зв'язана з тим, що вона нагадує конфігурацію полів у магнетронах (генераторах електромагнітних коливань в області надвисоких частот). Анодом лампи є циліндр радіуса, а катодом - розжарена нитка, розміщена вздовж осі циліндра.Проходячи анодну напругу U, термоелектрони катода наблизяться до поверхні анода і набудуть швидкість V. Робота електричного поля А=еU йде на створення кінетичної енергії електрона

. (2)

При цьому, маючи швидкість V, електрон під дією сили Лоренця (доцентрової) рухається при поверхні анода по колу, а рівняння другого закону Ньютона буде мати вигляд

. (3)

Розв'язок системи рівнянь (2)-(3) відносно  проведемо так: із рівняння (3) визначимо

і підставимо у (2)

.

Після скорочення одержимо

, (4)

де індукція поля соленоїда . Збільшуючи струм соленоїда при сталій напрузіU, можна знайти такий критичний струм І_кр соленоїда, коли при подальшому збільшенні його, анодний струм почне зменшуватися. Таке зменшення анодного струму пов'язане з тим, що при цьому частина електронів почне рухатися по колу з радіусом (див.Мал.119б) і не досягатиме поверхні анода. Тепер (4) можна записати у вигляді

. (5)

11.10. Ефект Холла

Нехай металевий провідник чи напівпровідник у формі паралелепіпеда довжини L, ширини b та висотою d знаходиться в магнітному полі з індукцією (див.Мал.120). До провідника прикладена напругаU, що створює в ньому напруженість поля та струм І. Ефект Холла полягає у тому, що при протіканні струму І через провідник, між верхньою та нижньою гранями створюється напруга U_, яку називають поперечною або холлівською. Холл дослідним шляхом установив залежність величини від густини струму та індукції В

U, (1)

д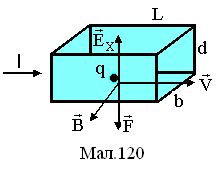е величина  стала Холла.

Для розгляду ефекту Холла на основі електронної теорії провідності, зробимо декілька попередніх зауважень. Покладемо, що носіями струму є додатні заряди q, які рухаються із середньою швидкістю направленого руху і мають концентраціюn.

При протіканні струму І через провідник, додатні носії струму q під дією сили Лоренця рухаються до нижньої основи. Накопичення заряду на нижній основі створює поперечне електричне поле з напруженістю. Напруженість поля сили Лоренця дорівнює. При цьому поперечна напруга, яку створює поле сторонніх сил, дорівнює

. (2)

Підставивши в (2) значення середньої швидкості V = j/qn, одержимо

. (3)

У цьому виразі стала Холла дорівнює

. (4)

Густину струму j=nqV можна записати через рухливість u=V/E у вигляді j=nquE. Зважаючи на диференціальний закон Ома , депитомий опір провідника, можна знайти вираз для рухливості носіїв струму

. (5)

Таким чином рухливість зарядів можна записати через сталу Холла та питомий опір провідника  у вигляді

. (6)

У нашому досліді питомий опір можна знайти з того, що прикладена напруга до провідника U створює струм І, а тому R=U/I. З іншого боку, R=L/(bd) i таким чином одержимо

. (7)