11.5. Закон Ампера, сила Лоренця

Проводячи цілий ряд дослідів, Ампер установив, що на елемент провідника із струмом І в магнітному полі з індукцієюдіє сила

. (1)

Струм в елементі провідника dl створюють dN електронів із зарядомq=е. Електрони рухаються з дрейфовою швидкістю , причому. Підставляючи І та dl у формулу дляодержимо

.

З одержаного виразу знайдемо силу, що діє на рухомий заряд q

. (2)

Сила називається магнітною складовою сили Лоренця - сили, що діє на заряджену частинку в електромагнітному полі

, (3)

де електрична складова сили Лоренця, напруженість електричного поля. Силаперпендикулярна векторамі, тому є доцентровою силою, яка викликає рух заряду по колу з радіусом R. Площина кола є площиною векторів та(див. Мал.114). Нехай. Доцентрове прискорення за величиною дорівнює, а рівняння Ньютоназапишемо у вигляді

(4)

звідки

. (5)

Період обертання для рівномірного руху заряду в однорідному магнітному полі зі сталою індукцією можна знайти, розділивши довжину кола С = 2R на швидкість обертання V

. (6)

З одержаного виразу видно, що період обертання не залежить від швидкості частинки. Якщо вектор швидкості заряду не перпендикулярний вектору індукції магнітного поля і має складові та , то заряд рухається по колу з радіусом. При цьому частинка буде описувати гвинтову лінію з кроком

. (7)

11.6. Сила взаємодії струмів

Нехай маємо два нескінченно довгі паралельні провідники (див.Мал. 115) із струмамита, відстань між якими b (b>>l - довжини провідників). В околиці елемента dl струму І₂ струм І₁ створює магнітне поле з індукцією величини

. (1)

Якщо напрямок струму І₁ співпадає з віссю ОХ і струми лежать у площині ХОУ, то вектор у будь - якій точці струму І₂ направлений по осі ОZ. Сила Ампера, що діє на елемент провідника dl визначається законом Ампера

. (2)

Вектор направлений до струму. Якщо струми паралельні, то провідники притягуються, а коли навпаки, то провідники відштовхуються. У явному вигляді, після підстановки величини В (), сила взаємодії запишеться у вигляді

. (3)

11.7. Потенціальна енергія контуру в магнітному полі

11.7.1. Момент сили, що діє на контур.

На контур із струмом I, що знаходиться в магнітному полі з індукцією діє пара сил із плечем а (див. Мал.116). Вони створюють момент сили, який можна записати так

(1)

з величиною

, (2)

де магнітний момент контуру, S = ab.

11.7.2. Енергія контуру.

При повороті контуру на кут момент сили виконує роботу, а повна робота

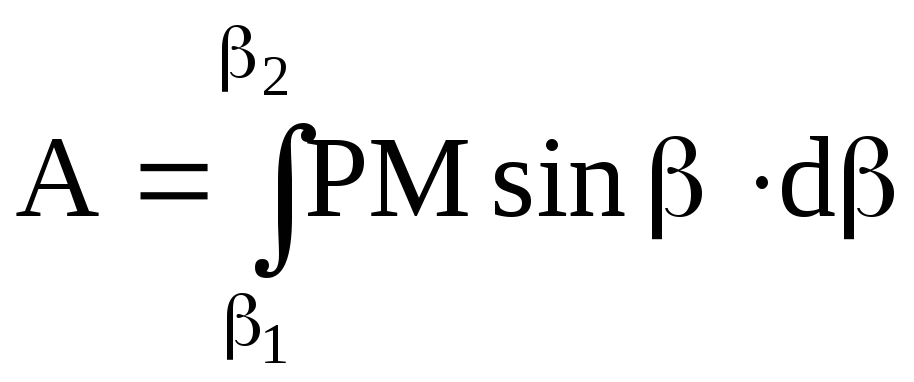, (3)

де  - кут між векторами та , інтегрування проводиться від до. Після інтегрування маємо

. (4)

Ця робота виконується за рахунок зменшення потенціальної енергії взаємодії контуру з магнітним полем

, (5)

де величина

(6)

• є механічна потенціальна енергія контуру в магнітному полі.

11.8. Потік індукції магнітного поля

11.8.1. Потік вектора магнітної індукції

Елементарний потік dФ вектора індукції магнітного поля через елементарну поверхню dS із нормаллю (див.Мал.117) визначається скалярним добутком

, (1)

де вектор.

Потік через деяку незамкнену поверхню є

. (2)

11.8.2. Теорема Остроградського-Гауса для магнітного поля.

Потік вектора магнітної індукції через довільну замкнену поверхню S за теоремою Остроградського-Гауса дорівнює нулю

. (3)

Цей результат відображає той факт, що в природі досі не знайдено магнітних зарядів (монополів Дірака), які були б джерелами магнітного поля і на яких починались чи закінчувались силові лінії. На відміну від електростатичного поля такі поля називаються соленоїдальними і вони не є потенціальними. Для доведення теореми Остроградського-Гауса (3) запишемо і, виходячи з визначення силової лінії магнітного поля ((4) §33), маємо, деdN  число силових ліній, що пронизують поверхню dS_. Тепер

, (4)

де N₊  силові лінії, що виходять через поверхню S, а N_  силові лінії, що входять через неї. В силу замкненості силових ліній і тому

.