Введение

В связи с внедрением кредитно-модульной системы в процесс обучения изменился подход к организации работы со студентами.

Самостоятельная работа студентов является основным методом усвоения учебного материала в рамках кредитно-модульной системы обучения.

Целью данного учебного пособия является оказание помощи студентам в освоении таких тем как “Пределы” и “Дифференциальное исчисление”.

Для успешного изучения материала студенты должны освоить теоретический материал, разобрать решенные задачи и для закрепления изученного теоретического материала выполнить индивидуальные задания.

Тестовые задания содержат 30 вариантов (с выборочными ответами) и охватывают теоретические положения, изложенные в данной разработке.

Данное пособие может быть использовано для индивидуальной работы студентов других специальностей дневного и заочного отделений.

I. Теория пределов Основные понятия

Если каждому натуральному числу поставлено в соответствие число, то говорят, что данапоследовательность или короче: последовательность.

Общий член последовательности является функцией натурального аргумента, т.е..

Число называетсяпределом последовательности , если для любого положительного числанайдется такой номер, что для всехвыполняется неравенство

.

Последовательность называетсябесконечно большой, если для любого числа найдется номер, такой, что для всехвыполняется неравенство.

Последовательность называетсябесконечно малой, если .

Если последовательность бесконечно малая и все ее члены отличны от нуля, то последовательность– бесконечно большая, и обратно, если последовательность– бесконечно большая, то последовательность– бесконечно малая.

Предел функции

1.2.1. Основные понятия

Пусть функция определена в некоторой окрестности точки, кроме, быть может, в самой точке.

Число называетсяпределом функции при , стремящемся к, если для любого положительного числанайдется такое положительное число, что для всех, удовлетворяющих условию, выполняется неравенство, т.е.

.

1.2.2. Основные свойства о пределах функции

1. Предел постоянной равен этой постоянной: .

2. .

3. .

4. при условии, что .

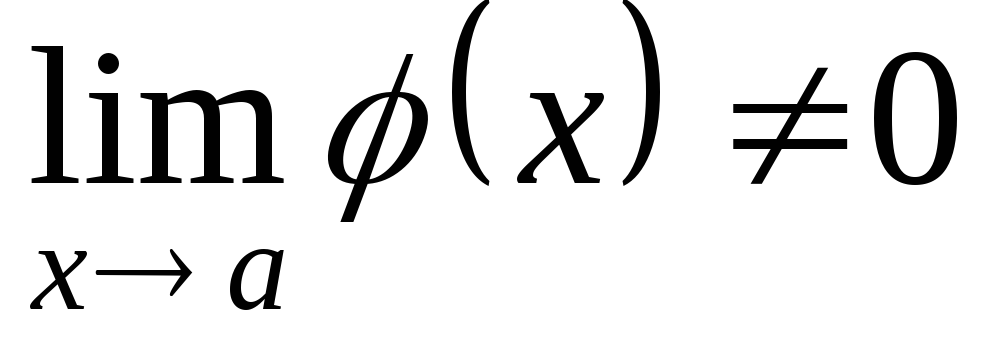1.2.3. Раскрытие неопределенностей

При нахождении предела подстановка в заданное выражение предельного значения аргумента часто приводит к неопределенным выражениям вида . Нахождение предела функции в этих случаях называется раскрытием неопределенности, для этого следует проводить преобразования данного выражения.

Техника вычисления пределов

а) Предел отношения многочленов ипри стремлении аргумента к бесконечности (неопределенность) находят путем почленного деления числителя и знаменателя на старшую степень, при этом получают:

Пример 1.1. Найти .

Решение. Разделим числитель и знаменатель дроби на :

,

т.к. ;;.

б) Для раскрытия неопределенности следует выделить критический множитель (множитель, предел которого равен нулю) и сократить.

Пример 1.2. Найти .

Решение.

.

в) Если при раскрытии неопределенности выражение имеет иррациональность, надо перенести эту иррациональность из числителя в знаменатель или из знаменателя в числитель, выделить критический множитель и сократить.

Пример 1.3. Найти .

Решение.

г) Если при раскрытии неопределенности выражение содержит тригонометрические функции, то следует использовать первый замечательный предел:

Пример 1.4. Найти .

Решение.

.

д) Неопределенность раскрывают приведением к общему знаменателю или домножением на сопряженное выражение.

Пример 1.5. Найти .

Решение.

е) Для раскрытия неопределенности используется второй замечательный предел:

или .

Пример 1.6. Найти .

Решение.

.