
- •Список принятых сокращений
- •Тема 1. Методы решения систем линейных уравнений
- •Лекция 1. Метод Гаусса
- •Концепция методов
- •Метод Гаусса
- •Верхняя треугольная система линейных уравнений
- •Метод исключения Гаусса и выбор главного элемента
- •Схема единственного деления
- •Лекция 2. Итерационные методы
- •Метод итераций
- •Замечания о точности расчета
- •Достаточное условие
- •Приведение линейной системы к виду удобному для итерации.
- •Метод Зейделя
- •Тема 2. Методы решения нелинейных уравнений
- •Лекция 3. Метод половинного деления
- •Приближенное решение нелинейных уравнений
- •Отделение корней
- •Метод половинного деления
- •Лекция 4. Метод Ньютона
- •Методика решения задачи
- •Ошибка деления на нуль.
- •Скорость сходимости.
- •Модификации метода Ньютона.
- •Упрощенный метод Ньютона
- •Метод Ньютона-Бройдена
- •Метод секущих
- •Тема 3. Численное интегрирование
- •Лекция 5. Метод трапеций
- •Постановка задачи
- •Формула трапеций
- •Погрешность формулы трапеций
- •Общая формула трапеций
- •Лекция 6. Метод Симпсона
- •Формула Симпсона
- •Остаточный член формулы Симпсона
- •Общая (обобщенная) формула Симпсона
- •Тема 4. Обработка экспериментальных данных
- •Лекция 7. Интерполирование
- •Постановка задачи
- •Линейная интерполяция
- •Квадратичная интерполяция
- •Интерполяционная формула Лагранжа.
- •Вычисление Лагранжевых коэффициентов
- •Интерполяция сплайном
- •Лекция 8. Метод наименьших квадратов
- •Постановка задачи
- •Метод наименьших квадратов
- •Линейная аппроксимация (интерполяция)
- •Коэффициент линейной корреляции
- •Квадратичная аппроксимация
- •Приложения
- •Транспонирование
- •Вычисление определителя матрицы
- •Нахождение обратной матрицы
- •Сложение и вычитание матриц
- •Умножение матрицы на число
- •Умножение матриц
- •Итерационные методы решения уравнений
- •Стандартные формы уравнений
- •Поиск корней графическим методом
- •Простой итерационный метод догадки и проверки
- •Представление уравнения в форме 2
- •Прямая подстановка
- •Итерации в ячейке
- •Введение в надстройку Поиск решения
- •Активирование надстройки Поиск решения
- •Установка надстройки Поиск решения
- •Применение надстройки Поиск решения
- •Приложение 3. Контрольные вопросы
- •Приложение 4. Список лабораторных работ
- •Часть 1. Вычислительная техника
- •Часть 2. Численные методы
- •Список литературы.
- •Основная литература
- •Дополнительная литература
- •Интернет-ресурсы
|
Лекция 4. Метод Ньютона |
|
|
|||||
Если f (x), |
f ' (x) и f '' (x) непрерывны в окрестности корня, эту допол- |
|||||||
нительную информацию о свойствах функции |
f (x) |
можно использовать для |
||||||
построения алгоритмов, которые порождают последовательности, сходящиеся к |
||||||||
корню быстрее, чем при методе деления пополам или методе ложного положе- |
||||||||
ния. Метод Ньютона-Рафсона (или просто Ньютона, также имеет названия |
||||||||
метод касательных и метод линеаризации) является одним из наиболее по- |
||||||||
лезных и самых известных алгоритмов, в котором используется непрерывность |
||||||||
f ' (x) и f '' (x). Он быстро сходится (имеет квадратичную сходимость) и до- |
||||||||
пускает различные модификации, приспособленные для решения векторных за- |
||||||||
дач и других уравнений. Однако, этот метод эффективен при весьма жестких |
||||||||
ограничениях на характер функции |
f (x): |
|
|
f (x) |
|
|
||
1. существование |
второй |
производной |
функции |
на |
множестве |
|||
G ={a ≤ x ≤ b}; |
|
|
|
f ' (x)≠ 0 для всех x G ; |
||||
2. удовлетворение первой производной условию |
||||||||
3. знакопостоянство f ' (x), |
f '' (x) |
для всех x G . |
|
|
|
|||
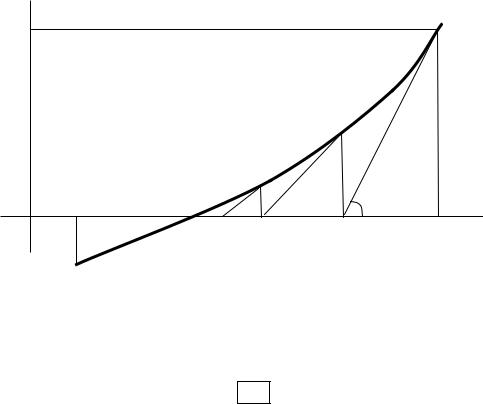
Геометрическая интерпретация метода Ньютона состоит в следующем. За- |
||||||||
дается начальное приближение x(0) . Далее проводится касательная к кривой |
||||||||
y = f (x) в точке x(0) (рис. 4.1), т.е. кривая заменяется прямой линией. В каче- |
||||||||
стве следующего приближения выбирается точка пересечения этой касательной |
||||||||
с осью абсцисс. Процесс построения касательных и нахождения точек пересе- |
||||||||
чения с осью абсцисс повторяется до тех пор, пока приращение не станет |
||||||||
меньше заданной величины ε . |
|
|
|
|
|
|
||
f (x(0) ) |
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
a |
C |
|
A |
α |
b |
|
||
|
|
|
||||||
0 |
|
x* |
x(2) |
|
x(1) |
|
x(0) |
|
Рис. 4.1 |
Геометрические построения для метода Ньютона |
|
||||||
29

Получим расчетную формулу метода Ньютона. Вместо участка кривой ВС (точка С соответствует x* ) возьмем участок АВ – касательную, проведенную в
точке (x(0) , f (x(0) )). Для этого отрезка справедливо конечное соотношение:
|
f (x(0) )− 0 |
|
= f ' (x |
(0) |
)≡ tgα |
(4.1) |
|||||||||||||
|
x |
(0) |
− x |
(1) |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где α - угол наклона касательной в точке (x(0) , f (x(0) )) к оси абсцисс. |
|||||||||||||||||||
Разрешая это соотношение относительно |
x(1), получаем: |
|
|||||||||||||||||
|
x |
(1) |
= x |
(0) |
− |
|
f (x(0) ) |
|
|
|
|
(4.2) |
|||||||
|
|
|
|
|
|
|
f ' (x(0) ) |
|
|
|
|
|
|||||||
Повторяя процесс, находим общую формулу: |
|
||||||||||||||||||
x |
(k |
+1) |
= x |
(k ) |
− |
f (x(k ) |
) |
|
, где k = 0,1,2,... |
(4.3) |
|||||||||
|
|
|
|
|
f ' (x(k ) ) |
|
|||||||||||||
Отметим, что если отбросить итерационный индекс, то (4.3) записывается в виде нелинейного уравнения:
x = x − |
f (x) |
≡ϕ(x) |
(4.4) |
|
f ' (x) |
||||
|
|
|
которое, однако, на [a,b] не равносильно исходному, а является таковым только в одной точке при x = x* . Поэтому данный метод не служит разновидностью
метода простых итераций.
Применим теперь для вывода формулы (4.3) метод линеаризации. Положим, что итерационный процесс имеет вид:
|
|
x(k+1) = x(k ) +δ (k ) , где k = 0,1,2,... |
(4.5) |
||
где δ (k ) |
- поправка к k -му приближению, которую необходимо найти. Предпо- |
||||
лагая, |
что |
f (x) имеет непрерывную вторую |
производную, |
разложим |
|
f (x(k ) +δ (k ) ) |
по формуле Тейлора относительно точки x(k ) : |
|
|||
|
f (x(k ) +δ (k ) )= f (x(k ) )+δ (k ) f ' (x(k ) )+ |
(δ (k ) )2 f "(ξ ) |
(4.6) |
||
где ξ (x(k ) , x(k+1) ). Учитывая, что f (x(k ) +δ (k ) ) |
2 |
|
|||
= 0 |
(это соответствует нахо- |
||||
ждению точки пересечения с осью абсцисс), и оставляя только линейную (относительно δ (k ) ) часть разложения (отсюда и название – метод линеаризации), записываем линейное относительно δ (k ) уравнение:
f (x(k ) )+δ (k ) f ' (x(k ) )= 0 |
(4.7) |
30
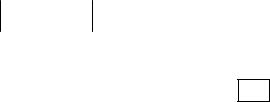
|
(k ) |
= − |
f (x(k ) ) |
δ |
(k ) |
|
|
Отсюда выражается поправка δ |
|
|
. Подставляя |
|
в (4.5), |
||
|
f ' (x(k ) ) |
|
|||||
получаем (4.3).
Замечания:
1)Из графика видно, что если начать строить касательные из точки а, то x(1) найдется вообще вне отрезка [a,b], где функция может быть даже не определена. Из простых рассуждений можно вывести правило выбора начальной
точки x(0) : в качестве исходной точки x(0) выбирается тот конец интервала [a,b], которому отвечает ордината того же знака, что и f "(x).
Или в виде формулы:
|
(0) |
|
|
|
x |
a, если f (a) f "(a)> 0 |
|||
|
= |
f (a) |
(4.8) |
|
|
|
b, если |
f "(a)< 0 |
|
|
|
|
|
|
2) Из графической аналогии метода ясно требование сохранения знаков f ' (x) и f "(x): функция на отрезке [a,b] не должна иметь перегибов и изменения
монотонности.
Теорема (о достаточных условиях сходимости метода Ньютона):
|
Пусть выполняются следующие условия: |
|
|
[a,b]. |
|||
1. |
Функция f (x) определена и дважды дифференцируема на участке |
||||||
2. |
Отрезку [a,b] |
принадлежит |
только |
один |
простой корень |
x* , |
так что |
|
f (a) f (b)< 0 . |
|
|
|
|
|
|
3. |
Производные f ' (x), f "(x) на [a,b] |
сохраняют знак, и f ' (x)≠ 0 . |
|
||||
4. |
Начальное |
приближение |
x(0) |
удовлетворяет |
неравенству |
||
|
f (x(0) ) f "(x(0) )> 0 (знаки функций f (x) |
и f "(x) в точке |
x(0) |
совпада- |
|||
ют).
Тогда с помощью метода Ньютона (4.3) можно вычислить корень уравнения f (x)= 0 с любой точностью ε .
Методика решения задачи
1. Задать начальное |
приближение |
x(0) |
так, чтобы выполнялось неравенство |
f (x(0) ) f "(x(0) ) |
> 0 , а также |
малое |
положительное число ε . Положить |
k= 0 .
2.Вычислить x(k+1)
3.Если x(k+1) − x(k ) ложить k = k + 1
по формуле x |
(k+1) |
= x |
(k ) |
− |
f (x(k ) ) |
|
|
|
|
. |
|||
|
|
f ' (x(k ) ) |
||||
≤ ε , процесс завершить и положить x* x(k+1) , иначе по- и перейти к пункту 2.
31
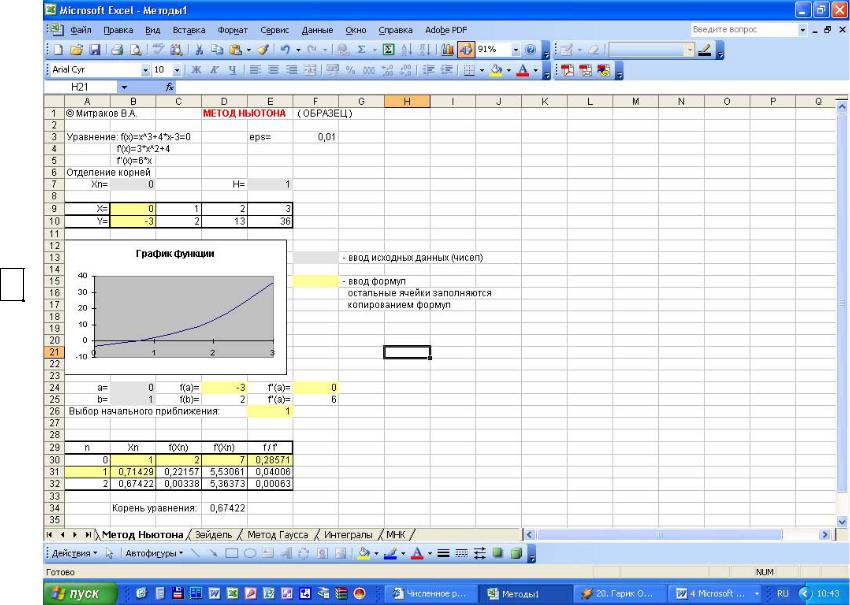
Пример 1 решения представлен на рис. 4.2.
32
Рис.4.2 Пример расчета по методу Ньютона.
