
- •Список принятых сокращений
- •Тема 1. Методы решения систем линейных уравнений
- •Лекция 1. Метод Гаусса
- •Концепция методов
- •Метод Гаусса
- •Верхняя треугольная система линейных уравнений
- •Метод исключения Гаусса и выбор главного элемента
- •Схема единственного деления
- •Лекция 2. Итерационные методы
- •Метод итераций
- •Замечания о точности расчета
- •Достаточное условие
- •Приведение линейной системы к виду удобному для итерации.
- •Метод Зейделя
- •Тема 2. Методы решения нелинейных уравнений
- •Лекция 3. Метод половинного деления
- •Приближенное решение нелинейных уравнений
- •Отделение корней
- •Метод половинного деления
- •Лекция 4. Метод Ньютона
- •Методика решения задачи
- •Ошибка деления на нуль.
- •Скорость сходимости.
- •Модификации метода Ньютона.
- •Упрощенный метод Ньютона
- •Метод Ньютона-Бройдена
- •Метод секущих
- •Тема 3. Численное интегрирование
- •Лекция 5. Метод трапеций
- •Постановка задачи
- •Формула трапеций
- •Погрешность формулы трапеций
- •Общая формула трапеций
- •Лекция 6. Метод Симпсона
- •Формула Симпсона
- •Остаточный член формулы Симпсона
- •Общая (обобщенная) формула Симпсона
- •Тема 4. Обработка экспериментальных данных
- •Лекция 7. Интерполирование
- •Постановка задачи
- •Линейная интерполяция
- •Квадратичная интерполяция
- •Интерполяционная формула Лагранжа.
- •Вычисление Лагранжевых коэффициентов
- •Интерполяция сплайном
- •Лекция 8. Метод наименьших квадратов
- •Постановка задачи
- •Метод наименьших квадратов
- •Линейная аппроксимация (интерполяция)
- •Коэффициент линейной корреляции
- •Квадратичная аппроксимация
- •Приложения
- •Транспонирование
- •Вычисление определителя матрицы
- •Нахождение обратной матрицы
- •Сложение и вычитание матриц
- •Умножение матрицы на число
- •Умножение матриц
- •Итерационные методы решения уравнений
- •Стандартные формы уравнений
- •Поиск корней графическим методом
- •Простой итерационный метод догадки и проверки
- •Представление уравнения в форме 2
- •Прямая подстановка
- •Итерации в ячейке
- •Введение в надстройку Поиск решения
- •Активирование надстройки Поиск решения
- •Установка надстройки Поиск решения
- •Применение надстройки Поиск решения
- •Приложение 3. Контрольные вопросы
- •Приложение 4. Список лабораторных работ
- •Часть 1. Вычислительная техника
- •Часть 2. Численные методы
- •Список литературы.
- •Основная литература
- •Дополнительная литература
- •Интернет-ресурсы

Тема 2. Методы решения нелинейных уравнений1
Лекция 3. Метод половинного деления
Приближенное решение нелинейных уравнений
Для достаточно сложных алгебраических и трансцендентных уравнений не всегда можно найти точное решение, поэтому очень часто приходится применять приближенные (численные) методы нахождения корней таких уравнений.
Пусть дано нелинейное уравнение
f (x)= 0 |
(3.1) |
Где f (x) – функция определённая и непрерывная на некотором (даже бесконечном) интервале a < x < b. В некоторых случаях на функцию f (x) могут
быть наложены дополнительные ограничения, например, непрерывность первой и второй производных, что специально оговаривается.
Требуется найти корни уравнения (3.1). Т.е. Числа x*1 , x*2 ,..., которые путем подстановки их в (3.1) превращают уравнение в верное числовое равенство. Числа x*1 , x*2 ,... также называются нулями функции f (x).
Определение 1 корнем уравнения (3.1) называется значение x = x* , обращающее функцию f (x) в ноль, т.е. f (x* )≡ 0 .
Определение 2 изолированный корень – это значение x , удовлетворяющее (3.1) и не содержащее других корней в своей окрестности.
Условие существования корня уравнения (3.1) следует из теоремы:
Если непрерывная функция f (x) принимает значения разных знаков на концах отрезка [a,b], т.е. f (a) f (b)< 0 , то внутри этого отрезка содержится, по крайней мере, один корень уравнения f (x)= 0 . Значит, найдется хотя бы одно число x* (a,b) такое, что f (x* )= 0 . Если же f (x) непрерывна и дифференцируема и ее первая производная сохраняет знак внутри отрезка
[a,b], то на данном отрезке находится только один (изолированный) корень
x= x* уравнения.
Таким образом, при нахождении корней уравнения (3.1) численным методом, кроме непрерывности f (x) предполагается:
1.Функция принимает на концах отрезка разные знаки;
2.Производные f ' (x) и f "(x) непрерывны на отрезке;
3.Производные на отрезке не меняют знака.
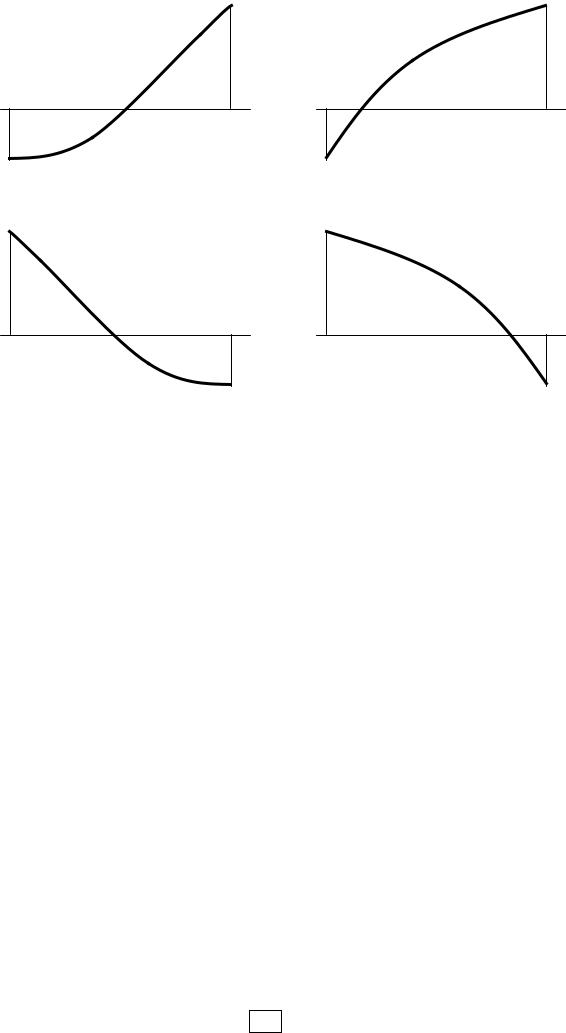
Геометрически последнее условие означает, что предполагается одна из четырех схем (рис. 3.1).
1 В приложении 2 рассмотрены способы решения уравнений с помощью итерационных методов
23
а |
b |
а |
b |
а |
b |
а |
b |
Рис. 3.1. Геометрическая трактовка знакопостоянства производных
Приближенное нахождение изолированных действительных корней уравнения (3.1) осуществляется в два этапа:
1.Находятся отрезки ai ,bi , внутри каждого из которых содержится один и только один корень уравнения. Этот этап называется процедурой отделения корней. По сути, на нем осуществляется грубое нахождение корней x = x*i .
2.Грубое значение каждого корня x = x*i уточняется до заданной точности од-
ним из численных методов, в которых реализуются последовательные приближения.
Первый этап значительно сложнее второго. Так как не существует достаточно эффективных методов отделения всех корней. Чаще всего используют следующие способы нахождения отрезков изоляций: графический (с помощью построения и исследования графиков функций); аналитический (основан на подробном исследовании функции); метод последовательного перебора (основан на вычислении функции с заданным шагом аргумента и выделении тех отрезков, где функция меняет знак).
Отделение корней
Отделение корней начинается с установления знаков f (x) в граничных
точках области определения функции.
После этого, либо аналитически, либо графически, используя особенности функции, находят значения функции в некоторых промежуточных точках x = x1 , x2 ,... и выбирают интервалы, в которых функция имеет разные знаки на
концах интервала. По условиям вышеизложенной теоремы в таких интервалах существует корень уравнения.
24
После этого необходимо убедится в том, что в каждом интервале находится только один корень. В противном случае изменять интервал.
Замечание 1: если известны корни уравнения f ' (x)= 0 , то процесс отделения корней можно упростить. Для этого достаточно определить знаки функции f (x) в точках нулей ее производной f ' (x)= 0 и граничных точках определения функции x = a и x = b .
Замечание 2: действительные корни уравнения f (x)= 0 можно отделить приближенно, как точки пересечения графиком y = f (x) оси абсцисс.
Этот метод удобен своей наглядностью, но при вычислениях вручную им не всегда можно воспользоваться, поскольку:
1. f (x) представляет собой функцию, график которой построить сложно (например, y = ex + sin x ).
2.Ограниченность размеров чертежа позволяет найти корни только в некотором ограниченном промежутке.
Первый недостаток можно устранить, если удается записать исходное
уравнение f (x)= 0 в виде ϕ(x)= g(x), при котором y =ϕ(x) и y = g(x) построить значительно проще. Тогда корни уравнения находятся как абсциссы точек пересечения графиков y =ϕ(x) и y = g(x).
Пример 1. Отделить корни уравнения: x ln x = 1
Решение. Запишем это уравнение в виде ln x = 1x . Построим графики и определим точку их пересечения (рис. 3.2).
2,5
2
1,5
1 |
|
Точка пересечения – корень урав- |
|
||
|
|
нения x ln x = 1 |
|
|
0,5
0 |
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
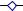 ln(x)
ln(x) 
 1/x
1/x
9
Рис. 3.2. Решение уравнения x ln x = 1.
Достоинством графического метода (кроме его наглядности) является то, что часто он дает возможность оценить количество корней и их знаки.
Перейдем ко второму этапу численного решения уравнений – уточнению корней до нужной точности. На этом этапе применяют несколько методов.
25

Метод половинного деления Иначе этот метод называют метод Больцано деления пополам или метод
бисекций. |
f (x)= 0 , имеется отрезок [a,b] изоляции корня x* |
|
Пусть дано уравнение |
||
для данного уравнения, |
f (x) непрерывна на отрезке |
[a,b]. Тогда график |
функции y = f (x) пересекает ось OX на отрезке [a,b] |
в точке x* и значения |
|
функции на концах отрезка имеют разные знаки, т.е. |
|
|
|
f (a) f (b)< 0 . |
(3.2) |
Отрезок [a,b], в данном случае, называется начальным интервалом не-
определенности, потому что известно, что корень ему принадлежит, но его местоположение с требуемой точностью не определено.
Основная идея метода бисекций: делим отрезок изоляции пополам и выбираем ту половину, где функция меняет знак, получаем новый отрезок изоляции, длина которого в два раза меньше предыдущего. Эту процедуру повторяем до тех пор, пока длина отрезка изоляции не станет меньше заданной точности. Рассмотрим это более подробно.
|
|
|
|
|
|
|
|
|
|
|
a + b |
|||||
|
Для нахождения корня делим отрезок [a,b] пополам. Если f |
|
2 |
= 0 , то |
||||||||||||
|
a + b |
|
|
|
|
|
|
|
|
|
|
|
|
|||
c = |
является корнем. Считаем, что |
f (c)≠ 0 . Тогда выберем ту из полови- |
||||||||||||||
|
||||||||||||||||
2 |
|
a + b |
a + b |
|
|
|
|
|
|
|
|
|
||||
|
|
|
, на концах которой функция имеет разные |
|||||||||||||
нок отрезка a; |
2 |
|
или |
2 |
;b |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b − a |
|
|||
знаки, и обозначим этот отрезок a |
;b |
. Длина этого отрезка: b − a |
|
= |
. |
|||||||||||
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отрезок a1 ;b1 снова делим пополам и выбираем новый отрезок a2 ;b2 аналогично. Строим последовательность отрезков an ;bn , каждый из которых вдвое меньше предыдущего, т.о. Получим последовательность вложенных друг в друга промежутков ai ;bi таких, что f (ai ) f (bi )< 0 (i = 1,2,3,...,n).
Этот процесс последовательного деления пополам продолжаем до тех пор, пока не выполнится одно из двух условий:
1.Либо найдется такая точка cn = an +2 bn , в которой f (cn )= 0 и cn – точное значение корня (на практике получается достаточно редко).
2.Либо на некотором шаге получим отрезок изоляции an ;bn , длина которого меньше требуемой точности:
b |
− a |
|
= b − a |
< ε |
(3.3) |
n |
|
n |
2n |
|
|
Левые концы отрезков образуют монотонную неубывающую последовательность an , а правые – bn , образуют монотонную невозрастающую последо-
26

вательность. Следовательно, эти последовательности имеют один и тот же предел x* :
x* = lim an = lim bn
n→∞ n→∞
Подставляя x* в (3.2) перейдем к пределу. Получим
lim f (an ) f (bn )= f (x* ) f (x* )< 0 .
n→∞
Это противоречие, значит f (x* )= 0 .
Так как корень принадлежит отрезку изоляции an ;bn . То в этом случае,
любое число из этого отрезка отличается от точного значения корня меньше, чем на ε . Числа an и bn являются приближенными значениями искомого корня
с недостатком и избытком соответственно. Обычно берут в качестве ответа число из середины последнего отрезка изоляции:
x* = |
an + bn |
= cn |
(3.4) |
|
|||
2 |
|
|
|
Можно заранее оценить количество делений пополам исходного отрезка. Так как каждый раз длина отрезка уменьшается в два раза, то по достижении
требуемой точности ε за n шагов получим отрезок длиной
Отсюда можно выразить, прологарифмировав, n:
lg b − a n > ε lg 2
Или
n > lg (lgb −2 a) − lglgε2
bn − an = b2−na < ε .
(3.5)
(3.6)
Из этой формулы можно оценить количество шагов. Кроме того, из нее видно, что для того, чтобы улучшить точность в k раз, т.е. Положив ε* = εk ,
необходимо сделать дополнительно n1 > lglg k2 шагов.
Основным достоинством метода бисекций является надежность, устойчивость к ошибкам округления, отсутствие ограничений на вид функции f (x)
(требуется только непрерывность). Главный недостаток – медленная сходимость к точному решению.
На практике метод бисекций используют в комбинации с каким-либо быстросходящимся методом: методом бисекций вначале грубо определяют начальное приближение, азатемприменяютбыстросходящийсяметод(например, методНьютона).
Пример реализации метода половинного деления в среде Microsoft Excel представлена на рис. 3.3.
27

28
Рис. 3.3
Пример расчета по методу половинного деления в
Microsoft Excel
