к которой можно применить метод итераций.

Метод Зейделя

Метод Зейделя представляет собой некоторую модификацию метода итераций. Основная идея метода состоит в том, что при вычислении (k + 1)-го

приближения неизвестной xi учитывать уже вычисленные (k + 1)-е приближения неизвестных x1 , x2 ,...,xi−1 .

Пусть дана приведенная система линейных уравнений:

j=1

Выбираем начальное приближение (разумное): x1(0) , x2(0) ,..., xn(0)

Далее предполагая, что k -е приближение известно, будем строить (k + 1)-е приближение корней по следующим формулам:

j=1

Или в развернутом виде:

x1(k+1) =α11 x1(k ) +α12 x2(k ) +α13 x3(k ) + ...+α1n xn(k ) + β1

x2(k+1) =α21 x1(k+1) +α22 x2(k ) +α23 x3(k ) + ...+α2n xn(k ) + β2

(2.8)

x3(k+1) =α31 x1(k+1) +α32 x2(k+1) +α33 x3(k ) + ...+α3n xn(k ) + β3

M

xn(k+1) =αn1 x1(k+1) +αn2 x2(k+1) +αn3 x3(k+1) + ...+αnn−1 xn(k−+11) +αnn xn(k ) + βn

20

Отметим, что указанная выше теорема сходимости для метода итераций остается верной и для метода Зейделя.

Обычно, но не всегда, метод Зейделя дает лучшую сходимость Пример 3. Методом Зейделя решить систему уравнений:

10 x1 + x2 + x3 = 122 x1 + 10 x2 + x3 = 13

2 x1 + 2 x2 + 10 x3 = 14

Приведем систему к виду, удобному для итераций:

x1 = 1,2 − 0,1 x2 − 0,1 x3x2 = 1,3 − 0,2 x1 − 0,1 x3x3 = 1,4 − 0,2 x1 −0,2 x2

В качестве нулевых приближений корней возьмем:

Применяя метод Зейделя последовательно получим: Первый шаг:

x1 = 1,2 − 0,1 0 − 0,1 0 = 1,2

x2 = 1,3 − 0,2 1,2 − 0,1 0 = 1,06

x3 = 1,4 − 0,2 1,2 − 0,2 1,06 = 0,948

Второй шаг:

x1 = 1,2 − 0,1 1,06 − 0,1 0,948 = 0,9992

x2 = 1,3 − 0,2 0,9992 − 0,1 0,948 = 1,00536

x3 = 1,4 − 0,2 0,9992 − 0,2 1,00536 = 0,999098

и т.д.

Результаты вычислений с точностью до четырех знаков приведены в таблице 2.2

Таблица 2.2 Вычисление решения системы линейных уравнений методом Зейделя

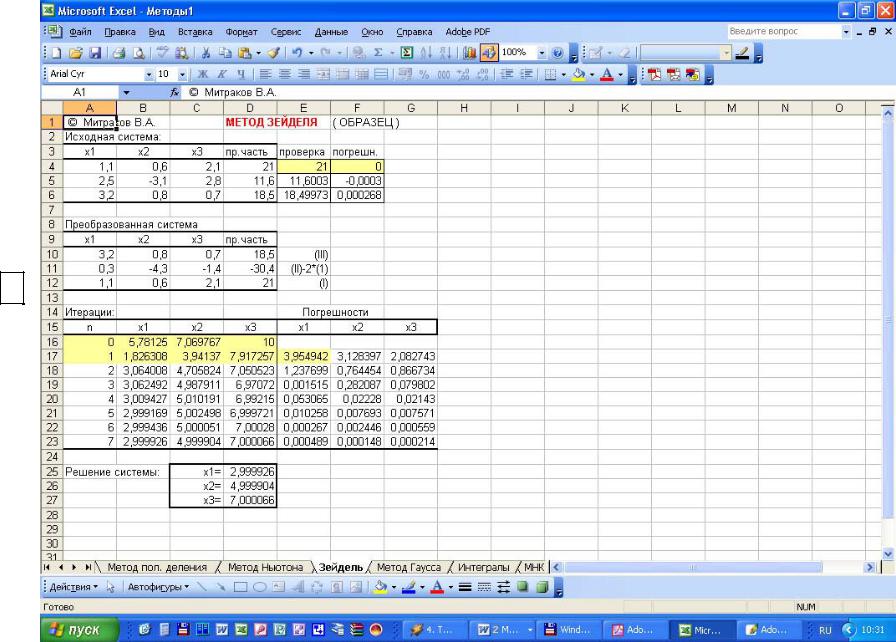
Точные значения корней: x1 = 1 , x2 = 1, x3 = 1 Пример расчета представлен на рис. 2.1

21