
- •Список принятых сокращений
- •Тема 1. Методы решения систем линейных уравнений
- •Лекция 1. Метод Гаусса
- •Концепция методов
- •Метод Гаусса
- •Верхняя треугольная система линейных уравнений
- •Метод исключения Гаусса и выбор главного элемента
- •Схема единственного деления
- •Лекция 2. Итерационные методы
- •Метод итераций
- •Замечания о точности расчета
- •Достаточное условие
- •Приведение линейной системы к виду удобному для итерации.
- •Метод Зейделя
- •Тема 2. Методы решения нелинейных уравнений
- •Лекция 3. Метод половинного деления
- •Приближенное решение нелинейных уравнений
- •Отделение корней
- •Метод половинного деления
- •Лекция 4. Метод Ньютона
- •Методика решения задачи
- •Ошибка деления на нуль.
- •Скорость сходимости.
- •Модификации метода Ньютона.
- •Упрощенный метод Ньютона
- •Метод Ньютона-Бройдена
- •Метод секущих
- •Тема 3. Численное интегрирование
- •Лекция 5. Метод трапеций
- •Постановка задачи
- •Формула трапеций
- •Погрешность формулы трапеций
- •Общая формула трапеций
- •Лекция 6. Метод Симпсона
- •Формула Симпсона
- •Остаточный член формулы Симпсона
- •Общая (обобщенная) формула Симпсона
- •Тема 4. Обработка экспериментальных данных
- •Лекция 7. Интерполирование
- •Постановка задачи
- •Линейная интерполяция
- •Квадратичная интерполяция
- •Интерполяционная формула Лагранжа.
- •Вычисление Лагранжевых коэффициентов
- •Интерполяция сплайном
- •Лекция 8. Метод наименьших квадратов
- •Постановка задачи
- •Метод наименьших квадратов
- •Линейная аппроксимация (интерполяция)
- •Коэффициент линейной корреляции
- •Квадратичная аппроксимация
- •Приложения
- •Транспонирование
- •Вычисление определителя матрицы
- •Нахождение обратной матрицы
- •Сложение и вычитание матриц
- •Умножение матрицы на число
- •Умножение матриц
- •Итерационные методы решения уравнений
- •Стандартные формы уравнений
- •Поиск корней графическим методом
- •Простой итерационный метод догадки и проверки
- •Представление уравнения в форме 2
- •Прямая подстановка
- •Итерации в ячейке
- •Введение в надстройку Поиск решения
- •Активирование надстройки Поиск решения
- •Установка надстройки Поиск решения
- •Применение надстройки Поиск решения
- •Приложение 3. Контрольные вопросы
- •Приложение 4. Список лабораторных работ
- •Часть 1. Вычислительная техника
- •Часть 2. Численные методы
- •Список литературы.
- •Основная литература
- •Дополнительная литература
- •Интернет-ресурсы
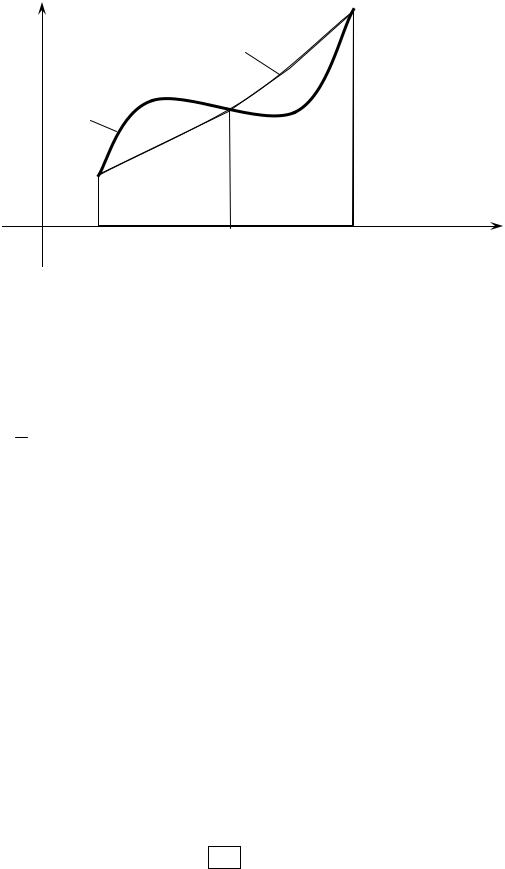
Лекция 6. Метод Симпсона
Геометрически формула Симпсона получается в результате замены подынтегральной функции y = f (x) параболой y = L2 (x), проходящей через три
точки M0 (x0 , y0 ), M1 (x1 , y1 ) и M2 (x2 , y2 ) (рис. 6.1).
M2 (x2 , y2 )
L2 (x)
M1 (x1 , y1 )
f (x)
M0 (x0 , y0 )
Рис. 6.1 Геометрические построения для метода Симпсона
Формула Симпсона
Из вида остаточного члена (5.15) следует, что результат, полученный по формуле трапеций, можно уточнять методом Рунге. Проводя такое уточнение для отрезка, содержащего узлы x0 , x1 , x2 , получим формулу Симпсона.
F ≈ 13 4 Fтрап (h)− Fтрап (2 h) =
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
= |
|
4 |
h |
|
f0 |
+ |
f1 |
+ |
|
f2 |
|
− 2 h |
|
f0 |
+ |
|
f |
2 |
|
= |
(6.1) |
|
3 |
2 |
2 |
2 |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
1 |
h |
( f0 + 4 f1 + |
f2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где h = xi |
− xi−1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Остаточный член формулы Симпсона
Таким образом, остаточный член формулы Симпсона равен:
x |
ydx − h |
|
|
R = ∫2 |
(y0 + 4 y1 + y2 ), где y = f (x) |
(6.2) |
|
x0 |
3 |
|
|
|
|
|
Предполагаем, что функция y C(4) [a,b], получим более простое выражение и для формулы Симпсона. Фиксируем среднюю точку x1 и рассматривая R = R(h), будем иметь:
43

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 +h |
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
= ∫ ydx |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.3) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
y(x1 − h)+ 4 y(x1 )+ y |
(x1 + h) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 −h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R = R(h) по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Отсюда, |
|
дифференцируя функцию |
|
h последовательно три |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
раза, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
R |
(h)= y(x1 + h) |
+ y(x1 − h) |
|
3 |
y(x1 − h)+ 4 y(x1 ) |
+ y(x1 + h) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||
|
|
|
− |
|
|
|
|
|
′ |
(x1 |
|
′ |
(x1 |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
y(x1 )− |
(6.4) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
−y |
|
− h)+ y |
+ h) |
3 |
|
|
y |
(x1 + h)+ y(x1 − h) |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
− |
h |
|
|
|
|
|
′ |
(x1 |
|
′ |
(x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
3 |
|
|
−y |
|
− h)+ y |
+ h) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
′′ |
(h)= |
|
|
|
|
|
|
′ |
(x1 − h)+ |
|
|
|
′ |
(x1 + h) |
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|||||||||||||||||||||||||||||||||||
|
R |
3 |
|
−y |
|
y |
|
3 |
|
|
−y |
(x1 − h)+ y |
|
(x1 + h) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
− |
h |
|
|
′′ |
(x1 − h)+ y |
′′ |
(x1 |
+ h) |
|
= |
1 |
|
|
|
|
|
′ |
(x1 − h)+ |
′ |
|
|
|
|
|
|
|
|
(6.5) |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
y |
|
|
|
|
|
3 |
|
−y |
y |
(x1 + h) − |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
− |
h |
|
|
′′ |
(x1 − h)+ y |
′′ |
(x1 |
+ h) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
3 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
′′′ |
|
|
|
|
|
|
′′ |
(x1 |
− h)+ y |
′′ |
(x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
(x1 |
− h)+ y |
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
(h)= |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
R |
|
3 |
|
y |
|
|
|
|
|
|
+ h) |
3 |
|
|
y |
|
|
(x1 + h) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
− |
h |
|
|
|
|
′′′ |
(x1 − h)+ y |
′′′ |
(x1 |
+ h) |
|
= − |
|
h |
|
|
|
′′′ |
(x1 − h)+ y |
′′′ |
(x1 |
|
+ h) |
|
= |
(6.6) |
|||||||||||||||||||||||||||||||||||||
|
|
|
3 |
−y |
|
|
|
|
|
|
|
3 |
− y |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
= − |
|
h2 yIV (ξ3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где ξ3 (x1 − h, x1 + h). |
|
R(0)= 0 ; |
|
R′(0)= 0 ; |
|
R′′(0)= 0 . Последовательно ин- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Кроме того, имеем |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тегрируя R′′′(h) |
и используя теорему о среднем, находим: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
R′′(h)= R′′(0)+ ∫h R′′′(t )dt = − |
2 |
|
∫h t 2 yIV (ξ3 )dt = − |
|
2 |
yIV (ξ2 )∫h t2dt = − |
2 |
h2 yIV (ξ2 ) |
(6.7) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
3 |
9 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где ξ2 (x1 − h, x1 + h). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
R′(h)= R′(0)+ ∫h R′′(t )dt = − |
|
2 |
|
∫h t3 yIV (ξ2 )dt = − |
|
2 |
yIV (ξ1 )∫h t 3dt = − |
|
1 |
|
h4 yIV (ξ1 ) |
(6.8) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
9 |
|
9 |
18 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
где ξ1 (x1 − h, x1 + h). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
R(h)= R(0)+ ∫h R′(t )dt = − |
|
1 |
|
∫h t4 yIV (ξ1 )dt = − |
1 |
|
|
yIV (ξ )∫h t4dt = − |
|
1 |
|
h5 yIV (ξ ) |
(6.9) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
18 |
|
18 |
|
90 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
где ξ (x1 − h, x1 + h). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Таким образом, остаточный член формулы Симпсона равен:
R = − |
h5 |
yIV (ξ ), где ξ (x0 , x2 ) |
(6.10) |
|
|||
90 |
|
|
|
44

Т.о. формула Симпсона более точная, чем формула трапеций.
Общая (обобщенная) формула Симпсона
|
|
|
Пусть n = 2 m |
есть четное число и yi |
= f (xi ) |
(i = 0,1,2,...,n) значения |
|||||||||||||||||||
функции |
|
y = f (x) |
для равноотстоящих точек |
a = x0 < x1 < x2 < ...< xn = b |
|
с |
|||||||||||||||||||
шагом h = b − a = b − a . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
2 m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применяя формулу Симпсона к каждому удвоенному промежутку x |
0 |
, x |
2 |
, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
2 |
, x |
|
... x |
2 m− |
2 |
,x |
|
длины 2 h получим: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
4 |
|
|
2 m |
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫b |
ydx ≈ h |
|
(y0 + 4 y1 + y2 )+ h |
(y2 + 4 y3 + y4 )+ |
...+ h |
(y2 m−2 + 4 y2 m−1 + y2 m ) |
|||||||||||||||||||
a |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
b |
|
|
Отсюда получаем общую (обобщенную) формулу Симпсона: |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ ydx ≈ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.11) |
||||||||
3 |
(y0 |
+ y2 m )+ 4 (y1 + y3 + ...+ y2 m−1 )+ 2 (y2 + y4 + ...+ y2 m−2 ) |
|||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Или: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
b |
|
|
|
|
h |
|
|
|
|
2 m−1 |
|
2 m−2 |
|
|
|
|
|
|
|
|
||
|
|
|
∫ ydx ≈ |
|
|
+ y2 m )+ 4 ∑ yi нечёт. |
+ 2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
(y0 |
∑ yi чёт. |
|
(6.12) |
|
|
||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
i=1 |
|
i=2 |
|
|
|
|
|
|
|
|
|||
b |
|
|
|
≈ h |
|
|
|
|
|
|
|
|
2 m−1 |
|
|
|
1, |
при i − нечёт. |
|
|
|
|
|
||
∫ ydx |
|
|
|
|
+ y2 m )+ ∑ (3 |
, где |
C = |
(6.13) |
|
|
|||||||||||||||
|
(y0 |
+ Ci ) yi |
|
|
при i − чёт. |
|
|
||||||||||||||||||
a |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
i=1 |
|
|
|
−1, |
|
|
|
|
|
||
Остаточный член общей формулы Симпсона равен сумме остаточных членов на каждом из m участков. Если ввести среднее значение четвертой произ-
водной yc IV (ξ ), то: |
|
|
|
|
R = − |
h5 |
yc IV (ξ )= −(b − a) |
h4 |
yc IV (ξ ) |
|
180 |
|||
90 |
|
|
||
Чаще эту формулу не применяют, а выполняют просчет с шагом Получаем:
(6.14)
h и 2 h .
R = −(b − a) |
h4 |
|
yIV |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
h |
|
|
180 |
|
|
|
R2h |
= 16 |
|
|
|
|
(6.15) |
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
(2 |
h)4 |
|
|
|
|
|
|
||||
R |
= −(b − a) |
|
yIV |
|
Rh |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
2h |
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
||
I = Ih + Rh |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ih + Rh = I |
2h + 16 Rh Rh = |
I |
h |
− I |
2h |
(6.16) |
||||||||||
|
|
|
|
|||||||||||||
I = |
|
|
15 |
|
||||||||||||
I2h + R2h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Формула (6.16) – проверка погрешности по Рунге. Пример расчета представлен на рис. 6.2
45
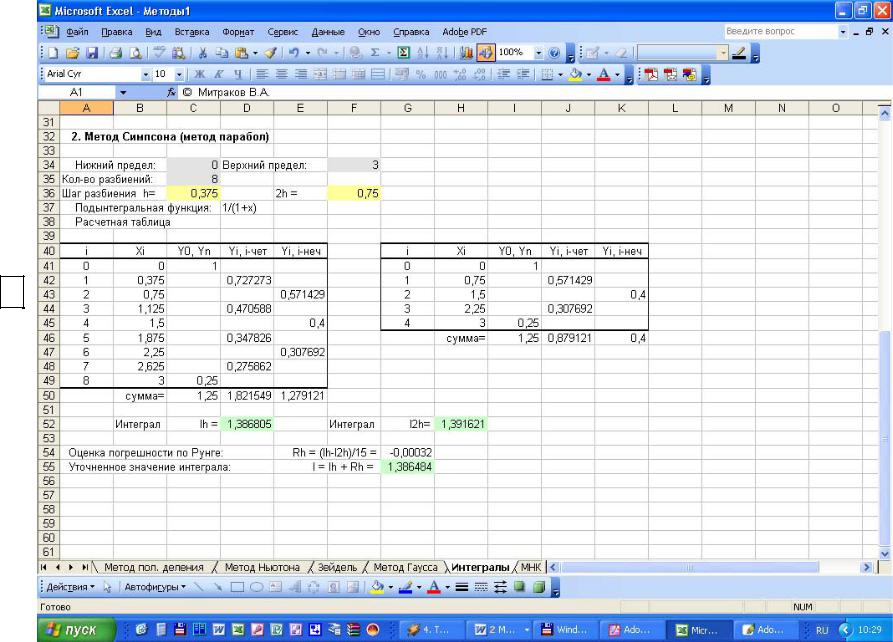
Рис. 6.2
Пример расчета по методу Симпсона в
Microsoft Excel
46
