Тогда:
a |
0 |
|
= A−1 B |
(8.13) |
|
|
|||
a1 |
|
|
|
|
Найденные параметры регрессии a0 , a1 подставляют в уравнение (8.8) и
таким образом получают эмпирическое линейное уравнение наилучшим образом описывающее экспериментальные данные.
Коэффициент линейной корреляции1
Для оценки соответствия подобранной прямой и экспериментальных данных вводят понятие коэффициента линейной корреляции, который вычисляется по формуле:
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
∑(xk − |
|
) (yk − |
|
) |
|
|
||||
|
|
|
|
|
|
|
Ryx |
|
x |
y |
||||||||||
|
|
|
|
|
|
|
= |
k=1 |
|
|
|
|
|
(8.14) |
||||||
|
|
|
|
|
|
|
N |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
N |
||||||||||
|
|
|
|
|
|
|
|
|
|
∑(xk − |
|
)2 |
∑(yk − |
|
)2 |
|
||||
|
|
|
|
|
|
|
|
|
|
x |
y |
|||||||||
|
|
|
|
|
|
|
|
|
|
k=1 |
k=1 |
|||||||||
где: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
N |
|
|
1 |
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
∑xk , |
|
= |
|
∑yk – средние величины переменных х и у. |
|||||||||||||
|
x |
y |
||||||||||||||||||
|
N |
|
||||||||||||||||||
|
|
|
k=1 |
|
|
N |
k=1 |
|
|
|
|
|
|
|
|
|
|
|
||
Коэффициент корреляции характеризует тесноту линейной зависимости и |
||||||||||||||||||||
принимает значения в интервале −1 ≤ Ryx |
≤ 1. Чем ближе Ryx к 1 или -1, тем |
|||||||||||||||||||
тесней линейная связь (прямая или обратная) между переменными х и у.
Квадратичная аппроксимация
При m = 2 получаем функцию:
f(x)= a0 + a1 x + a2 x2
Вэтом случае нормальная система имеет вид:
|
∂F (a0 , a1 ,a2 ) |
N |
||||||
|
= 2∑(a0 + a1 xk + a2 xk 2 − yk )= 0 |
|||||||
∂a0 |
|
|
|
|
||||
|
|
|
|
|
k=1 |
|||
|
∂F (a , a |
|
,a |
|
) |
N |
||
|
1 |
2 |
= 2∑(a0 + a1 xk + a2 xk 2 − yk ) xk = 0 |
|||||
|
0 |
|
|
|
||||
∂a1 |
|
|
|
|
||||
|
|
|
|
|
k=1 |
|||
|
∂F (a0 , a1 ,a2 ) |
N |
||||||
|
= 2∑(a0 + a1 xk + a2 xk 2 − yk ) xk 2 = 0 |
|||||||
∂a |
|
|
|
|
|
|||
|
2 |
|
|
|
|
k=1 |
||
|
|
|
|
|
|
|
||
(8.15)
(8.16)
После преобразования имеем нормальную систему трех уравнений относительно неизвестных параметров регрессии a0 , a1 , a2 .
1 Данный раздел предназначен для самостоятельного изучения
55
|
|
N |
N |
N |
|
a0 N + a1 ∑xk + a2 ∑xk2 = |
∑yk |
|
|||
|
|
k=1 |
k=1 |
k=1 |
|
|
N |
N |
N |
N |
|
a0 |
∑xk |
+ a1 ∑xk2 + a2 ∑xk3 = ∑xk yk |
(8.17) |
||
|
k=1 |
k=1 |
k=1 |
k=1 |
|
|
N |
N |
N |
N |
|
a0 |
∑xk2 + a1 ∑xk3 + a2 ∑xk4 = ∑xk2 yk |
|
|||
|
k=1 |
k=1 |
k=1 |
k=1 |
|
Решив систему (8.17) относительно параметров a0 , a1 , a2 получаем кон-
кретный вид функции (8.15). Изменение количества параметров не приведет к изменению сути самого подхода, а выразится в изменении количества уравнений в системе (8.17).
Значения разностей |
|
yk − F (a0 ,a1 ,a2 )= εk |
(8.18) |
называют отклонениями измеренных значений от вычисленных по формулам
(8.8) или (8.15).
Сумма квадратов отклонений
N |
|
σ = ∑εk2 |
(8.19) |
k=1
всоответствии с принципом наименьших квадратов для заданного вида при-
ближающей функции должна быть наименьшей.
Из двух разных приближений одной и той же табличной функции лучшим считается то, для которого (8.19) имеет наименьшее значение.
Аналогично можно записать систему для полинома любой степени m ≤ N :
f (x)= a0 + a1 x + a2 x2 + ...+ am xm |
(8.20) |
При этом, если m = N , то точечная средняя квадратичная аппроксимация алгебраическим многочленом совпадает с лагранжевой интерполяцией. Следовательно, повышение степени аппроксимирующего полинома на определенном шаге приведет к ухудшению качества и вызовет необходимость использовать аппроксимацию сплайнами. Другой путь повышения качества аппроксимации связан с выбором вместо алгебраических полиномов других ортогональных полиномов, а также функций вида:
y = a xb |
y = a bx |
y = a + |
b |
|
|||
x |
|||||||
|
|
|
|
|
|||
|
1 |
|
x |
|
(8.21) |
||
y = |
y = |
y = a lg x |
|||||
a x + b |
a x + b |
||||||
|
|
|
|
|
|||
и других, которые легко линеаризуются путем логарифмирования или замены переменных.
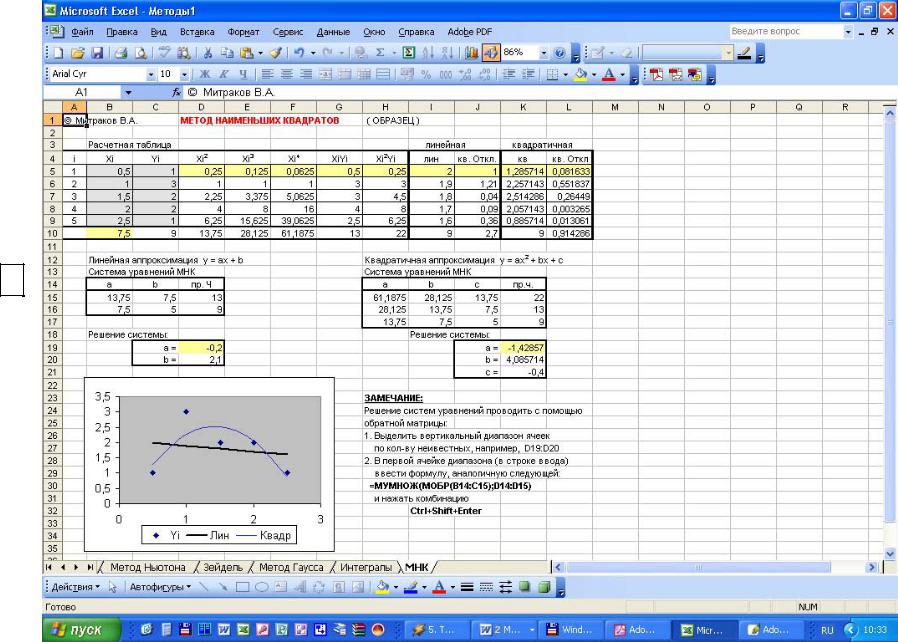
Пример реализации метода наименьших квадратов в среде Microsoft Excel представлен на рис. 8.2.
56
57
Рис. 8.2
Пример расчета по методу наименьших квадратов в
Microsoft Excel