Тема 3. Численное интегрирование
Лекция 5. Метод трапеций
Если функция f (x) непрерывна на отрезке [a,b] и известна ее первообразная F (x), то определенный интеграл от этой функции может быть вычис-
лен по формуле Ньютона-Лейбница: |
|
|
∫b |
f (x)dx = F (b)− F (a), |
(5.1) |
a
где F′(x)= f (x). Однако, во многих случаях, возникают большие трудности,
связанные с нахождением первообразной, или эта задача не может быть решена элементарными способами. Поэтому во многих случаях бывает затруднительно или невозможно применить формулу (5.1). Кроме того, подынтегральная функ-
ция f (x) часто бывает задана таблично. Поэтому численные методы вычисле-
ния интегралов имеют важное значение.
Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции.
Численное вычисление однократного интеграла называют механической квадратурой, а двойного – механической кубатурой. Соответствующие формулы называют квадратурными и кубатурными формулами.
Постановка задачи
Пусть требуется найти определенный интеграл |
|
|
F = ∫b |
f (x)ρ(x)dx , ρ(x)> 0 |
(5.2) |
a
где функция f (x) непрерывна на отрезке [a,b], а весовая функция ρ(x) непрерывна на интервале (a,b). Выразить интеграл через элементарные функции удается редко, а компактный и удобный для доведения до числа ответ получается еще реже. Поэтому обычно заменяют f (x) на такую аппроксимирующую функцию ϕ(x,a)≈ f (x), чтобы интеграл от нее вычислялся в элементарных функциях.
Чаще всего f (x) заменяют некоторым обобщенным интерполяционным
многочленом. Поскольку такая аппроксимация линейна относительно параметров, то функция при этом заменяется некоторым линейным выражением, коэффициентами которого служат значения функции в узлах:
n |
|
f (x)= ∑ f (xi ) ϕi (x)+ r (x) |
(5.3) |
i=0
где r (x) – остаточный член аппроксимации. Подставляя (5.3) в (5.2), получим формулу численного интегрирования (квадратурную формулу):
38
n |
(xi )+ R , |
F = ∑ci f |
|
i=0 |
(5.4) |
|
|
ci = ∫b ϕi (x) ρ(x)dx , |
R = ∫b r (x) ρ(x)dx |
a |
a |
где величины xi – называют узлами, ci |
– весами, а R – погрешностью или |
остаточным членом формулы. Интеграл приближенно заменяется суммой, похожей на интегральную сумму, причем узлы и коэффициенты этой суммы не
зависят от функции f (x). Интерполяционный многочлен (5.3) может быть не
только лагранжева, но и эрмитова типа; в последнем случае в сумму (5.4) войдут производные функции в узлах.
Лучше всего изучена замена функции f (x) алгебраическим многочленом, которую и рассмотрим ниже.
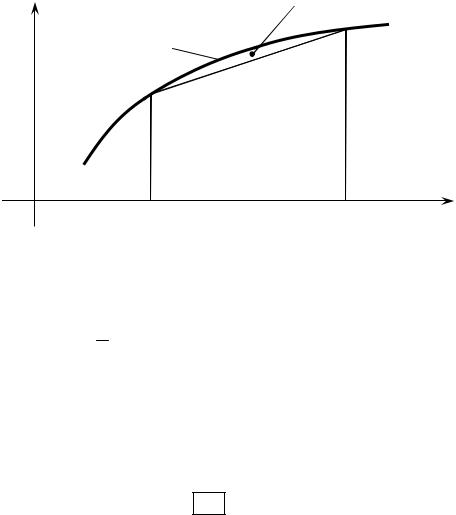
Формула трапеций
Геометрическая интерпретация определенного интеграла F = ∫b f (x)dx со-
a
стоит в том, что он численно равен площади криволинейной трапеции ограниченной частью оси абсцисс, двумя прямыми x = a , x = b и подынтегральной
кривой y = f (x) (рис. 5.1).
R
y = f (x)
a |
b |
Рис. 5.1 Геометрические построения для метода трапеций
Заменяя приближенно функцию f (x) линией, получим трапецию, пло-
щадь которой равна F 1 = 21 (b − a) ( f (a)+ f (b)), или
F = ∫b |
f (x)dx ≈ |
1 |
(b − a) ( f (a)+ f (b)). |
(5.5) |
|
2 |
|||||
a |
|
|
|
39
Формула (5.5) это формула трапеций для приближенного вычисления определенного интеграла. Ошибка квадратурной формулы – это площадь равная R . Найдем ее погрешность.
Погрешность формулы трапеций
Для этого разложим f (x) по формуле Тейлора, выбирая середину отрезка
за центр разложения и предполагая наличие у функции требуемых по ходу рассуждений непрерывных производных:
f (x)= f (x )+ (x − x ) f ′(x )+ 21 (x − x )2 f ′′(x )+ ...,
где |
x = |
1 |
(a + b) |
(5.6) |
|
2 |
|||||
|
|
|
|
Погрешность есть разность точного и приближенного значений интеграла. Подставляя в (5.5) разложение (5.6) получим главный член погрешности:
R = ∫b |
f (x)dx − b − a |
( f (a)+ f (b))≈ − |
1 |
(b − a)3 f ′′(x ), |
(5.7) |
|
|||||
a |
2 |
|
12 |
|
|
где члены, отброшенные при замене точного равенства приближенным, содержат старшие производные и более высокие степени длины отрезка интегриро-
вания. Заметим, что содержащие f (x ) и f ′(x )члены разложения (5.6) унич-
тожились и не дали вклада в погрешность; это было нетрудно предвидеть, ибо формула трапеций по самому выводу точна для многочлена первой степени.
Это же можно получить иным способом:
Предполагаем, что функция y = f (x) |
принадлежит |
|
y C(2) [a,b] и дваж- |
|||||||||||||||||||||||
ды дифференцируема. Будем рассматривать |
R = R(h) |
как |
функцию шага |
|||||||||||||||||||||||
h = x1 − x0 = b − a . Тогда можно положить |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
R(h)= |
x0 +h |
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
∫ |
ydx − |
|
|
|
|
|
|
|
|
|
|
|
|
(5.8) |
|||||||
|
|
|
|
|
2 |
y(x0 )+ y(x0 + h) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференцируем эту формулу два раза по h. |
|
|
|
|
|
|
|
|||||||||||||||||||
′ |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
− |
h |
|
′ |
(x0 |
+ h)= |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
R (h)= y(x0 + h)− |
2 |
y(x0 )+ y(x0 + h) |
2 |
y |
|
(5.9) |
||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x0 |
+ h) |
|
|
|
|
|
||||||
= |
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
y(x0 + h)− y(x0 ) |
− |
2 |
y |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R′′(h)= |
1 |
y′(x0 + h)− |
|
1 |
y′ |
(x0 + h)− |
h |
y′′(x0 |
+ h) |
= − h |
y′′(x0 + h) |
(5.10) |
||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
причем R(0)= 0 ; |
R′(0)= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Отсюда, интегрируя R′′(h) по h и используя теорему о среднем, получаем, |
||||||||||||||||||||||||||
последовательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
R′(h)= R′(0)+ ∫h R′′(t )dt = |
|
0 − |
1 |
∫h t y′′(x0 + t )dt = − |
|
1 |
y′′(ξ1 ) |
∫h tdt = − h2 |
y′′(ξ1 ), (5.11) |
|||||||||||||||||
|
|
2 |
||||||||||||||||||||||||
0 |
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
4 |
|
|||||
40
где ξ1 (x0 , x0 + h), отсюда:
R(h)= R(0)+ ∫h R′(t
0
где ξ (x0 , x0 + h),
)dt = 0 − 1 ∫h t y′′(x0 + t )dt
4 0
т.е:
R(h)= − 12h3 y′′(ξ )
= − |
1 |
y′′(ξ )∫h t2dt = − h3 |
y′′(ξ ), (5.12) |
||
4 |
|||||
|
0 |
12 |
|
||
|
|
|
|
(5.13) |
|
Знак разности указывает на то, что если вторая производная на отрезке положительна, то формула (5.5) аппроксимируется с избытком, в противном случае – с недостатком.
Общая формула трапеций
Вообще, длина отрезка b − a не мала, поэтому остаточный член (5.7) может быть велик. Для повышения точности на отрезке [a,b] вводят достаточно густую сетку a = x0 < x1 < x2 < ...< xn = b (разбивают отрезок на n частей). Ин-
теграл разбивают на сумму интегралов по шагам сетки и к каждому шагу при-
меняют формулу (5.5). Получают общую (обобщенную) формулу трапеций:
b |
1 |
n |
|
∫ f (x)dx ≈ |
∑(xi − xi−1 ) ( fi−1 + fi ), |
||
|
|||
a |
2 i=1 |
||
(5.14)
R ≈ − 1 ∑n (xi − xi−1 )3 f ′′(xi )
12 i=1
На равномерной сетке она упрощается:
b |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
∫ f (x)dx ≈ h |
|
f0 |
+ |
f1 + |
f2 + ...+ |
fn−1 + |
|
fn |
, |
||
2 |
2 |
||||||||||
a |
|
|
|
|
|
|
|
|
|||
|
|
|
|
(5.15) |
|
|
1 |
n |
1 |
b |
|
R ≈ − |
∑h3 f ′′(xi )≈ − |
h2 ∫ f ′′(x)dx , h = xi − xi−1 = const |
|||
12 |
12 |
||||
|
i=1 |
a |
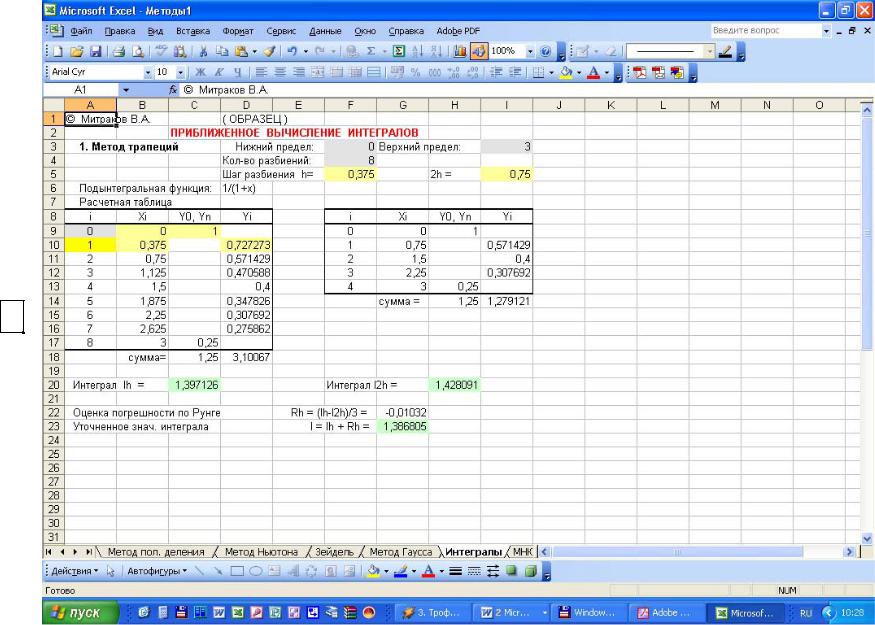
Пример расчета представлен на рис. 5.2
Формула (5.13) не всегда удобна при вычислениях, поэтому в большинстве случаев применяют оценку погрешности по методу Рунге:1:
R = |
Ih − I2h |
(5.16) |
|
3 |
|||
|
|
Где Ih и I2h - значения интеграла вычисленные на сетке с одинарным и двойным шагом разбиения соответственно.
1 Вывод данной формулы выносится на самостоятельное изучение.
41
42
Рис. 5.2 Пример расчета по методу трапе-
ций в Microsoft Excel