Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_1

.pdf

Скачиваний:

1052

Добавлен:

19.02.2016

Размер:

6.63 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2822 23 24 25 26 27 28 > Следующая >>>

Micromodule 18

BASIC THEORETICAL INFORMATION

DERIVATIVE AND ITS CALCULATION (CONTINUED)

Derivative of inverse function. Derivative of implicit function and function in parametric form. Logarithmic differentiation.

Literature: [3, chapter 3, §§ 3.1—3.8], [4, part 5], [6, chapter 5, § 2], [9], [10, chapter 4, § 5], [11, chapter 4, § 2], [12, chapter 3, §§ 16—18].

18.1. Derivative of inverse function

Let y = f (x) and x = g( y) be a pair of inter-inverse functions (remember,

that the plots of such functions coinside).

Let’s prove a theorem about connection between derivatives of these

functons.
	If functon y = f (x)			is monotone on the interval				(a; b) and
Theorem 3.10	If functon y = f (x)			is monotone on the interval				(a; b) and
	has non-zero derivative				f ′(x) at any point of this interval, then
there exists inverse function x = g( y), which has derivative x′ = g( y), and
	g′( y) =		1	,	or y′ =	1	.
		f	′(x)			x′
This formula has geometrical interpritation.
The curve is set by the function y = f (x)					or inverse function x = g( y)			(Fig. 3.15).

Then f ′(x) = tg α ( α is the angle between the tangent line and x-axis),

g′( y) = tg β

Then, tg α =

( β is the angle between the tangent line and y-axis). Since α + β =							π .
	π		1		1		2
tg (		− β) = ctgβ =		and y′ =		.

	2		tgβ		x′

y= f(x) x = g(x)

	M(x; y)
	α
О β	x

Fig. 3.15

211

	18.2. Differentiation of implicit function
Let the implicit function		y = f (x) is set by equation	F(x, y) = 0. In order
to find the	derivative y′(x) ,	we need to differentiate both parts of equation
F(x, y) = 0	with respect to	x , and not to forget that	y is	a function of
variable x . The obtained equation may be solved with respect to				′
				y (x) . So, we

find derivative from the condition

dxd F(x, y) = 0.

Derivative of implicit function is expressed through the independent variable x and function y itself.

18.3. Differentiation of functions given parametrically

The derivative of function y = f (x), given by parametrical equation x = x(t),

y = y(t) (where x(t) and y(t)			are differentiable at the point t and y′(t) = 0, is
found by the formula
	d			dy		ψ′(t) or y′			yt′
	d	=		dt	=	ψ′(t) or y′		=	yt′	.
	dx			dx		ϕ′(t)	x		xt′
				dt

18.4. Logarithmic differentiation

In some cases while finding derivative we should at first take the logarithm of given function and then find the derivative as in the case of implicit functon. This operation is called logarithmic differentiation.

It is particularly convenient to use logarithmic differentiation if the function is represented as:

а) y = u1k1 (x) u2k2 (x) … umkm (x) (x) ; b) or y = u(x)v(x) . v1l1 (x) v2l2 (x) … vmln (x) (x)

Let’s show how to find the derivative of the function y = u(x)v(x) , where

u(x), v(x) are differentiable functions with respect to						x, u(x) > 0 .
Applying the logarithm, we receive				1			1
ln y = ln(uv ) = v ln u ;	(ln y)′ = (v ln y)′ ;			1		y′ = v′ lnu + v	1	u′ ;
ln y = ln(uv ) = v ln u ;	(ln y)′ = (v ln y)′ ;				y	y′ = v′ lnu + v		u′ ;
					y		u
y′ = uv v′ ln u + v		1	u′ = uv ln u	v′ + vuv−1 u′
y′ = uv v′ ln u + v			u′ = uv ln u	v′ + vuv−1 u′
		u
212

Micromodule 18

EXAMPLES OF PROBLEMS SOLUTION

Example 1. Find the derivative	y′ , if		x = y3 + 3y .
Solution. We receive
x′ = 3y2 + 3 ; y′ =			1	=		1		.
x′ = 3y2 + 3 ; y′ =				=		2		.
		x	x′		3( y	2	+ 1)
			y		3( y		+ 1)
Example 2. Find the derivative	x′	, if	y = x + ex .
	y
Solution. The functon y = x + ex		is monotone for						x R. y′ = 1+ ex > 0 .

That is why for function y(x) there exists inverse functon x = x( y) and its

derivative is	x′ =	1	=		1	.
derivative is	x′ =		=	1+ ex		.
		y′		1+ ex
Example 3. Prove that							1
						(arcsin x)′ =	1	.
						(arcsin x)′ =	1− x2	.
							1− x2
Solution.	The function y = arcsin x						(where x [−1; 1] ), is inverse to

function x = sin y , y −π	2	, π	2	.
	2		2

x = sin y increases and the derivative theorem are fullfiled. We receive

(arcsin x)′ =	1	=
	cos y

On interval		−π	2	, π	2		the function
			2		2

x′ = cos y > 0. That is, all conditions of

1	=	1	.
1 − sin2 y		1 − x2

Example 4. Find the derivative y′, if x2 + y2 = 1.

Solution. We have 2x + 2yy′ = 0 , and we get y′ = − xy .

Example 5. Find the derivative y′, if x2 + 2xy − y2 = 2x.

Solution. Let’s differentiate both sides of equation with respect to х keeping in mind that у is a function of х:

2x + 2( y + xy′) − 2yy′ = 2 , or x + y + xy′ − yy′ = 1 .

We find y′(x − y) = 1− x − y. That is,	y′ =	1 − x − y .
		x − y

213

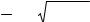
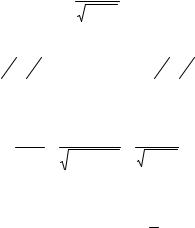
Example 6. Find

y′ , if

arctg

= ln

x2 + y2 .

Solution. We have

y ′

′

arctg

ln(x

+ y

)

+ y

) ,

y 2

(x2 + y2 )

y′ − y

2x + 2yy′

′x − y = x + yy′, y′(x − y) = x + y,

x2 + y2

2(x2 + y2 )

x + y

y′ =

x − y

Example 7. Find

′

, if

y = a sin t .

= b cos t

Solution. y′(t) = a cost ,

x′(t) = −b sin t , then

y′

a cos t

= −

ctg(t) .

− b sin t

Example 8. Find

′

, if

= t

− 2t

= 2t + t

Solution. Let’s find the derivatives

y′(t) = 2t − 6t 2 , x′(t) = 2 + 2t ,

then

y′

− 6t

− 3t

2 + 2t

1+ t

= arctg (t)

Example 9. Find

′

, if

x = ln (1+ t2 )

Soluton. We have

y′ =

x′(t) =

. Then

+ t 2

′

1+ t2

= 1+ t2

= 2t .

214


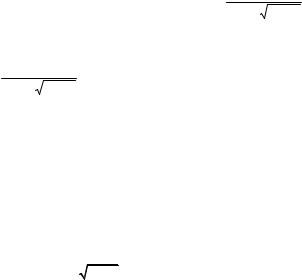
Example 10. Find the derivative of function	y =	x2	(3x − 2)ex
Example 10. Find the derivative of function	y =	sin x		.
		sin x		2x + 1

Solution. We use logarithmic differentiation and receive:

x2 (3x − 2)ex

;

ln y = 2 ln x + ln(3x − 2)+ x − ln sin x −

ln(2x + 1);

ln y = ln

sin x 2x + 1

ln y = 2 ln x + ln(3x − 2)+ x − ln sin x − 1 ln(2x + 1);

y′ =

+ 1−

cos x −

;

3x − 2

sin x

2x + 1

y′ = y

+ 1−

cos x −

3x − 2

sin x

2x + 1

y′ =

(3x −

2)ex

+ 1

− ctg x −

sin x 2x + 1

3x − 2

2x + 1

Example 11. Find the derivative of function y = xcos x .

Solution. First method. Let’s use logarithmic differentiation. We have

ln y = ln xcos x ;		ln y = cos x ln x;				(ln y)′ = (cos x ln x)′;
y′			1				1
	= − sin x ln x	+ cos x		;	y′ = y	− sin x ln x + cos x	x	.
y			x

That is,

y′ = x

cos x

− sin x ln x + cos x

Second method. Using basic logarithmic equality

aloga b = b,

let's write

the given function as

y = xcos x

= (eln x )cos x

= ecos xln x .

Then

y′ = (ecos xln x )′ = ecos xln x (cos x ln x)′ =

= e

cos xln x

− sin x ln x + cos x

= x

cos x

− sin x ln x + cos x

215

Micromodule 18

CLASS AND HOME ASSIGNMENT

Find dydx using the rule of differentiation of inverse function, if:

x = y2 +

y2 + 1 .

x = y ln y + sin y.

x = lg cos y + cos ln y.

x = earccos y .

Find the derivative

y′

of implicit functions:

5. 3x+y

= 3x −3y .

arctg

x2 + y2 .

7. x y = yx .

8. x

+ y

= 3xy .

=1.

Find the derivative

y′

of functions given parametrically:

10.

x = a cos2 t , y = b sin2 t .

11. x = t ,

y = 3 t .

12.

x =

3at

y =

3at2

13.

x = et ,

y = e2t .

+t3

1+t3

14. x = et

cos t ,

y = et

sin t .

15.

x = a(t −sin t) ,

y = a(1−cos t) .

16.

x = t2 ,

y =

−t .

17.

x = e2t

cos2 t ,

y = e2t

sin2 t .

18.

x = t cos t ,

y = t sin t .

19.

x =

cos3 t

, y =

sin3

cos 2t

Find the derivative

y′ , using logarithmic differentiation:

20.

y = (ln x)x .

21.

y = (2x +1)2x−1 .

22. y =

2x tg x 5 x

3x −4

23.

y = (x − 4)

x3 + 3 .

24.

y = (x5 +5

x )arctg x .

(x − 2)3 x

25.

y = xln x +(ln x)x .

26.

y = (sin x)cos x (cos x)sin xx .

27.

y = (x5 +5

x )arctg x .

28.

y = xxx .

216

Answers

	1.				y2 + 1			. 2.			1	. 5.			3x (1− 3y )			. 6.	x x2 + y2 + y	. 7.
	1.							. 2.			1	. 5.			3x (1− 3y )			. 6.		. 7.
		y(2			y2 + 1 + 1)					ln y +1+ cos y					3y (1+ 3x )				x − y x2 + y2
8.	y − x2			.	9.	− b2	x		. 10.		−b / a . 11.		2			.	12. t(2 − t3 ) . 13 2et . 14.
	y2 − x					a2	y					36		t			1 − 2t3
15 ctg		t	.		16.	2sin2 t + sin 2t .
15 ctg		2	.		16.	2sin2 t + sin 2t .
		2				2cos2 t − sin 2t

ln y − y / x ln x − x / y .

sin t + cost . cost − sin t

Micromodule 18

SELF-TEST ASSIGNMENT


18.1. Find the derivative				dy		of implicit function.

				dx
18.1.1. x2 y + y2 x = x3 y3 .							18.1.2. y = arctg x −arctg y .
18.1.3. sin(xy) = x2 + y2 .							18.1.4. y cos x = sin(x −y) .
18.1.5. 3x +3y = 3x+y .							18.1.6. x3 + y3 −4axy = 0 .
18.1.7. ln(x + y) + x2 y =1.							18.1.8. x sin y = x2 + y2 .
18.1.9. x = y3 −4 y +1.							18.1.10. sin x −cos y = x −y .
18.1.11. cos(xy) +sin(xy) = y .							18.1.12. ctg 2y = 2 ctg x .
18.1.13. y3 + x3 y + xy2 =1 .							18.1.14. x4 + y4 = x3 y3 .
18.1.15. y = x −arcsin y .							18.1.16. x3 y + y3 x = x −y2 .
18.1.17. x2 y2 +2xy + x3 = y3 .							18.1.18. sin(x + y) = x −y .
18.1.19. x3 + y4 x = x3 −2y .							18.1.20. x tg y − y tg x = yx .
18.1.21. x3 y −y3 x = (x −y)3 .							18.1.22. arctg(x + y) = x −y2 .
18.1.23. 5x −5y = 5x+y .							18.1.24. y sin x + x sin y = y .
18.1.25. 3y ln y = x2 ( y +5) .							18.1.26. y3 −5y +6ax = 0 .
18.1.27. x3 y2 +2x−y = y .							18.1.28. 3x+y +3x−y = y3 .
18.1.29. y = x +e1+xy .							18.1.30. arcsin(x / y) + yx = y .
18.2. Find the derivative			dy		of function given parametrically.

			dx				18.2.2. y =1/ cos2 t , x = ln tg t.
18.2.1.	y = arccost,	x = arcsin t.
18.2.3.	y = bsin3 t,	x = a cos3 t.					18.2.4. y =1/ sin2 t , x = ln ctg t.

217

1−t2

−t2

−t

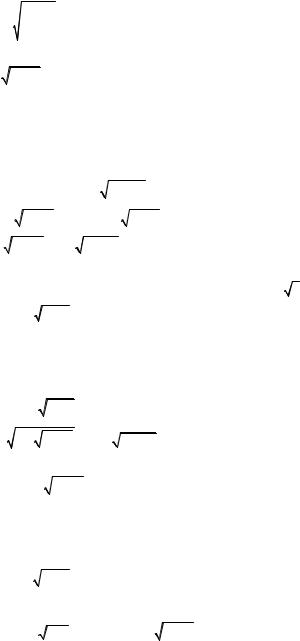
18.2.5. y = ln

, x = arctg t

18.2.6. y = e

= e

1+t2

18.2.7. y =

x = (arcsin t)2 .

18.2.8. y = et

sin t ,

x = et

cos t .

1−t2

18.2.9. y =

x = ln cos t .

18.2.10. y =

2at2

x =

sin

1+t3

+t3

18.2.11. y = a(1−cos 2t) ,

x = a(2t −sin 2t) .

18.2.12. y = a(sin t −t cos t) ,

x = a(t sin t +cos t) .

18.2.13. y = arcsin(t −1) , x =

2t −t2 .

18.2.14. y = t

t2 −1 , x = ln(t + t2 −1) .

18.2.15. y = 3 ln tg t , x =

arctg t .

18.2.16. y = t −arctgt , x = ln ctgt .

18.2.17. y =

cos t

, x = (1+cos t)2 .

18.2.18. y =

tg t

x =

ctg 2t

sin2 t

1−t2

18.2.19. y = ln

1−t2

18.2.20. y =

x =

, x =

ln2

+t2

1+t2

18.2.21. y = 2sin2 t + sin 2t ,

x = 3 tg 2t .

18.2.22. y = ln ctg et , x = tg(2e−t ) .

18.2.23. y = arcsin

1− t2 ,

x = arctg(t2 − 1) .

18.2.24. y = 1+ t2 −1 ,

x = 3 1−ln t .

18.2.25. y = arccos

x = arcsin

1+t2

18.2.26. y = t −arctg

, x = t3 −arcctg

18.2.27. y = (2 +3ln t) / t ,

x = a cos3 t .

18.2.28. y = arctg

1+ t2 ,

x = arccos1/ t2 .

18.2.29. y = tg3 2t + ctg3 2t ,

x = cos 2t −sin 2t .

18.2.30. y = arcsin

1− t ,

x = arccos 1−t2 .

218

18.3. Find the derivative dydx rentiation.

18.3.1. y = xarcsin x . 18.3.3. y = (x3 +1)sin x .

18.3.5. y = (sin x )1/ x . 18.3.7. y = (ctg 5x)5x−1 . 18.3.9. y = xe−tg x .

18.3.11. y = (x − 5)2 3 x2 + 1 . ex (x + 2)5

18.3.13. y = (x − 1)3 4 x2 + x .

4x (3x − 2)3

18.3.15. y = (x3 −x)x2 +1 . 18.3.17. y = xarctg x .

18.3.19. y = (x cos x)ln x . 18.3.21. y = (tg x)ctg x .

18.3.23. y = (cos x)tg x . 18.3.25. y = (4x −3)arccos x . 18.3.27. y = (ctg 2x)ctg x . 18.3.29. y = (5x +2)sin x .

of functions using the rule of logarithmic diffe-

18.3.2.	y = (lg x)x / 2 .
18.3.4.	y = (cos 2x)ln tg x / 2 .
18.3.6.	y = xex .
18.3.8.	y = (x5 +1)ctg x .
18.3.10.	y = (x8 + 1)tg x .

18.3.12.	y =	3x (2x − 1)(x + 1)4		.
		x(x −	3)6

18.3.14.	y =	2x (x − 5)(x + 1)3		.
		x(4x −	3)5

18.3.16. y = (2x −3)cos x .

18.3.18. y = (x sin x)x2 .

18.3.20. y = x2x . 18.3.22. y = (arcsin x)sin x .

18.3.24.y = x4x .

18.3.26.y = (ln(x +1))ln2 x .

18.3.28.y = xsin x +(sin x)x .

18.3.30. y = xarctg x .

Micromodule 19

BASIC THEORETICAL INFORMATION

DIFFERENTIAL OF FUNCTION. TANGENT

Differential of function. Geometrical interpretation of differential. The application of differentials in calculus of approximation. Tangent and normal.

Literature: [3, chapter 3, §§ 3.1—3.8], [4, section 4], [6, chapter 5, § 3], [7, chapter 6, § 17], [9], [10, chapter 4, § 14], [11, chapter 4, § 3], [12, chapter 3, §§ 20, 26].

219

19.1. Definition and geometrical interpretation of differential

Let function y = f (x) be differentiable at the point x, so that it has the derivative at this point:

f ' (x) = lim	y	.

x→0	x
In general case f ' (x) ≠ 0 . Then

yx = f ' (x) + α , where α → 0 if x → 0 , therefore the increment of the function is

y = f '(x) x + α x.

The first term is linear with respect to x , the second one is infinitesimal of the higher order than x . Therefore the first term forms the main part of the increment of function, which is called the differential of function.

Definition 3.21. The main, linear with respect to						x , part of the increment
of function	f (x) is called the differential dy of function y = f (x) :

			dy = f ′(x)		x .

Differential dy		is also termed		as the	first-order	differential or the first
differential.
If y = x	then	dy = dx = x' x =		x , so the differential of the independent

variable x is equal to its increment. Therefore:

dy = f ′(x)dx .

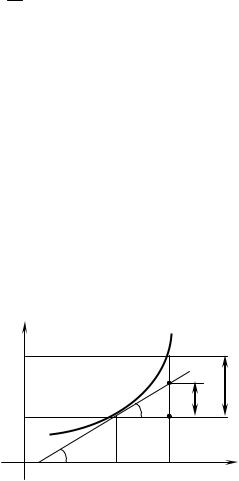
The geometrical interpretation of the differential is clear from Fig.3.16.

у
f(x + x)			P•
	y = f(x)		Q
	y = f(x)			у
			dу	у
	M	α	dу
	M
f(x)	•		N
	•	x	N

	α		A
О	x		x + x	х

Fig. 3.16

220

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2822 23 24 25 26 27 28 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.09.2019478.78 Кб6gtfnmТ.docx
#
15.08.2019637.53 Кб4Gulenko.docx
#
12.11.2018765.44 Кб6Hagakure_-_Sokrytoe_v_listve.doc
#
19.02.20166.95 Mб201Higher Mathematics. Part 3.pdf
#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf