Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_1

.pdf

Скачиваний:

1052

Добавлен:

19.02.2016

Размер:

6.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2813 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

9.3.27.

x −2

y −1

z +3

3x − y + 4z = 0 , P(−6; −3;

−2) .

−3

−2

9.1.28.

x −1

y +2

z −3

x + 2 y − 5z + 16 = 0 , P(1;

7) .

−2

−5

9.3.29.

x −1

y −3

z +2

3x − 7 y − 2z + 7 = 0 , P(2;

4; 8) .

−2

9.3.30.

x +3

y −2

z +5

5x + 7 y + 9z − 32 = 0 , P(7;

5; −3) .

−3

Micromodule 10

BASIC THEORETICAL INFORMATION

CURVES OF THE SECOND ORDER

Circle, an ellipse, a hyperbola: definition, equations in standard form, an eccentricity, directrices and their geometrical sense, hyperbola asymptotes. Parabola: definition, an equation in standard form, a parameter and a directrix of a parabola.

Literature: [1, chapter 7], [4, section 3, item 3.4], [6, chapter 3, § 6], [7,chapter 3, § 8], [10, chapter 2, § 5], [11, chapter 2, § 1].

10.1. Curves of the second order

A set of points in a plane whose coordinates satisfy the equation ax2 +by2 +cxy +dx +ey + f = 0

is called a second order curve provided at least one of numbers a, b, c is other

from zero. A circle, an ellipse, a hyperbola and a parabola belong to curves of the second order.

A set of points on a plane, whose distances from a given point of the plane (a center) are equal to a constant value (radius) is called a circle.

The equation

(x −a)2 +( y −b)2 = R2

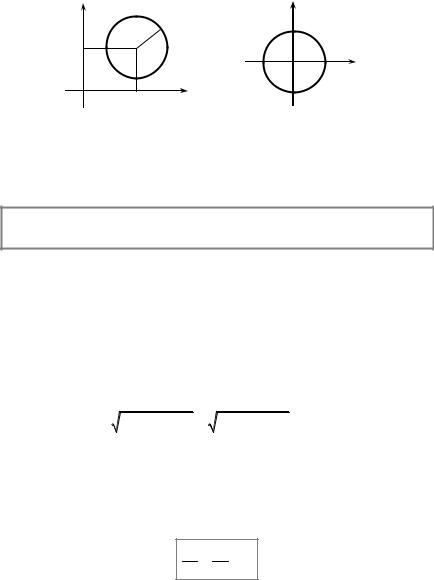
describes a circle of radius R. The center of the circle is at a point К(а,b) (Fig.2.19). If a circle center is located at the origin of coordinates (Fig.2.20), the equation of a circle has so called standard form.

x 2 + y 2 = R 2 .

121

y		y
	R	R
	R

b K

O R x

O	а	x
	Fig. 2.19	Fig. 2.20

10.2. Ellipse

An ellipse is a locus of all points in a plane whose sum of distances from two fixed points (foci) has a constant magnitude denoted as 2a (Fig.2.21).

Let us consider two points F1 and F2 (foci of an ellipse) in a plane.

We arrange coordinate axes so that the axis Ox passes through given points, and the axis Оу passes through a midpoint of the line segment F1 F2 per-

pendicularly to Ox. We denote a distance between foci as F1 F2 = 2c , and the sum of distances from any point of the ellipse to its foci as 2a, 2a > 2c. Then foci will have coordinates F1(−c, 0) and F2 (c, 0) .

According to the definition, any point M (x, y) lies on the ellipse if and only if the following equality holds

(x +c)2 + y2 + (x −c)2 + y2 = 2a .

When we square twice the left and right parts of this equation, we receive

x2 (a2 −c2 ) + y2 a2 = a2 (a2 −c2 ) .

Let us denote a difference a2 −c2 = b2 . Then x2b2 + y2 a2 = a2b2

x2 + y2 =1. a2 b2

The latter is called an equation of an ellipse in standard form.

Line segments A1 A2 = 2a and B1 B2 = 2b are called major and minor axes of the ellipse.

122

If a = b , the equation looks as x2 + y2 = a2 . So a circle is a particu-

lar case of an ellipse whose foci coincide at the same point called the center.

The measure of ellipse deviation from a circle is characterized by the

value ε = ac , 0 < ε < 1 and is called an

eccentricity of an ellipse.

Line segments F1M and F2 M are called focal radii of a point М:

x = − a	y		x = a
x = − a			x = a
ε	B1		ε
d1	B1	M	d2
A1	r1	r2	A2
		r2
	О
F1	О	F2	x
	B2

Fig. 2.21

r = F M =		(x +c)2 + y2 and			r	= F M = (x −c)2	+ y2 .
1	1				2	2
Straight lines		x = ± a	, or	x = ± a2	are called directrices of an ellipse.
		ε		c

Inasmuch as 0 < ε < 1, then ac2 > a, i.e. directrices of an ellipse lie outside of it.

The following statement is true for directrices.

The ratio of a focal radius of any point of an ellipse to the distance of this point to the corresponding directrix is a constant magnitude equal to the ellipse eccentricity, that is,

r1 = r2 = ε. d1 d2

10.3. Hyperbola

A hyperbola is a locus of all points in a plane a difference module of whose distances from two fixed points (foci) has a constant magnitude denoted as 2a (Fig. 2.22).

Let us denote a distance between foci F1F2 = 2c, and a module of difference of distances from any point of hyperbola to its foci as 2a, 2a < 2c. Then the foci will have coordinates F1(−c, 0) and F2 (c, 0).

By definition, any point M (x, y) lies on a hyperbola if and only if the following equality holds

(x +c)2 + y2 − (x −c)2 + y2 = 2a.

123

After some transformations we can get a standard equation of the hyperbola

	x2	−	y2	=1,
	a2	−	b2	=1,
	a2		b2
where b2 = c2 −a2.
A hyperbola consists of two branches and has two asymptotes whose
equations are y = ± b x.
a		y
		y
					d2
				d1
		r1			r2
					r2
					A2
F1	A1				F2	x
	x= –	a		x=	a
	x= –	ε		x=	ε

Fig. 2.22

A line segment A1 A2 = 2a is called a real axis of a hyperbola, а line segment B1 B2 = 2b is called an imaginary axis.

The equation		y2		−	x2	=1 determines a hyperbola called conjugate to the
		b2			a2

given hyperbola		x2	−		y2	=1 .
	a2				b2

A hyperbola eccentricity is determined by the ratio of a focal distance of a

hyperbola to the length of its real axis:
		ε =	c	, ε > 1.
	x = ± a	ε =	a	, ε > 1.
			a
Straight lines		, where a		is a real semi-axis of the hyperbola, are
	ε

called directrices of the hyperbola. They have the same property as directrices of an ellipse:

r1 = r2 = ε. d1 d2

124

10.4. Parabola

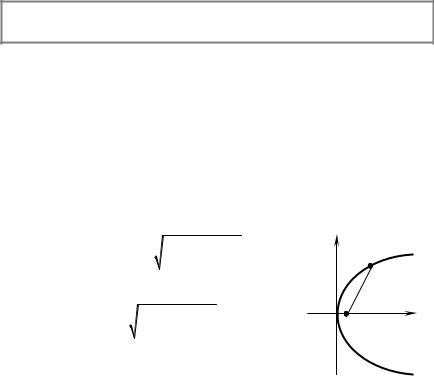
A parabola is a set of all points of a plane, equidistant from a given point (a focus) and a given straight line (a directrix) (Fig. 2.23).

Let us write down an equation of a parabola.

A focus F and a directrix are given on a plane and distance between them is equal to p. We can choose an axis Ox so that it would pass through the focus perpendicularly to the directrix, and an axis Оу would halve the distance between the focus and the directrix.

In the chosen

coordinate

system

the focus is

a point

, 0) , and a

directrix equation is

x = −

Any point M (x,

y) lies on a parabola if and only if the following equality

holds MB = MF , where

MB = x +

MF = (x −

+ y

)

Then

x +

= (x −

2 )

+ y

F (

; 0)

whence after some transformations we get a stan-

y2 = 2px

dard equation of the parabola

x= –

y2 = 2 px.

Fig. 2.23

An axis of parabola symmetry is called an axis of parabola. An intersection point of parabola with its axis is called a vertex of parabola. The number p equal to the distance between its focus and directrix is called a parameter of the parabola.

The parameter of a parabola characterizes the width of the area bounded by the parabola (the greater is p the wider the parabola is).

Micromodule 10

EXAMPLES OF PROBLEMS SOLUTION

Example 1. An equation of the second order curve is given 4x2 −5y2 +20 =0.

Determine a type of the curve, find its foci, semi-axes, an eccentricity, equations of directrices and asymptotes (for a hyperbola). Sketch its graph.

125

Solution. The given equation is reduced to a standard form

x2	−	y2	= −1 , or −	x2	+	y2	=1.
5		4		5		4

It is a conjugate hyperbola with a real semi-axis b = 2, lying on the axis Оу

and an imaginary semi-axis a = 5 on the axis Ох. A half of focal distance may be found from the condition

c2 = a2 + b2 = 9; c = 3.

Foci F1 і F2 lie on the axis Оу and have coordinates (0; –3) and (0; 3). The eccentricity is ε = bc , so ε =1,5.

Equations of directrices are y = ± bε , or y = ± 4 / 3.

Equations of asymptotes are y = ± ba x, or y = ± 25 x. A graph of the hyperbola is given in Fig. 2.24.

	y	l1
	F2	l1
	F2
	2	D2
		D2
–√5	√5	D1	x
	–2	l2
	F1	l2

Fig. 2.24

Example 2. Determine the type of a curve 4x2 + y2 + 8x − 2 y + 1 = 0, reduce

the equation to the simplest form, sketch the graph of the equation. Solution. Having completed perfect squares in х and y, we get

4(x2 + 2x) + ( y2 − 2y + 1) = 0 , 4(x2 + 2x + 1) + ( y2 − 2y + 1) = 4 ,

4(x + 1)	2	+ ( y − 1)	2	= 4 , (x + 1)	2	+	( y − 1)2	= 1 .
4(x + 1)		+ ( y − 1)		= 4 , (x + 1)		+	4	= 1 .
							4

126

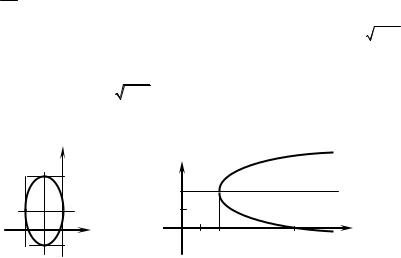
We have received an equation of the ellipse, that follows from an ellipse

x2 + y2 =1 by parallel displacement along the vector (–1; 1) (Fig. 2.25). 4

Example 3. Determine, what line is defined by the equation y = 2 − x − 2 and sketch its graph..

Solution. It is obvious, that x ≥ 2 and y < 2. At such restrictions we carry out transformations: y − 2 = − x − 2 , ( y − 2)2 = x − 2. The graph of the given equation is the lower branch of a parabola represented in Fig. 2.26.

3у

–1
–1 х	2	6	х
Fig. 2.25		Fig. 2.26

Micromodule 10

CLASS AND HOME ASSIGNMENT

1.Write down an equation of the ellipse whose foci are placed on the axis Ox symmetrically relative to the coordinate origin if its minor axis is equal to 24, and the distance between its foci is 2c =10.

2.Write down equations of a hyperbola whose foci are placed on the axis Ox symmetrically relative to the coordinate origin if a distance between its foci is 2c = 6 and its eccentricity is ε = 1,5.

3. Find a vertex and a parameter р of a parabola x = 4y2 − 8y + 7.

4.	Determine a type of a curve 4x2 − 32x − y2 + 2y + 59 = 0 and sketch its
graph.
		x2			y2				Answers
1.		x2	+		y2	=1. 3.	p =	1	, (3; 1) is a vertex of the parabola. 4. A hy-
1.	169		+	144		=1. 3.	p =	8	, (3; 1) is a vertex of the parabola. 4. A hy-
	169			144				8

perbola.

127

Micromodule 10

SELF-TEST ASSIGMENTS

10.1. Equation of a second order curve is given. Perform such operations: а) determine its type using an equation of the curve;

b)in case of an ellipse find lengths of its semi-axes, coordinates of its foci, an eccentricity , write down equations of directrices;

c)in case of a hyperbola find lengths of its semi-axes, coordinates of its foci, an eccentricity , write down equations of directrices and asymptotes;

d)in case of a parabola find a value of its parameter, coordinates of its focus, write down an equation of its directrix;

e)sketch the graph of the curve with representation of foci, directrices and asymptotes (if it is possible).

10.1.1. x2 + 4 y2 − 4 = 0.		10.1.2. 9x2 +4 y2 −36 = 0.
10.1.3. 16x2	− 25y2 − 400 = 0.	10.1.4. −16x2 + 25y2 −400 = 0.
10.1.5. x2 +10 y =10.		10.1.6.	9x2 −16y2 +144 = 0.
10.1.7. 16x2	+25y2 −400 = 0.	10.1.8.	y2 −4x = 4.

10.1.9.16x2 −36y2 −576 = 0. 10.1.10. 25x2 +16 y2 −400 = 0.

10.1.11.x2 −4y2 −4 = 0. 10.1.12. 4x2 + 25y2 −100 = 0.

10.1.13. 9x2		−36 y2 +324 = 0.	10.1.14. 4x2 +9 y2 −36 = 0.
10.1.15.	5x2	+ 4 y2 −20 = 0.	10.1.16.	25x2 +4 y2 −100 = 0.
10.1.17.	y2 +8x =16.		10.1.18.	16x2 −9y2 +144 = 0.

10.1.19.x2 +9 y2 −9 = 0. 10.1.20. 25x2 −36y2 −900 = 0.

10.1.21.9x2 −4y2 −36 = 0. 10.1.22. 4x2 −9 y2 +36 = 0.

10.1.23. x2 −12 y = 24.			10.1.24. 36x2 +16 y2 −576 = 0.
10.1.25. 9x2		+16y2 −144 = 0.	10.1.26. 5x2 −4 y2 +20 = 0.
10.1.27.	9x2	+36y2 −324 = 0.	10.1.28. x2 −4y2 + 4 = 0.
10.1.29.	36x2 +25y2 −900 = 0.		10.1.30. 25x2 −36y2 +900 = 0.

10.2.Distinguish, what line is defined by the equation and sketch its graph.

10.2.1.	y =1+	3	16−x2 .	10.2.2.	y = 2−	4		9−x2 .
		4				3

10.2.3.	y =1−	2	25−x2 .	10.2.4.	y = −2−		5	9−x2 .
		5					3

128

10.2.5. x =1+		2						9−y2 .			10.2.6. x = 2−			5			16−y2 .
10.2.5. x =1+		3						9−y2 .			10.2.6. x = 2−			4			16−y2 .
		3												4
10.2.7. x = 3+		7							4−y2 .		10.2.8. x = 3−			3			49−y2 .
10.2.7. x = 3+		2							4−y2 .		10.2.8. x = 3−			7			49−y2 .
		2												7
10.2.9. y = −1+						3				16 + x2 .	10.2.10. y = 2−				3			25+ x2 .
			4											5
10.2.11. y =	5				37 + x2 +2x .						10.2.12. y = −			6			29 +4x + x2 .
10.2.11. y =	6				37 + x2 +2x .						10.2.12. y = −			5			29 +4x + x2 .
	6													5
10.2.13. y =	4				50−2x + x2 .						10.2.14. y = −			7			20−4x + x2 .
10.2.13. y =	7				50−2x + x2 .						10.2.14. y = −			4			20−4x + x2 .
	7													4
10.2.15. y +1=			4						81+ x2 .		10.2.16. y −2 = −						9	25 + x2 .
10.2.15. y +1=			9						81+ x2 .		10.2.16. y −2 = −					5		25 + x2 .
			9													5
10.2.17. x =	7		5−2y + y2								10.2.18. x = −			3		53+4y + y2 .
10.2.17. x =	2		5−2y + y2								10.2.18. x = −			7		53+4y + y2 .
	2													7
10.2.19. x =	7				25+6y + y2 .						10.2.20. x =	8		25−16y + y2 .
	4										3
10.2.21. x −2 = −									5	49 + y2 .	10.2.22. x +1= −					4		9 + y2 .
10.2.21. x −2 = −								7		49 + y2 .	10.2.22. x +1= −					3		9 + y2 .
								7								3
10.2.23. y =1−3								1−x2 .			10.2.24. x +3 = −2							4−y2 .
10.2.25. y −1 =			5						9−x2 .		10.2.26. y = −			3		24−2x −x2 .
10.2.25. y −1 =			3						9−x2 .		10.2.26. y = −			5		24−2x −x2 .
			3											5
10.2.27. x −2 =				9						49 + y2 .	10.2.28. x +1= −					7		81+ y2 .
10.2.27. x −2 =			7							49 + y2 .	10.2.28. x +1= −					9		81+ y2 .
			7													9
10.2.29. x = −		7					80−2 y −y2 .				10.2.30. y =		2		26 +2x + x2 .
10.2.29. x = −		9					80−2 y −y2 .				10.2.30. y =				26 +2x + x2 .
		9									5

Micromodule 11

BASIC THEORETICAL INFORMATION

SURFACES OF THE SECOND ORDER

Cylindrical surfaces. Conic surface. A sphere. An ellipsoid. Hyperboloids of one and two sheets. An elliptic and hyperbolic paraboloid.

Literature: [1, chapter 7], [4, section 3, item 3.4], [6, chapter 3, §7], [7, chapter 3, §9], [10, chapter 2, §6].

129

11.1. General equation of a second order surface

A set of points whose coordinates satisfy the equation

ax2 +by2 +cz2 +dxy +exz + fyz + gx +hy +kz +l = 0 ,

is called a surface of the second order, where at least one of coefficients a, b, c, d, e, f is other than zero. Such an equation is called a general equa-

tion of a surface of the second order.

As a geometrical object a surface of the second order will not change after transition from one coordinate system to another. There exists a system of coordinates in which the equation of a surface has the simplest (standard) form.

Cylindrical, conic surfaces, rotating surfaces, a sphere, an ellipsoid, hyperboloid of one and two sheets, an elliptic and hyperbolic paraboloid are referred to the surfaces of the second order.

11.2. Cylindrical surfaces

The surface is called cylindrical if it is formed by a set of parallel straight lines (generatrices) intersecting the given line L (directrix).

The cylindrical surfaces whose directrices lie in a coordinate plane and generatrices are parallel to the coordinate axis perpendicular to that coordinate plane are considered most often. In this case an equation of the cylinder coincides with the equation of its directrix. For example, the equation

f (x, y) = 0

decribes a cylindrical surface whose directrix lies in the plane Оху and generatrices are parallel to the axis Oz .

Cylindrical surfaces whose directrices are curves of the second order are called cylindrical surfaces of the second order. Their standard equations are:

10. A circular cylinder			x2 + y2 = R2 .
2	0	. An elliptic cylinder	x2		+	y2		=1 (Fig. 2.27).
			a2			b2

3	0	. A hyperbolic cylinder		x2		−	y2		=1 (Fig. 2.28).
				a2			b2

40. A parabolic cylinder y2 = 2 px (Fig. 2.29).

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2813 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.09.2019478.78 Кб6gtfnmТ.docx
#
15.08.2019637.53 Кб2Gulenko.docx
#
12.11.2018765.44 Кб6Hagakure_-_Sokrytoe_v_listve.doc
#
19.02.20166.95 Mб201Higher Mathematics. Part 3.pdf
#
19.02.20169 Mб94Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20167.48 Mб407Higher_Mathematics_Part_2.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб10HiraganaKatakanaWorkSheet (1).pdf